Lớp 12 Toán 12 - Kết nối tri thức

Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 2

Mô tả thêm: Đề thi giữa HK1 Toán 12 được biên soạn bám sát chương trình sách kết nối tri thức giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức
  • Thời gian làm: 90 phút
  • Số câu hỏi: 22 câu
  • Số điểm tối đa: 22 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Trong các hàm số sau, hàm số nào đồng biến trên tập số thực?

    Xét hàm số y = x^{3} + x có: y' = 3x^{2} + 1 > 0;\forall x\mathbb{\in R}

    Suy ra hàm số y = x^{3} + x đồng biến trên tập số thực.

  • Câu 2: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Hàm số y = f(x) nghịch biến trên khoảng nào dưới dây?

    Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên (0;1).

  • Câu 3: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Mệnh đề nào sau đây đúng?

    Dựa vào bảng biến thiên ta suy ra mệnh đề đúng là: “Điểm cực tiểu của đồ thị hàm số là B(0;1)”.

  • Câu 4: Nhận biết

    Cho hàm số y = f(x) có đạo hàm f'(x) = x(x + 1)(x - 2)^{3};\forall x\mathbb{\in R}. Số điểm cực tiểu của hàm số là:

    Ta có: f'(x) = x(x + 1)(x - 2)^{3} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = - 1 \\ x = 2 \\ \end{matrix} ight.

    Bảng xét dấu:

    Suy ra số điểm cực tiểu của hàm số là 2 điểm.

  • Câu 5: Nhận biết

    Các đường tiệm cận của đồ thị hàm số y = \frac{2x + 1}{x - 3} tạo với hai trục tọa độ diện tích bằng bao nhiêu?

    Ta có: Đồ thị hàm số y = \frac{2x + 1}{x - 3} có đường tiệm cận đứng là x = 3 và đường tiệm cận ngang là y = 2

    Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có chiều dài và chiều rộng lần lượt là 3;2 nên diện tích của hình chữ nhật là S = 2.3 = 6.

  • Câu 6: Nhận biết

    Với giá trị nào của tham số m để đồ thị hàm số y = \frac{2x^{2} + 6mx + 4}{mx + 2} đi qua điểm A( - 1;4)?

    Thay tọa độ điểm A( - 1;4) vào y = \frac{2x^{2} + 6mx + 4}{mx + 2} ta được:

    4 = \frac{2.( - 1)^{2} + 6m.( - 1) + 4}{m.( - 1) + 2} \Leftrightarrow 2m = - 2 \Leftrightarrow m = - 1

    Vậy giá trị m cần tìm là m = - 1.

  • Câu 7: Nhận biết

    Cho hình vẽ:

    Đồ thị trong hình đã cho là đồ thị của hàm số nào?

    Từ đồ thị ta thấy đây là đồ thị hàm số bậc ba có dạng y = ax^{3} + bx^{2} + cx + d với a > 0 và đồ thị hàm số đi qua điểm (2; - 3) nên hàm số tương ứng với đồ thị trong hình vẽ đã cho là y = x^{3} -3x^{2} + 1.

  • Câu 8: Nhận biết

    Cho bốn điểm A;B;C;D trong không gian. Hỏi có bao nhiêu vectơ khác \overrightarrow{0} có điểm đầu và điểm cuối là 4 điểm?

    Lấy A làm gốc ta được 3 vectơ \overrightarrow{AB};\overrightarrow{AC};\overrightarrow{AD}. Tương tự đối với B;C;D ta được 4.3 = 12 vectơ.

  • Câu 9: Nhận biết

    Mệnh đề nào sau đây sai?

    Hai vectơ có độ dài bằng nhau và cùng hướng thì hai vectơ đó bằng nhau.

  • Câu 10: Thông hiểu

    Tìm điều kiện của tham số m để hàm số y = x^{4} + mx^{2} + c có ba điểm cực trị?

    Hàm số y = ax^{4} + bx^{2} + c có ba điểm cực trị khi và chỉ khi a.b < 0.

    Để hàm số đa cho có ba điểm cực trị khi và chỉ khi b < 0.

  • Câu 11: Thông hiểu

    Hỏi đồ thị hàm số y = \frac{x^{2} - \sqrt{2 - x}}{x - 1} - x có tất cả bao nhiêu đường tiệm cận?

    Tập xác định D = ( - \infty;2)\backslash\left\{ 1 ight\}

    Ta có:

    \lim_{x ightarrow - \infty}\left( \frac{x^{2} - \sqrt{2 - x}}{x - 1} - x ight) = \lim_{x ightarrow - \infty}\frac{x^{2} - \sqrt{2 - x}}{x - 1}

    = \lim_{x ightarrow -\infty}\dfrac{x\left( 1 + \sqrt{\dfrac{2}{x^{2}} - \dfrac{1}{x}}ight)}{x\left( 1 - \dfrac{1}{x} ight)} = \lim_{x ightarrow -\infty}\dfrac{1 + \sqrt{\dfrac{2}{x^{2}} - \dfrac{1}{x}}}{1 - \dfrac{1}{x}}= 1

    Suy ra y = 1 là tiệm cận ngang của đồ thị hàm số.

    \lim_{x ightarrow 1}\left( \frac{x^{2} - \sqrt{2 - x}}{x - 1} - x ight) = \lim_{x ightarrow 1}\frac{x^{2} - \sqrt{2 - x}}{x - 1}

    = \lim_{x ightarrow 1}\frac{x^{2} - 2 + x}{(x - 1)\left( x + \sqrt{2 - x} ight)} = \lim_{x ightarrow 1}\frac{x + 2}{x + \sqrt{2 - x}} = \frac{3}{2}

    Suy ra hàm số không có tiệm cận đứng

    Vậy hàm số có 1 đường tiệm cận.

  • Câu 12: Thông hiểu

    Cho hàm số y = \frac{{ax + b}}{{cx + d}} có bảng biến thiên như hình vẽ. Hỏi hàm số đã cho là hàm số nào?

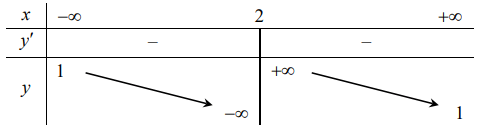
    Hàm số đã cho là hàm số nào

    Dựa vào bảng biến thiên ta thấy:

    Đồ thị hàm số nhận các đường thẳng x = 2 và tiệm cận ngang y = 1

    => Loại đáp án C và D

    Hàm số đã cho nghịch biến trên mỗi khoảng xác định

    Xét hàm số y = \frac{{x - 3}}{{x - 2}} \Rightarrow y' = \frac{1}{{{{\left( {x - 2} ight)}^2}}}

    => Hàm số đồng biến trên mỗi khoảng xác định nên ta loại đáp án A

  • Câu 13: Thông hiểu

    Trong không gian Oxyz , cho vectơ \overrightarrow{OA} = (2; - 1;5),B(5; - 5;7). Xét sự đúng sai của các khẳng định sau:

    a) Tọa độ của điểm A là (2; - 1;5). Đúng||Sai

    b) Gọi C(a;b;c) thỏa mãn ∆ABC nhận G(1;1;1) làm trọng tâm. Khi đó a + b + c = - 4 . Đúng||Sai

    c) Nếu A;B;M(x;y;1) thẳng hàng thì tổng x + y = 3 . Đúng||Sai

    d) Cho N \in (Oxy) để ∆ABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3. Sai||Đúng

    Đáp án là:

    Trong không gian Oxyz , cho vectơ \overrightarrow{OA} = (2; - 1;5),B(5; - 5;7). Xét sự đúng sai của các khẳng định sau:

    a) Tọa độ của điểm A là (2; - 1;5). Đúng||Sai

    b) Gọi C(a;b;c) thỏa mãn ∆ABC nhận G(1;1;1) làm trọng tâm. Khi đó a + b + c = - 4 . Đúng||Sai

    c) Nếu A;B;M(x;y;1) thẳng hàng thì tổng x + y = 3 . Đúng||Sai

    d) Cho N \in (Oxy) để ∆ABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3. Sai||Đúng

    a) Ta có:

    Tọa độ của điểm A là (2; - 1;5).

    b) G là trọng tâm tam giác ABC

    \Leftrightarrow \left\{ \begin{matrix}1 = \dfrac{2 + 5 + x_{C}}{3} \\1 = \dfrac{- 1 - 5 + y_{C}}{3} \\1 = \dfrac{5 + 7 + x_{C}}{3} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x_{C} = - 4 \\y_{C} = 9 \\x_{C} = - 9 \\\end{matrix} ight.\ \Rightarrow C( - 4;9; - 9)

    \Rightarrow a + b + c = - 4

    c) Ta có: \overrightarrow{AB} = (3; - 4;2);\overrightarrow{AC} = (x - 2;y + 1; - 4)

    Ba điểm A, B, M thằng hàng khi và chỉ khi

    \overrightarrow{AM} = k\overrightarrow{AB} \Leftrightarrow \left\{ \begin{matrix} x - 2 = 3k \\ y + 1 = k.( - 4) \\ - 4 = k.2 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = - 4 \\ y = 7 \\ k = - 2 \\ \end{matrix} ight.

    Suy ra x + y = 3

    d) Ta có: N \in (Oxy) \Rightarrow N = (x;y;0)

    \Rightarrow \overrightarrow{AN} = (x - 2;y + 1; - 5),\overrightarrow{AB} = (3; - 4;2)

    Ta có ∆ABN vuông cân tại A \Leftrightarrow \left\{ \begin{matrix} AN\bot AB(*) \\ AN = AB(**) \\ \end{matrix} ight.

    Từ (*) \Leftrightarrow \overrightarrow{AN}\bot\overrightarrow{AB} \Leftrightarrow 3(x - 2) - 4(y + 1) - 10 = 0

    \Leftrightarrow 3x - 4y = 20 \Leftrightarrow y = \frac{3}{4}x - 5

    Từ (**) AN^{2} = AB^{2} \Leftrightarrow (x - 2)^{2} + (y + 1)^{2} + 25 = 9 + 16 + 4

    \Leftrightarrow (x - 2)^{2} + \left( \frac{3x}{4} - 4 ight)^{2} = 4 \Leftrightarrow x = \frac{16}{5}

    \Rightarrow y = - \frac{13}{5} \Rightarrow N\left( \frac{16}{5}; - \frac{13}{5};0 ight)

    Vậy x_{N} + y_{N} = \frac{3}{5}

  • Câu 14: Thông hiểu

    Cho hàm số y = f(x) = \frac{2x^{2} + 2x + 5}{2x + 1}. Xét tính đúng sai của các khẳng định sau:

    a) Đạo hàm của hàm số đã cho là f'(x) = \frac{4\left( x^{2} + x + 2 ight)}{(2x + 1)^{2}}. Đúng||Sai

    b) Các điểm cực trị của đồ thị hàm số có toạ độ là (−2; −3) và (1; 3. Đúng||Sai

    c) Đường tiệm cận đứng của đồ thị hàm số có phương trình là: x = - \frac{1}{2}. Đúng||Sai

    d) Đường tiệm cận xiên của đồ thị hàm số có phương trình là y = x + \frac{1}{2}. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) = \frac{2x^{2} + 2x + 5}{2x + 1}. Xét tính đúng sai của các khẳng định sau:

    a) Đạo hàm của hàm số đã cho là f'(x) = \frac{4\left( x^{2} + x + 2 ight)}{(2x + 1)^{2}}. Đúng||Sai

    b) Các điểm cực trị của đồ thị hàm số có toạ độ là (−2; −3) và (1; 3. Đúng||Sai

    c) Đường tiệm cận đứng của đồ thị hàm số có phương trình là: x = - \frac{1}{2}. Đúng||Sai

    d) Đường tiệm cận xiên của đồ thị hàm số có phương trình là y = x + \frac{1}{2}. Đúng||Sai

    a) Ta có:

    f'(x) = \frac{\left( 2x^{2} + 2x + 5 ight)'.(2x + 1) - (2x + 1)'\left( 2x^{2} + 2x + 5 ight)}{(2x + 1)^{2}}

    = \frac{4\left( x^{2} + x - 2 ight)}{(2x + 1)^{2}}

    b) f'(x) = 0 \Leftrightarrow \frac{4\left( x^{2} + x - 2 ight)}{(2x + 1)^{2}} = 0

    \Leftrightarrow x^{2} + x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.

    Thay vào hàm số, ta tính được toạ độ các điểm cực trị là (−2; −3) và (1; 3)

    c) Điều kiện xác định: x eq - \frac{1}{2}

    \lim_{x ightarrow \left( - \frac{1}{2} ight)^{+}}f(x) = + \inftynên x = - \frac{1}{2} là tiệm cận đứng.

    d) y = f(x) = \frac{2x^{2} + 2x + 5}{2x + 1} = x + \frac{1}{2} + \frac{9}{2(2x + 1)}

    Suy ra đồ thị có đường tiệm cận xiên là y = x + \frac{1}{2}.

  • Câu 15: Thông hiểu

    Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích 1800m^{3} và chiều sâu 2m (như hình vẽ).

    Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

    Xét tính đúng sai của các khẳng định sau:

    a) Thể tích bể chứa được tính theo công thức V = 2x^{2}y . Sai|| Đúng

    b) Mối liên hệ giữa x và y là y = \frac{900}{x} . Đúng||Sai

    c) Tổng diện tích mặt bên của bể tính theo x, y là S = 4(x + y) . Đúng||Sai

    d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là 40m . Sai|| Đúng

    Đáp án là:

    Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích 1800m^{3} và chiều sâu 2m (như hình vẽ).

    Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

    Xét tính đúng sai của các khẳng định sau:

    a) Thể tích bể chứa được tính theo công thức V = 2x^{2}y . Sai|| Đúng

    b) Mối liên hệ giữa x và y là y = \frac{900}{x} . Đúng||Sai

    c) Tổng diện tích mặt bên của bể tính theo x, y là S = 4(x + y) . Đúng||Sai

    d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là 40m . Sai|| Đúng

    a) Thể tích của bể là V = B.h = xy.\ h.

    b) Với V = xy.h \Rightarrow 1800 = xy.2 \Rightarrow xy = \frac{1800}{2} = 900.

    c) Tổng diện tích mặt bên gồm 4 hình chữ nhật (trước, sau, trái, phải) là:

    \ S = 2x + 2x + 2y + 2y = 4x + 4y = 4(x + y)

    d) Tổng diện tích của bể là: 4x + 4y + xy = 4x + 4.\frac{900}{x} + 900

    Vì chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể nên chi phí cần có là 4x + 4.\frac{900}{x} + 2.900

    Đặt f(x) = 4x + 4.\frac{900}{x} + 1800 ta có: f'(x) = 4 - \frac{3600}{x^{2}} \Rightarrow f'(x) = 0 \Leftrightarrow x = 30 ta có bảng biến thiên như sau:

    Với x = 30m;y = 30 m và thì chi phí xây dựng bể là thấp nhất.

  • Câu 16: Thông hiểu

    Cho hàm số y = f(x) = x^{2} - 4\ln(1 -x) . Xét tính đúng sai của các khẳng định sau:

    a) Tập xác định của hàm số là D = (1; + \infty) . Sai||Đúng

    b) Đạo hàm của hàm số là y' = \frac{- 2x^{2} + 2x + 4}{1 - x} . Đúng||Sai

    c) Giá trị lớn nhất của hàm số trên \lbrack - 2;0brack là 2. Sai||Đúng

    d) Giá trị nhỏ nhất của hàm số trên \lbrack - 2;0brack là 1 - 4\ln2 . Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) = x^{2} - 4\ln(1 -x) . Xét tính đúng sai của các khẳng định sau:

    a) Tập xác định của hàm số là D = (1; + \infty) . Sai||Đúng

    b) Đạo hàm của hàm số là y' = \frac{- 2x^{2} + 2x + 4}{1 - x} . Đúng||Sai

    c) Giá trị lớn nhất của hàm số trên \lbrack - 2;0brack là 2. Sai||Đúng

    d) Giá trị nhỏ nhất của hàm số trên \lbrack - 2;0brack là 1 - 4\ln2 . Đúng||Sai

    Tập xác định của hàm số là D = (1; + \infty).

    Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

    Ta có: y' = 2x + \frac{4}{1 - x} = \frac{- 2x^{2} + 2x + 4}{1 - x}

    Khi đó y' = 0 \Leftrightarrow \frac{- 2x^{2} + 2x + 4}{1 - x} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1(TM) \\ x = 2(L) \\ \end{matrix} ight.

    Ta có: \left\{ \begin{matrix}f( - 2) = 4 - 4\ln3 \\f( - 1) = 1 - 4\ln2 \\f(0) = 0 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}M = 0 \\m = 1 - 4\ln2 \\\end{matrix} ight.

  • Câu 17: Thông hiểu

    Tìm giá trị của tham số m để hàm số y = \frac{1}{3}x^{3} - (m + 1)x^{2} + \left( m^{2} + 2m ight)x - 3 nghịch biến trên khoảng ( - 1;1)

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Tìm giá trị của tham số m để hàm số y = \frac{1}{3}x^{3} - (m + 1)x^{2} + \left( m^{2} + 2m ight)x - 3 nghịch biến trên khoảng ( - 1;1)

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Thông hiểu

    Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = \frac{1}{2}x - \sqrt{x + 1} trên đoạn \lbrack 0;3brack. Tổng S = 2M - m bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = \frac{1}{2}x - \sqrt{x + 1} trên đoạn \lbrack 0;3brack. Tổng S = 2M - m bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Vận dụng

    Gọi S là tập hợp các giá trị m để tiệm cận xiên của đồ thị hàm số y = \frac{mx^{2} + x - 3}{x - 1} tạo với hai trục hệ tọa độ Oxy một tam giác có diện tích bằng 2. Khi đó tổng các giá trị của S bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Gọi S là tập hợp các giá trị m để tiệm cận xiên của đồ thị hàm số y = \frac{mx^{2} + x - 3}{x - 1} tạo với hai trục hệ tọa độ Oxy một tam giác có diện tích bằng 2. Khi đó tổng các giá trị của S bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Vận dụng cao

    Anh Hùng đang ở trong rừng để đào vàng và tìm thấy vàng ở điểm X cách điểm A một khoảng 3 km. Điểm A nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của anh Hùng nằm ở vị trí Y cách điểm B một khoảng 3 km. Điểm B cũng thuộc đường bờ biển. Biết rằng AB = 3(km),AM = NB = x(km) và AX = BY = 3(km) (minh hoạ như hình vẽ sau).

    Khi đang đào vàng, anh Hùng không may bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo phương trình y = 50\log(t +2). Trong đó, y là nồng độ, t là thời gian tính bằng giờ sau khi bị rắn cắn. Anh cần quay trở lại trại để lấy thuốc giải độc. Anh ấy chạy trong rừng và trên bãi biển với vận tốc lần lượt là 5km/h và 13km/h. Để về đến trại anh Hùng cần chạy từ trong rừng qua điểm M,N trên bãi biển. Tính nồng độ chất độc trong máu thấp nhất khi anh Hùng về đến trại (làm tròn đáp án đến hàng phần chục).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Anh Hùng đang ở trong rừng để đào vàng và tìm thấy vàng ở điểm X cách điểm A một khoảng 3 km. Điểm A nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của anh Hùng nằm ở vị trí Y cách điểm B một khoảng 3 km. Điểm B cũng thuộc đường bờ biển. Biết rằng AB = 3(km),AM = NB = x(km) và AX = BY = 3(km) (minh hoạ như hình vẽ sau).

    Khi đang đào vàng, anh Hùng không may bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo phương trình y = 50\log(t +2). Trong đó, y là nồng độ, t là thời gian tính bằng giờ sau khi bị rắn cắn. Anh cần quay trở lại trại để lấy thuốc giải độc. Anh ấy chạy trong rừng và trên bãi biển với vận tốc lần lượt là 5km/h và 13km/h. Để về đến trại anh Hùng cần chạy từ trong rừng qua điểm M,N trên bãi biển. Tính nồng độ chất độc trong máu thấp nhất khi anh Hùng về đến trại (làm tròn đáp án đến hàng phần chục).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Vận dụng

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Vận dụng

    Cho hàm số y = \frac{mx^{2} + \left( m^{2} + m + 2 ight)x + m^{2} + 3}{x + 1}. Tìm m \in \mathbb{R} để khoảng cách từ gốc O đến tiệm cận xiên hoặc ngang là nhỏ nhất.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \frac{mx^{2} + \left( m^{2} + m + 2 ight)x + m^{2} + 3}{x + 1}. Tìm m \in \mathbb{R} để khoảng cách từ gốc O đến tiệm cận xiên hoặc ngang là nhỏ nhất.

    Chỗ nhập nội dung câu trả lời tự luận
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 4 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập