Lớp 12 Toán 12 - Kết nối tri thức

Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 4

Mô tả thêm: Đề thi giữa HK1 Toán 12 được biên soạn bám sát chương trình sách kết nối tri thức giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức
  • Thời gian làm: 90 phút
  • Số câu hỏi: 22 câu
  • Số điểm tối đa: 22 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Cho hàm số y = - \frac{1}{3}x^{3} + \frac{1}{2}x^{2} + 6x - 1. Khẳng định nào sau đây đúng?

    Tập xác định D\mathbb{= R}

    Ta có: y' = - x^{2} + x + 6 \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 \\ x = 3 \\ \end{matrix} ight.

    Ta có bảng xét dấu

    Suy ra hàm số đồng biến trên khoảng ( - 2,3).

  • Câu 2: Nhận biết

    Cho hàm số y = x^{4} - x^{2} + 6. Xác định số điểm cực trị của hàm số?

    Ta có: y = x^{4} - x^{2} + 6

    Vì a.b = - 1 < 0 nên hàm số đã cho có 3 cực trị.

  • Câu 3: Nhận biết

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng xét dấu của f'(x) như sau:

    Số điểm cực tiểu của hàm số đã cho là

    Đạo hàm f'(x) đổi dấu từ âm sang dương hai lần qua các điểm x = - 2 và x = 2 nên hàm số đã cho có hai điểm cực tiểu.

  • Câu 4: Nhận biết

    Xác định giá trị lớn nhất của hàm số f(x) = x^{3} - 3x + 2 trên đoạn \lbrack - 1;3brack?

    Ta có: f'(x) = 3x^{2} - 3

    \Rightarrow f'(x) = 0 \Leftrightarrow 3x^{2} - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \in \lbrack - 1;3brack \\ x = - 1 \in \lbrack - 1;3brack \\ \end{matrix} ight.

    Ta có: \left\{ \begin{matrix} f( - 1) = 4 \\ f(1) = 0 \\ f(3) = 20 \\ \end{matrix} ight.\ \Rightarrow \underset{\lbrack - 1;3brack}{\max f(x)} = 20 \Leftrightarrow x = 3

    Vậy đáp án cần tìm là 20.

  • Câu 5: Nhận biết

    Tâm đối xứng của đồ thị hàm số y = \frac{3x - 1}{x + 2} là điểm nào sau đây?

    Đồ thị hàm số y = \frac{3x - 1}{x + 2} có tiệm cận đứng x = - 2, tiệm cận ngang y = 3

    Suy ra tâm đối xứng là ( - 2;3).

  • Câu 6: Thông hiểu

    Cho hàm số y = \frac{\sqrt{4 - x}}{\sqrt{x + 1}}. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

    Tập xác định D = ( - 1;4brack suy ra đồ thị hàm số không có đường tiệm cận ngang và đường tiệm cận xiên

    \lim_{x ightarrow ( - 1)^{+}}y = + \infty suy ra đồ thị nhận đường thẳng x = - 1 làm tiệm cận đứng.

    Vậy đồ thị hàm số có một đường tiệm cận.

  • Câu 7: Nhận biết

    Hàm số tương ứng với đồ thị trong hình vẽ dưới đây là:

    Từ đồ thị ta thấy đây là đồ thị hàm số bậc ba có dạng y = ax^{3} + bx^{2} + cx + d với a < 0 nên hàm số tương ứng là y = - x^{3} + 3x.

  • Câu 8: Thông hiểu

    Hàm số nào sau đây có đồ thị như hình vẽ:

    Dựa vào hình dáng đồ thị ta suy ra đồ thị hàm số bậc 4 trùng phương có hệ số a < 0 nên loại đáp án y = x^{4} - 2x^{2} - 1

    Đồ thị hàm số đi qua điểm có tọa độ (0; -1) nên loại đáp án y = - x^{4} +2x^{2}

    Lại có đồ thị hàm số có các điểm cực trị (1;1),( - 1,1) nên loại đáp án y = - x^{4} + 2x^{2} - 1

    Vậy hàm số cần tìm là y = - 2x^{4} +4x^{2} - 1.

  • Câu 9: Thông hiểu

    Cho tứ diện đều ABCD, M là trung điểm cạnh BC. Khi đó \cos(AB;DM) bằng:

    Hình vẽ minh họa

    Giả sử cạnh tứ diện bằng a

    Tam giác BCD đều suy ra DM = \frac{a\sqrt{3}}{2}

    Tam giác ABC đều suy ra AM = \frac{a\sqrt{3}}{2}

    Ta có: \cos\left(\overrightarrow{AB};\overrightarrow{DM} ight) =\frac{\overrightarrow{AB}.\overrightarrow{DM}}{\left|\overrightarrow{AB} ight|.\left| \overrightarrow{DM} ight|} =\frac{\overrightarrow{AB}.\overrightarrow{DM}}{a.\dfrac{a\sqrt{3}}{2}}

    Mặt khác \overrightarrow{AB}.\overrightarrow{DM} = \overrightarrow{AB}.\left( \overrightarrow{AM} - \overrightarrow{AD} ight) = \overrightarrow{AB}.\overrightarrow{AM} - \overrightarrow{AB}.\overrightarrow{AD}

    = \left| \overrightarrow{AB} ight|.\left| \overrightarrow{AM} ight|.cos\left( \overrightarrow{AB};\overrightarrow{AM} ight) - \left| \overrightarrow{AB} ight|.\left| \overrightarrow{AD} ight|.cos\left( \overrightarrow{AB};\overrightarrow{AD} ight)

    = a.\frac{a\sqrt{3}}{2}.\frac{\sqrt{3}}{2} - a.a.\frac{1}{2} = \frac{a^{2}}{4}

    \Rightarrow \cos\left( \overrightarrow{AB};\overrightarrow{DM} ight) = \frac{\sqrt{3}}{6} > 0

    \Rightarrow \left( \overrightarrow{AB};\overrightarrow{DM} ight) = (AB;DM)

    \Rightarrow \cos(AB;DM) = \frac{\sqrt{3}}{6}

  • Câu 10: Thông hiểu

    Hàm số y = f(x) có đạo hàm và liên tục trên \mathbb{R}. Hàm số y = f'(1 - x) có đồ thị như hình vẽ:

    Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?

    Hàm số y = f(x) nghịch biến

    \Leftrightarrow f'(x) < 0 \Leftrightarrow f'(1 - t) < 0 với x = 1 - t

    \Leftrightarrow \left\lbrack \begin{matrix} t < 0 \\ 1 < t < 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} 1 - x < 0 \\ 1 < 1 - x < 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x > 1 \\ - 1 < x < 0 \\ \end{matrix} ight.

    Vậy hàm số y = f(x) nghịch biến trên khoảng ( - 1;0).

  • Câu 11: Thông hiểu

    Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f(x) = \frac{x}{|x| - 1} là:

    Khi x \geq 0;x eq 1 \Rightarrow f(x) = \frac{x}{x - 1}

    Suy ra đồ thị hàm số có 1 tiệm cận ngang y = 1 và 1 tiệm cận đứng x = 1

    Khi x < 0;x eq - 1 \Rightarrow f(x) = \frac{x}{- x - 1}

    Suy ra đồ thị hàm số có 1 tiệm cận ngang y = - 1 và 1 tiệm cận đứng x = - 1

    Vậy đồ thị hàm số y = f(x) = \frac{x}{|x| - 1} có tất cả 4 đường tiệm cận.

  • Câu 12: Thông hiểu

    Hình vẽ nào sau đây là đồ thị của hàm số y = (x - c)(d - x)^{2} với c > d > 0?

    Với c > d > 0 thì đồ thị hàm số y = (x - c)(d - x)^{2} theo thứ tự tiếp xúc với trục hoành tại điểm có hoành độ x = d và x = c

    Mặt khác với x \leq c thì y \leq 0 nên khi x \leq c thì đồ thị hàm số nằm phía dưới trục hoành

    Vậy đồ thị hàm số cần tìm là .

  • Câu 13: Nhận biết

    Cho hàm số y = f(x) xác định trên \mathbb{R}\left\{ \pm 2 ight\} và có bảng biến thiên như sau:

    Xét tính đúng sai của các khẳng định sau.

    a) Hàm số không có điểm cực trị. Đúng||Sai

    b) \lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty. Sai||Đúng

    c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

    d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x) xác định trên \mathbb{R}\left\{ \pm 2 ight\} và có bảng biến thiên như sau:

    Xét tính đúng sai của các khẳng định sau.

    a) Hàm số không có điểm cực trị. Đúng||Sai

    b) \lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty. Sai||Đúng

    c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

    d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

    Dựa vào bảng biến thiên ta thấy

    a) Hàm số không có điểm cực trị.

    b) lim \lim_{x ightarrow ( - 2)^{-}}f(x) = - 10.

    c) \lim_{x ightarrow \pm \infty}f(x) = 0. Suy ra đồ thị có đúng 1 đường tiệm cận ngang là y = 0.

    d) \lim_{x ightarrow ( - 2)^{+}}f(x) = + \infty và \lim_{x ightarrow 2^{+}}f(x) = + \infty nên đồ thị hàm số có đúng 2 đường tiệm cận đứng x = \pm 2.

  • Câu 14: Thông hiểu

    Trong không gian Oxyz, cho ba điểm A( - 1; - 2;3),B(0;3;1),C(4;2;2). Các khẳng định sau là đúng hay sai?

    a) \overrightarrow{AB}.\overrightarrow{AC} = - 27. Sai||Đúng

    b) \cos(\overrightarrow{AB},\overrightarrow{AC}) =\frac{9}{2\sqrt{35}}. Sai||Đúng

    c) \overrightarrow{AC}.\overrightarrow{CB} = 15. Đúng||Sai

    d) \cos(\overrightarrow{AB},\overrightarrow{BC}) =\frac{5}{2\sqrt{21}}. Đúng||Sai

    Đáp án là:

    Trong không gian Oxyz, cho ba điểm A( - 1; - 2;3),B(0;3;1),C(4;2;2). Các khẳng định sau là đúng hay sai?

    a) \overrightarrow{AB}.\overrightarrow{AC} = - 27. Sai||Đúng

    b) \cos(\overrightarrow{AB},\overrightarrow{AC}) =\frac{9}{2\sqrt{35}}. Sai||Đúng

    c) \overrightarrow{AC}.\overrightarrow{CB} = 15. Đúng||Sai

    d) \cos(\overrightarrow{AB},\overrightarrow{BC}) =\frac{5}{2\sqrt{21}}. Đúng||Sai

    Ta có \overrightarrow{AB} = (1;5; - 2),\overrightarrow{AC} = (5;4; - 1),\overrightarrow{AC} = (4; - 1;1).

    Ta có:

    \overrightarrow{AB}.\overrightarrow{AC} = 5 + 20 + 2 = 27.

    Ta có:

    \overrightarrow{AC}.\overrightarrow{CB} = 5.( - 4) + 4.1 + ( - 1).( - 1) = - 15.

    Ta có:

    \cos(\overrightarrow{AB},\overrightarrow{AC}) =\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB} ight|.|\overrightarrow{AC}|} =\frac{27}{\sqrt{30}.\sqrt{42}} = \frac{9}{2\sqrt{35}}.

    Ta có:

    \cos(\overrightarrow{AB},\overrightarrow{BC}) =\frac{\overrightarrow{AB}.\overrightarrow{BC}}{\left|\overrightarrow{AB} ight||\overrightarrow{BC}|} =\frac{15}{\sqrt{42}.\sqrt{18}} = \frac{5}{2\sqrt{21}}.

  • Câu 15: Vận dụng

    Một bể bơi chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng đồ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.

    a) Sau t phút khối lượng muối trong bể là 750t (gam). Đúng||Sai

    b) Nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là f(t) = \frac{30t}{200 - t} . Sai||Đúng

    c) Xem y = f(t) là một hàm số xác định trên nửa khoảng \lbrack 0; + \infty) , tiệm cận ngang của đồ thị hàm số đó có phương trình là y = 30 . Đúng||Sai

    d) Khi t ngày càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Đúng||Sai

    Đáp án là:

    Một bể bơi chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng đồ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.

    a) Sau t phút khối lượng muối trong bể là 750t (gam). Đúng||Sai

    b) Nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là f(t) = \frac{30t}{200 - t} . Sai||Đúng

    c) Xem y = f(t) là một hàm số xác định trên nửa khoảng \lbrack 0; + \infty) , tiệm cận ngang của đồ thị hàm số đó có phương trình là y = 30 . Đúng||Sai

    d) Khi t ngày càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Đúng||Sai

    Sau t phút, khối lượng muối trong bể là 25.30.t = 750t (gam)

    Thể tích của lượng nước trong bể là 5000 + 25t (lít).

    Vậy nồng độ muối sau t phút là: f(t) = \frac{750t}{5000 + 25t} = \frac{30t}{200 + t} (gam/lít).

    Ta có \lim_{t ightarrow + \infty}f(t) = \lim_{t ightarrow + \infty}\frac{30t}{200 + t} = \lim_{x ightarrow + \infty}\left( 30 - \frac{6000}{200 + t} ight) = 30

    Vậy đường thẳng y = 30 là tiệm cận ngang của đồ thị hàm số f(t):

    Ta có đồ thị hàm số y = f(t) nhận đường thẳng y = 30 làm đường tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít).

    Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ nước muối bơm vào bể.

    a) Đúng. b) Sai. c) Đúng. d) Đúng.

  • Câu 16: Thông hiểu

    Cho hàm số y = f(x)xác định trên R và có đồ thị hàm số y = f'(x) là đường cong như hình vẽ:

    Hãy cho biết tính đúng sai của mỗi mệnh đề dưới đây.

    a) Hàm số y = f(x) nghịch biến trên khoảng (−1; 1). Sai||Đúng

    b) Hàm số y = f(x) nghịch biến trên khoảng (0; 2). Đúng||Sai

    c) Hàm số y = f(x) đạt cực đại tại x = 0. Đúng||Sai

    d) Hàm số y = f(x) đạt cực tiểu tại x = 1. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x)xác định trên R và có đồ thị hàm số y = f'(x) là đường cong như hình vẽ:

    Hãy cho biết tính đúng sai của mỗi mệnh đề dưới đây.

    a) Hàm số y = f(x) nghịch biến trên khoảng (−1; 1). Sai||Đúng

    b) Hàm số y = f(x) nghịch biến trên khoảng (0; 2). Đúng||Sai

    c) Hàm số y = f(x) đạt cực đại tại x = 0. Đúng||Sai

    d) Hàm số y = f(x) đạt cực tiểu tại x = 1. Sai||Đúng

    Từ đồ thị hàm số y = f'(x), ta có bảng biến thiên

    a) Từ bảng biến thiên hàm số đồng biến trên khoảng (−1; 0) và nghịch biến trên khoảng (0; 1).

    b) Từ bảng biến thiên ta thấy hàm số y = f(x) nghịch biến trên (0; 2).

    c) Từ bảng biến thiên ta thấy hàm số f(x) đạt cực đại tại x = 0.

    d) Từ bảng biến thiên ta thấy hàm số f(x) đạt cực tiểu tại x = −2 và x = 2.

  • Câu 17: Thông hiểu

    Cho hàm số y =f(x) = - \frac{1}{3}x^{3} + ax^{2} + (3a + 2)x - 5. Tập hợp các giá trị của tham số a để hàm số y = f(x) nghịch biến trên \mathbb{R} là \lbrack m;nbrack. Tính giá trị biểu thức T=2m-n?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y =f(x) = - \frac{1}{3}x^{3} + ax^{2} + (3a + 2)x - 5. Tập hợp các giá trị của tham số a để hàm số y = f(x) nghịch biến trên \mathbb{R} là \lbrack m;nbrack. Tính giá trị biểu thức T=2m-n?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Thông hiểu

    Cho hàm số y = f(x) = \frac{2x^{2} + 26x + 18}{x + 13} có điểm cực tiểu và điểm cực đại lần lượt là x_{1};x_{2}. Tính P = - 2x_{1} + x_{2}?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = \frac{2x^{2} + 26x + 18}{x + 13} có điểm cực tiểu và điểm cực đại lần lượt là x_{1};x_{2}. Tính P = - 2x_{1} + x_{2}?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Thông hiểu

    Cho hàm số y = f(x) = ax^{3} + bx^{2} +cx + d;(a eq 0) có đồ thị như sau:

    Hàm số y = \left| f(x) ight| có bao nhiêu điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = ax^{3} + bx^{2} +cx + d;(a eq 0) có đồ thị như sau:

    Hàm số y = \left| f(x) ight| có bao nhiêu điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Vận dụng

    Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m^{2}. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn đồng/m2. Hãy xác định chi phí thấp nhất để xây bể.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m^{2}. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn đồng/m2. Hãy xác định chi phí thấp nhất để xây bể.

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Vận dụng

    Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = \frac{\sqrt{1 - x}}{x^{2} + 4x + m} có đúng ba đường tiệm cận?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = \frac{\sqrt{1 - x}}{x^{2} + 4x + m} có đúng ba đường tiệm cận?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Vận dụng cao

    Cho hàm số f(x) mà đồ thị hàm số y = f’(x) được biểu diễn như hình vẽ:

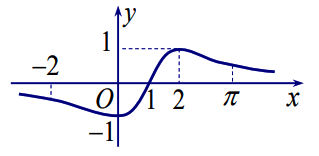
    Bất phương trình nghiệm đúng với mọi x thuộc khoảng

    Giả sử bất phương trình f\left( x ight) > \sin \frac{{\pi x}}{2} + m nghiệm đúng với mọi x \in \left[ { - 1;3} ight] thì tham số m thỏa mãn điều kiện là:

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số f(x) mà đồ thị hàm số y = f’(x) được biểu diễn như hình vẽ:

    Bất phương trình nghiệm đúng với mọi x thuộc khoảng

    Giả sử bất phương trình f\left( x ight) > \sin \frac{{\pi x}}{2} + m nghiệm đúng với mọi x \in \left[ { - 1;3} ight] thì tham số m thỏa mãn điều kiện là:

    Chỗ nhập nội dung câu trả lời tự luận
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 4 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 3 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi giữa kì 1 Toán 12 Kết nối tri thức Đề 4
Thời gian còn lại 90:00 Số câu đã làm 0/22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập