Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng sau:
Do nên hàm số
nghịch biến trên khoảng
.
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng sau:
Do nên hàm số
nghịch biến trên khoảng
.
Cho hàm số ![]() có đồ thị như hình vẽ:
có đồ thị như hình vẽ:

Giá trị cực tiểu của hàm số đã cho bằng:
Dựa vào đồ thị của hàm số ta thấy giá trị cực tiểu của hàm số bằng -2.
Biết rằng hàm số ![]() đạt giá trị nhỏ nhất trên
đạt giá trị nhỏ nhất trên ![]() tại điểm
tại điểm ![]() . Khi đó giá trị biểu thức
. Khi đó giá trị biểu thức ![]() bằng:
bằng:
Ta có:
Mà khi
Suy ra .
Đồ thị hàm số ![]() có bao nhiêu đường tiệm cận?
có bao nhiêu đường tiệm cận?
Ta có:
suy ra
là tiệm cận đứng của đồ thị hàm số.
suy ra đồ thị hàm số có tiệm cận ngang là
.
Vậy đồ thị hàm số có hai đường tiệm cận.
Cho hàm số bậc ba ![]() có đồ thị như sau:
có đồ thị như sau:

Số giá trị nguyên của tham số ![]() để phương trình
để phương trình ![]() có ba nghiệm phân biệt là:
có ba nghiệm phân biệt là:
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
và đường thẳng
Suy ra để phương trình có ba nghiệm phân biệt thì
Vì
Vậy có duy nhất một số nguyên của thỏa mãn yêu cầu bài toán.
Cho tứ diện ![]() có
có ![]() và
và ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() . Hãy xác định góc giữa các cặp vectơ
. Hãy xác định góc giữa các cặp vectơ ![]() và
và ![]() ?
?
Hình vẽ minh họa
Xét tam giác ICD có I là trung điểm đoạn CD
Tam giác ABC có và
suy ra tam giác
đều suy ra
Tương tự ta cũng có tam giác ABD đều nên
Ta có:
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Vectơ
. Vectơ ![]() có tọa độ là:
có tọa độ là:
Ta có:
Vậy đáp án đúng là: .
Trong không gian hệ trục tọa độ ![]() , cho các điểm
, cho các điểm ![]() . Biết rằng tứ giác
. Biết rằng tứ giác ![]() là hình bình hành, khi đó tọa độ điểm
là hình bình hành, khi đó tọa độ điểm ![]() là:
là:
Giả sử điểm ta có
là hình bình hành nên
. Vậy tọa độ điểm
.
Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Tính
. Tính ![]() ?
?
Ta có:
Người ta thống kê tốc độ của một số xe ôtô di chuyển qua một trạm kiểm soát trên đường cao tốc trong một khoảng thời gian ở bảng sau:
|
Tốc độ (km/h) |
[75; 80) |
[80; 85) |
[85; 90) |
[90; 95) |
[95; 100) |
|
Số xe |
15 |
22 |
28 |
34 |
19 |
Khoảng biến thiên của mẫu số liệu ghép nhóm đã cho là:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 100 - 75 = 25 km/h.
Kết quả thống kê điểm trung bình năm học của hai lớp 12C và 12D như sau:
|
Điểm trung bình |
[5; 6) |
[6; 7) |
[7; 8) |
[8; 9) |
[9; 10) |
|
Số học sinh lớp 12C |
4 |
5 |
3 |
4 |
2 |
|
Số học sinh lớp 12CD |
2 |
5 |
4 |
3 |
1 |
Điểm trung bình của lớp 12C và điểm trung bình của lớp 12D lần lượt là:
Ta có:
|
Điểm trung bình |
[5; 6) |
[6; 7) |
[7; 8) |
[8; 9) |
[9; 10) |
|
Giá trị đại diện |
5,5 |
6,5 |
7,5 |
8,5 |
9,5 |
|
Số học sinh lớp 12C |
4 |
5 |
3 |
4 |
2 |
|
Số học sinh lớp 12CD |
2 |
5 |
4 |
3 |
1 |
Điểm trung bình của lớp 12C:
.
Điểm trung bình của lớp 12D:
.
Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có:
Vậy khẳng định đúng là
Cho hàm số ![]() xác định trên tập số thực và có đạo hàm
xác định trên tập số thực và có đạo hàm ![]() . Xét tính đúng sai của các khẳng định sau:
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
b) Hàm số nghịch biến trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
c) Đồ thị hàm số có hai điểm cực trị. Sai|| Đúng
d) Đồ thị hàm số có một điểm cực tiểu. Đúng||Sai
Cho hàm số xác định trên tập số thực và có đạo hàm
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng . Đúng||Sai
b) Hàm số nghịch biến trên khoảng . Đúng||Sai
c) Đồ thị hàm số có hai điểm cực trị. Sai|| Đúng
d) Đồ thị hàm số có một điểm cực tiểu. Đúng||Sai
Ta có:
Bảng biến thiên:
a) Hàm số đồng biến trên khoảng .
b) Hàm số nghịch biến trên khoảng nên nghịch biến trên
.
c) Hàm số có đúng một điểm cực trị.
d) Hàm số có đúng một điểm cực tiểu .
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức ![]() trong đó
trong đó ![]() là liều lượng thuốc được tiêm cho bệnh nhân (
là liều lượng thuốc được tiêm cho bệnh nhân (![]() được tính bằng miligam,
được tính bằng miligam, ![]() ).
).
a) Độ giảm huyết áp của một bệnh nhân là ![]() . Đúng||Sai
. Đúng||Sai
b) Đạo hàm của ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
c) Phương trình ![]() có nghiệm duy nhất. Sai||Đúng
có nghiệm duy nhất. Sai||Đúng
d) Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là ![]() . Đúng||Sai
. Đúng||Sai
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức trong đó
là liều lượng thuốc được tiêm cho bệnh nhân (
được tính bằng miligam,
).
a) Độ giảm huyết áp của một bệnh nhân là . Đúng||Sai
b) Đạo hàm của là
. Sai||Đúng
c) Phương trình có nghiệm duy nhất. Sai||Đúng
d) Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là . Đúng||Sai
a) Đúng. Độ giảm huyết áp của một bệnh nhân được viết lại là.
b) Sai. Đạo hàm của là
.
c) Sai. Xét phương trình
d) Đúng. Ta có bảng biến thiên:
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là 20 mg.
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Các khẳng định sau là đúng hay sai?
. Các khẳng định sau là đúng hay sai?
a) Tọa độ điểm A là ![]() . Đúng||Sai
. Đúng||Sai
b) Hình chiếu vuông góc của ![]() lên trục
lên trục ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
c) Trung điểm của ![]() là
là ![]() . Đúng||Sai
. Đúng||Sai
d) Hình chiếu vuông góc của ![]() lên mặt phẳng
lên mặt phẳng ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
Trong không gian , cho vectơ
. Các khẳng định sau là đúng hay sai?
a) Tọa độ điểm A là . Đúng||Sai
b) Hình chiếu vuông góc của lên trục
là
. Sai||Đúng
c) Trung điểm của là
. Đúng||Sai
d) Hình chiếu vuông góc của lên mặt phẳng
là
. Sai||Đúng
a) Ta có
b) Hình chiếu vuông góc của A lên Ox là .
c) Trung điểm của là điểm
.
d) Hình chiếu vuông góc của lên mặt phẳng
là
.
Thống kê thu nhập theo tháng của một số nhân viên trong phòng A (đơn vị: triệu đồng) được cho trong bảng sau:
|
Thu nhập |
[3; 5) |
[5; 7) |
[7; 9) |
[9; 11) |
|
Số nhân viên |
5 |
10 |
5 |
2 |
Xét tính đúng, sai các mệnh đề sau:
(a) Cỡ mẫu là n = 22. Đúng||Sai
(b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là ![]() . Sai|| Đúng
. Sai|| Đúng
(c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là ![]() . Sai|| Đúng
. Sai|| Đúng
(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: ![]() . Sai|| Đúng
. Sai|| Đúng
Thống kê thu nhập theo tháng của một số nhân viên trong phòng A (đơn vị: triệu đồng) được cho trong bảng sau:
|
Thu nhập |
[3; 5) |
[5; 7) |
[7; 9) |
[9; 11) |
|
Số nhân viên |
5 |
10 |
5 |
2 |
Xét tính đúng, sai các mệnh đề sau:
(a) Cỡ mẫu là n = 22. Đúng||Sai
(b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là . Sai|| Đúng
(c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là . Sai|| Đúng
(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: . Sai|| Đúng
Ta có:
|
Thu nhập |
[3; 5) |
[5; 7) |
[7; 9) |
[9; 11) |
|
Số nhân viên |
5 |
10 |
5 |
2 |
|
Tần số tích lũy |
5 |
15 |
20 |
22 |
(a) Cỡ mẫu là n = 22
Chọn ĐÚNG.
(b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là .
Ta có:
Ta có:
=> Nhóm chứa là [5; 7)
Khi đó ta tìm được các giá trị:
Chọn SAI
(c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là .
Ta có:
=> Nhóm chứa là [7; 9)
Khi đó ta tìm được các giá trị:
.
Chọn SAI
(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: .
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
Chọn SAI
Cho hàm số ![]() với
với ![]() là tham số. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
là tham số. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số ![]() để hàm số đã cho đồng biến trên
để hàm số đã cho đồng biến trên ![]() ?
?
Cho hàm số với
là tham số. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
để hàm số đã cho đồng biến trên
?
Bác T làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp có chiều dài gấp đôi chiều rộng. Biết rằng bác T sử dụng hết ![]() kính. Hỏi dung tích lớn nhất của bế cá bằng bao nhiêu?
kính. Hỏi dung tích lớn nhất của bế cá bằng bao nhiêu?
Bác T làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp có chiều dài gấp đôi chiều rộng. Biết rằng bác T sử dụng hết kính. Hỏi dung tích lớn nhất của bế cá bằng bao nhiêu?
Xác định các giá trị của tham số ![]() để hàm số
để hàm số ![]() có ba điểm cực trị sao cho giá trị cực đại của hàm số đạt giá trị nhỏ nhất?
có ba điểm cực trị sao cho giá trị cực đại của hàm số đạt giá trị nhỏ nhất?
Xác định các giá trị của tham số để hàm số
có ba điểm cực trị sao cho giá trị cực đại của hàm số đạt giá trị nhỏ nhất?
Cho hình lập phương ![]() có đường chéo
có đường chéo ![]() . Gọi
. Gọi ![]() là tâm hình vuông
là tâm hình vuông ![]() và điểm S thỏa mãn:
và điểm S thỏa mãn: ![]()
![]() . Khi đó độ dài của đoạn
. Khi đó độ dài của đoạn ![]() bằng
bằng ![]() với
với ![]() và
và ![]() là phân số tối giản. Tính giá trị của biểu thức
là phân số tối giản. Tính giá trị của biểu thức ![]() .
.
Cho hình lập phương có đường chéo
. Gọi
là tâm hình vuông
và điểm S thỏa mãn:
. Khi đó độ dài của đoạn
bằng
với
và
là phân số tối giản. Tính giá trị của biểu thức
.
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình:
Độ tuổi | [50; 55) | [55; 60) | [60; 65) | [65; 70) | [70; 75) | [75; 80) | [80; 85) | [85; 90) |
Nam | 4 | 7 | 4 | 6 | 15 | 12 | 2 | 0 |
Nữ | 3 | 4 | 5 | 3 | 7 | 14 | 13 | 1 |
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm có tuổi thọ trung bình đồng đều nhất?
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình:
Độ tuổi | [50; 55) | [55; 60) | [60; 65) | [65; 70) | [70; 75) | [75; 80) | [80; 85) | [85; 90) |
Nam | 4 | 7 | 4 | 6 | 15 | 12 | 2 | 0 |
Nữ | 3 | 4 | 5 | 3 | 7 | 14 | 13 | 1 |
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm có tuổi thọ trung bình đồng đều nhất?
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau:
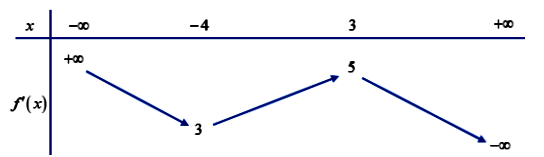
Bất phương trình ![]() có nghiêm đúng với
có nghiêm đúng với ![]() khi và chỉ khi :
khi và chỉ khi :
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau:

Bất phương trình có nghiêm đúng với
khi và chỉ khi :
