Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng cho dưới đây?
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng .
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng cho dưới đây?
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng .
Đồ thị hàm số ![]() được biểu diễn bởi hình vẽ:
được biểu diễn bởi hình vẽ:

Điểm cực tiểu của hàm số đã cho là:
Quan sát đồ thị của hàm số ta thấy hàm số có điểm cực tiểu là .
Giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng:
bằng:
Tập xác định nên hàm số xác định và liên tục trên
Ta có:
Mà
Cho hàm số ![]() . Khi đó tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
. Khi đó tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Ta có:
suy ra đồ thị hàm số có tiệm cận đứng là
suy ra đồ thị hàm số có tiệm cận ngang là
Vậy đồ thị hàm số có tổng số đường tiệm cận đứng và đườn tiệm cận ngang bằng 2.
Hàm số ![]() có đồ thị như sau:
có đồ thị như sau:

Tìm điều kiện của tham số ![]() để phương trình
để phương trình ![]() có
có ![]() nghiệm dương?
nghiệm dương?
Để số nghiệm dương của phương trình đã cho bằng 1 thì đường thẳng cắt đồ thị hàm số
tại một điểm có hoành độ dương
.
Cho tứ diện ![]() có
có ![]() và
và ![]() . Hãy xác định góc giữa cặp vectơ
. Hãy xác định góc giữa cặp vectơ ![]() và
và ![]() ?
?
Hình vẽ minh họa
Ta có:
Mà
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() đi qua điểm nào sau đây?
đi qua điểm nào sau đây?
Xét điểm ta có:
đúng nên
.
Tứ giác ![]() là hình bình hành biết tọa độ các điểm
là hình bình hành biết tọa độ các điểm ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() ?
?
Giả sử điểm khi đó
ta có là hình bình hành nên
. Vậy tọa độ điểm
.
Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Tính
. Tính ![]() ?
?
Ta có:
Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:
|
Lượng nước (m3) |
[3; 6) |
[6; 9) |
[9; 12) |
[12; 15) |
[15; 18) |
|
Số hộ gia đình |
20 |
60 |
40 |
32 |
7 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số loại máy tính xách tay được mô tả như sau:

Tính thời gian sử dụng pin trung bình?
Ta có:
|
Thời gian (giờ) |
[7,2; 7,4) |
[7,4; 7,6) |
[7,6; 7,8) |
[7,8; 8,0) |
|
Giá trị đại diện |
7,3 |
7,5 |
7,7 |
7,9 |
|
Số máy vi tính |
2 |
4 |
7 |
5 |
Thòi gian trung bình là:
giờ
Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có: suy ra “
” là khẳng định sai.
Cho hàm số ![]() . Xét tính đúng sai của các khẳng định sau:
. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho đạt cực đại tại ![]() . Đúng||Sai
. Đúng||Sai
b) Hàm số đã cho đạt cực tiểu tại ![]() . Sai|| Đúng
. Sai|| Đúng
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là ![]() . Sai|| Đúng
. Sai|| Đúng
d) Đồ thị hàm số ![]() có điểm cực đại là
có điểm cực đại là ![]() . Sai|| Đúng
. Sai|| Đúng
Cho hàm số . Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho đạt cực đại tại . Đúng||Sai
b) Hàm số đã cho đạt cực tiểu tại . Sai|| Đúng
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là . Sai|| Đúng
d) Đồ thị hàm số có điểm cực đại là
. Sai|| Đúng
Ta có:
Bảng biến thiên
a) Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
b) Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại
c) Dựa vào bảng biến thiên ta thấy hàm số giá trị cực đại và cực tiểu lần lượt là
d) Dựa vào bảng biến thiên ta thấy hàm số có được bằng cách tịnh tiến đồ thị
lên trên 3 đơn vị. Suy ra đồ thị hàm số
có điểm cực đại là
.
Cho hàm số ![]() xác định trên tập
xác định trên tập ![]() và một số thực
và một số thực ![]() . Xét tính đúng sai của các khẳng định sau:
. Xét tính đúng sai của các khẳng định sau:
a) Nếu ![]() thì
thì ![]() . Sai|| Đúng
. Sai|| Đúng
b) Nếu ![]() thì
thì ![]() . Sai|| Đúng
. Sai|| Đúng
c) Nếu ![]() thì
thì ![]() . Đúng||Sai
. Đúng||Sai
d) Nếu ![]() thì
thì ![]() . Đúng||Sai
. Đúng||Sai
Cho hàm số xác định trên tập
và một số thực
. Xét tính đúng sai của các khẳng định sau:
a) Nếu thì
. Sai|| Đúng
b) Nếu thì
. Sai|| Đúng
c) Nếu thì
. Đúng||Sai
d) Nếu thì
. Đúng||Sai
a) Khẳng định này sai, cần bổ sung thêm điều kiện để
.
b) Khẳng định này sai, cần bổ sung thêm điều kiện để
.
c) Nếu thì
là hàm hằng trên
(đồ thị là đường thẳng nằm ngang).
Suy ra .
d) Nếu thì
là hàm hằng trên
(đồ thị là đường thẳng nằm ngang).
Suy ra.
Cho hình chóp ![]() có đáy
có đáy ![]() là hình chữ nhật. Biết rằng cạnh
là hình chữ nhật. Biết rằng cạnh ![]() , cạnh bên
, cạnh bên ![]() và vuông góc với mặt đáy. Gọi
và vuông góc với mặt đáy. Gọi ![]() lần lượt là trung điểm của các cạnh SB, SD. Xét tính đúng sai của các khẳng định sau:
lần lượt là trung điểm của các cạnh SB, SD. Xét tính đúng sai của các khẳng định sau:
a) Hai vectơ ![]() là hai vectơ cùng phương, cùng hướng. Sai||Đúng
là hai vectơ cùng phương, cùng hướng. Sai||Đúng
b) Góc giữa hai vectơ ![]() bằng
bằng ![]() . Sai||Đúng
. Sai||Đúng
c) Tích vô hướng của ![]() bằng
bằng ![]() . Đúng||Sai
. Đúng||Sai
d) Độ dài vectơ ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
Cho hình chóp có đáy
là hình chữ nhật. Biết rằng cạnh
, cạnh bên
và vuông góc với mặt đáy. Gọi
lần lượt là trung điểm của các cạnh SB, SD. Xét tính đúng sai của các khẳng định sau:
a) Hai vectơ là hai vectơ cùng phương, cùng hướng. Sai||Đúng
b) Góc giữa hai vectơ bằng
. Sai||Đúng
c) Tích vô hướng của bằng
. Đúng||Sai
d) Độ dài vectơ là
. Sai||Đúng
a) Sai
Ta thấy ABCD là hình chữ nhật nên
Suy ra hai vectơ là hai vectơ cùng phương, ngược hướng.
b) Sai
Ta có ABCD là hình chữ nhật nên
Hình chóp S.ABCD có SA vuông góc với mặt đáy nên tam giác SAC là tam giác vuông tại A.
Suy ra
Ta có:
c) Đúng
Hình chóp S. ABCD có SA vuông góc với mặt đáy nên tam giác SAB là tam giác vuông tại A.
Suy ra
Trong tam giác SAB vuông tại A có AM là đường trung tuyến nên:
Lại có M là trung điểm của SB nên
Ta tính được
Mà
d) Sai
Ta có: M, N lần lượt là trung điểm của các cạnh SB, SD nên MN là đường trung bình của tam giác SBD
Do đó
Suy ra
Cho mẫu số liệu ghép nhóm dưới đây:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
|
Tần số |
2 |
6 |
8 |
9 |
3 |
2 |
Xét tính đúng sai của các khẳng định sau?
a) Khoảng biến thiên của mẫu số liệu R = 5. Đúng||Sai
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm bằng ![]() . Sai||Đúng
. Sai||Đúng
c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm bằng ![]() . Sai||Đúng
. Sai||Đúng
d) Khoảng tứ phân vị của mẫu số liệu ![]() . Đúng||Sai
. Đúng||Sai
Cho mẫu số liệu ghép nhóm dưới đây:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
|
Tần số |
2 |
6 |
8 |
9 |
3 |
2 |
Xét tính đúng sai của các khẳng định sau?
a) Khoảng biến thiên của mẫu số liệu R = 5. Đúng||Sai
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm bằng . Sai||Đúng
c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm bằng . Sai||Đúng
d) Khoảng tứ phân vị của mẫu số liệu . Đúng||Sai
a) Đúng: Từ mẫu số liệu bảng trên ta có khoảng biến thiên của mẫu số liệu R = 5
Ta có:
⇒ Suy ra nhóm chứa tứ phân vị thứ nhất là nhóm [55; 56).
b) Sai: Áp dụng công thức:
c) Sai: Ta có suy ra nhóm chứa tứ phân vị thứ ba là nhóm [57;58).
d) Đúng: Suy ra khoảng tứ phân vị của mẫu số liệu trên là .
Xác định tổng ![]() tất cả các giá trị nguyên của tham số
tất cả các giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() nghịch biến trên từng khoảng xác định?
nghịch biến trên từng khoảng xác định?
Xác định tổng tất cả các giá trị nguyên của tham số
để hàm số
nghịch biến trên từng khoảng xác định?
Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật ![]() , trong đó
, trong đó ![]() là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi
là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi ![]() bằng bao nhiêu?
bằng bao nhiêu?
Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật , trong đó
là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi
bằng bao nhiêu?
Một tạp chí bán được 25 000 đồng một cuốn. Chi phía xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, …) được cho bởi công thức ![]() , C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 6 000 đồng. Các khoản thu khi bán tạp chí bao gồm tiền bán tạp chí và 100 triệu đồng nhận được từ quảng cá. Giả sử số cuốn in ra đều được bán hết. Tính số tiền lãi lớn nhất có thể có khi bán tạp chí.
, C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 6 000 đồng. Các khoản thu khi bán tạp chí bao gồm tiền bán tạp chí và 100 triệu đồng nhận được từ quảng cá. Giả sử số cuốn in ra đều được bán hết. Tính số tiền lãi lớn nhất có thể có khi bán tạp chí.
Một tạp chí bán được 25 000 đồng một cuốn. Chi phía xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, …) được cho bởi công thức , C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 6 000 đồng. Các khoản thu khi bán tạp chí bao gồm tiền bán tạp chí và 100 triệu đồng nhận được từ quảng cá. Giả sử số cuốn in ra đều được bán hết. Tính số tiền lãi lớn nhất có thể có khi bán tạp chí.
Để đồ thị hàm số ![]() có ba điểm cực trị tạo thành một tam giác có diện tích bằng
có ba điểm cực trị tạo thành một tam giác có diện tích bằng ![]() . Tìm giá trị tham số
. Tìm giá trị tham số ![]() thỏa mãn yêu cầu bài toán?
thỏa mãn yêu cầu bài toán?
Để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có diện tích bằng
. Tìm giá trị tham số
thỏa mãn yêu cầu bài toán?
Cho tứ diện ![]() và các điểm
và các điểm ![]() xác định bởi
xác định bởi ![]() . Tìm giá trị
. Tìm giá trị ![]() để
để ![]() đồng phẳng?
đồng phẳng?
Cho tứ diện và các điểm
xác định bởi
. Tìm giá trị
để
đồng phẳng?
Cho bảng thống kê số lượt vi phạm giao thông trong 20 ngày của người dân một địa phương được thống kê như sau:
101 | 79 | 79 | 78 | 75 |
73 | 68 | 67 | 67 | 63 |
63 | 61 | 60 | 59 | 57 |
55 | 55 | 50 | 47 | 42 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm có độ dài bằng nhau với nhóm đầu tiên là [40; 50)?
Cho bảng thống kê số lượt vi phạm giao thông trong 20 ngày của người dân một địa phương được thống kê như sau:
101 | 79 | 79 | 78 | 75 |
73 | 68 | 67 | 67 | 63 |
63 | 61 | 60 | 59 | 57 |
55 | 55 | 50 | 47 | 42 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm có độ dài bằng nhau với nhóm đầu tiên là [40; 50)?
Cho hàm số ![]() có đồ thị của đạo hàm f’(x) như hình vẽ:
có đồ thị của đạo hàm f’(x) như hình vẽ:
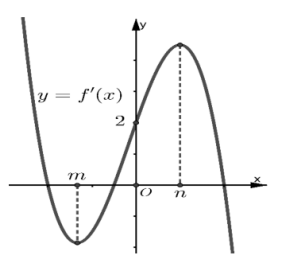
Biết rằng e > n. Số điểm cực trị của hàm số ![]() bằng bao nhiêu?
bằng bao nhiêu?
Cho hàm số có đồ thị của đạo hàm f’(x) như hình vẽ:

Biết rằng e > n. Số điểm cực trị của hàm số bằng bao nhiêu?
