Lớp 12 Toán 12 - Kết nối tri thức

Đề thi HK1 Toán 12 Kết nối tri thức Đề 1

Mô tả thêm: Đề thi HK1 Toán 12 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức toán 12 kết nối tri thức.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 22 câu
  • Số điểm tối đa: 22 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Cho hàm số y = f(x) có đạo hàm trên \mathbb{R} là f'(x) = x^{2}(x - 1). Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

    Ta có: f'(x) = 0 \Leftrightarrow x^{2}(x - 1) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.. Lập bảng xét dấu như sau:

    Suy ra hàm số y = f(x) đồng biến trên khoảng (1; + \infty)

  • Câu 2: Nhận biết

    Cho hàm số f(x) xác định và liên tục trên \mathbb{R} có bảng xét dấu như sau:

    Số điểm cực trị của hàm số đã cho là:

    Dựa vào bảng xét dấu của f'(x) ta thấy f'(x) đổi dấu 4 lần và hàm số y = f(x) xác định và liên tục trên \mathbb{R}

    Suy ra hàm số có 4 điểm cực trị.

  • Câu 3: Thông hiểu

    Cho hàm số y = \frac{x - m^{2}}{x + 2} với m là tham số. Tích tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số đã cho trên đoạn \lbrack - 1;1brack bằng \frac{1}{4} bằng:

    Ta có: y' = \frac{2 + m^{2}}{(x + 2)^{2}} > 0;\forall x \in \lbrack - 1;1brack

    \Rightarrow \max_{\lbrack - 1;1brack}y = y(1) = \frac{1 - m^{2}}{3} = \frac{1}{4} \Leftrightarrow m = \pm \frac{1}{2}

    Vậy tích tất cả các giá trị của tham số m bằng - \frac{1}{4}.

  • Câu 4: Thông hiểu

    Đồ thị hàm số y = \frac{\sqrt{1 - x^{2}}}{x^{2} + 2x} có bao nhiêu đường tiệm cận?

    Tập xác định D = \lbrack - 1;1brack\backslash\left\{ 0 ight\}

    Vì tập xác định của hàm số không chứa - \infty và + \infty nên đồ thị hàm số không có đường tiệm cận ngang.

    Lại có: \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}} = - \infty \hfill \\ \mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}} = + \infty \hfill \\ \end{gathered} ight.. Vậy đồ thị hàm số có 1 đường tiệm cận đứng x = 0.

  • Câu 5: Thông hiểu

    Tìm điều kiện cần và đủ của tham số thực ủa tham số m để đường thẳng y = 3x + m - 2 cắt đồ thị y = (x - 1)^{3} tại ba điểm phân biệt là:

    Phương trình hoành độ giao điểm của hai đồ thị:

    (x - 1)^{3} = 3x + m - 2 \Leftrightarrow m = x^{3} - 3x^{2} + 1(*)

    (*) là phương trình hoành độ giao điểm của hai đồ thị (d):y = m,(C):y = x^{3} - 3x^{2} + 1

    Xét hàm số f(x) = x^{3} - 3x^{2} + 1 có

    f'(x) = 3x^{2} - 6x \Rightarrow f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.

    Bảng biến thiên

    Vậy theo yêu cầu bài toán \Leftrightarrow - 3 < m < 1

  • Câu 6: Nhận biết

    Trong không gian Oxyz, cho hai điểm A(2;3; - 1) và B( - 4;1;9). Tìm tọa độ vectơ \overrightarrow{AB} ?

    Ta có:

    \overrightarrow{AB} = ( - 4 - 2;1 - 3;9 + 1) = ( - 6; - 2;10)

    Vậy đáp án đúng là: \overrightarrow{AB} = ( - 6; - 2;10).

  • Câu 7: Nhận biết

    Trong không gian Oxyz, cho các điểm A(2;1;4),B( - 2;2;6),C(6;0; - 1). Tích \overrightarrow{AB}.\overrightarrow{AC} bằng:

    Ta có: \left\{ \begin{matrix} \overrightarrow{AB} = ( - 4;1; - 10) \\ \overrightarrow{AC} = (4; - 1; - 5) \\ \end{matrix} ight.. Khi đó \overrightarrow{AB}.\overrightarrow{AC} = 33.

  • Câu 8: Nhận biết

    Cho bảng tần số ghép nhóm dưới đây:

    Độ tuổi

    [50; 55)

    [55; 60)

    [60; 65)

    [65; 70)

    [70; 75)

    [75; 80)

    [80; 85)

    [85; 90)

    Tần số

    4

    7

    4

    6

    16

    12

    2

    0

    Hãy xác định khoảng biến thiên của mẫu số liệu ghép nhóm trên?

    Do nhóm số liệu [85; 90) có tần số là 0 nên ta sẽ chỉ xét đến nhóm số liệu [80; 85).

    Do đó: R = 85 – 50 = 35.

  • Câu 9: Thông hiểu

    Kết quả đo chiều cao của học sinh lớp 12A được ghi lại trong bảng như sau:

    Chiều cao

    [160; 164)

    [164; 168)

    [168; 172)

    [172; 176)

    [176; 180)

    Số học sinh

    3

    5

    8

    4

    1

    Độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho là:

    Ta có:

    Chiều cao

    [160; 164)

    [164; 168)

    [168; 172)

    [172; 176)

    [176; 180)

    Số học sinh

    3

    5

    8

    4

    1

    Giá trị đại diện

    162

    166

    170

    174

    178

    Chiều cao trung bình là:

    \overline{x} = \frac{3.162 + 5.166 + 8.170 + 4.174 + 1.178}{21} \approx 169

    Phương sai của mẫu số liệu ghép nhóm là:

    S^{2} = \frac{1}{21}\left( 3.162^{2} + 5.166^{2} + 8.170^{2} + 4.174^{2} + 1.178^{2} ight) - 169^{2} \approx 18,14

    Suy ra độ lệch chuẩn của mẫu số liệu ghép nhóm là: S \approx 4,26.

  • Câu 10: Thông hiểu

    Trong không gian Oxyz, cho điểm A( - 3; - 1; - 1). Hình chiếu vuông góc của A trên mặt phẳng (Oyz) là điểm A'(x;y;z). Khi đó giá trị 2x + y + z bằng:

    Hình chiếu vuông góc của A( - 3; - 1; - 1) trên mặt phẳng (Oyz) là A'(0; - 1; - 1)

    Suy ra 2x + y + z = - 2.

  • Câu 11: Nhận biết

    Cho đồ thị hàm số như sau:

    Đồ thị hàm số đã cho có phương trình tiệm cận đứng và tiệm cận ngang lần lượt là:

    Dựa vào đồ thị hàm số ta thấy phương trình tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là x = - 1;y = 1.

  • Câu 12: Thông hiểu

    Cho tứ diện ABCD và điểm G thỏa mãn \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0} (G là trọng tâm của tứ diện). Gọi G_{0} là giao điểm của GA và mặt phẳng (BCD). Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Vì G_{0} là giao điểm của GA và mặt phẳng (BCD) suy ra G_{0} là trọng tâm tam giác BCD suy ra \overrightarrow{G_{0}B} + \overrightarrow{G_{0}C} + \overrightarrow{G_{0}D} = \overrightarrow{0}

    Theo bài ra ta có: \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}

    \Leftrightarrow \overrightarrow{GA} + 3\overrightarrow{GG_{0}} + \overrightarrow{G_{0}B} + \overrightarrow{G_{0}C} + \overrightarrow{G_{0}D} = \overrightarrow{0}

    \Leftrightarrow \overrightarrow{GA} + 3\overrightarrow{GG_{0}} = \overrightarrow{0} \Leftrightarrow \overrightarrow{GA} = 3\overrightarrow{G_{0}G}

  • Câu 13: Thông hiểu

    Cho hàm số y = f(x) = \frac{x^{2} + 4x - 1}{x - 1} có đồ thị là (C). Xét tính đúng sai của các khẳng định sau:

    a) Số khoảng đồng biến và nghịch biến của hàm số là bằng nhau. Đúng||Sai

    b) Hàm số y = f(x) đạt cực đại tại điểm có toạ độ (−1; 2). Đúng||Sai

    c) Đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số y = f(x). Đúng||Sai

    d) Phương trình đường tiệm cận xiên của đồ thị hàm số y = f(x) là y = 2x + 5. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x) = \frac{x^{2} + 4x - 1}{x - 1} có đồ thị là (C). Xét tính đúng sai của các khẳng định sau:

    a) Số khoảng đồng biến và nghịch biến của hàm số là bằng nhau. Đúng||Sai

    b) Hàm số y = f(x) đạt cực đại tại điểm có toạ độ (−1; 2). Đúng||Sai

    c) Đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số y = f(x). Đúng||Sai

    d) Phương trình đường tiệm cận xiên của đồ thị hàm số y = f(x) là y = 2x + 5. Sai||Đúng

    Hàm số y = f(x) = \frac{x^{2} + 4x - 1}{x - 1} có tập xác định D\mathbb{= R}\backslash\left\{ 1 ight\}

    Ta có: y' = \frac{x^{2} - 2x - 3}{(x - 1)^{2}} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    Bảng biến thiên

    a) Đúng: Hàm số đồng biến trên các khoảng (−∞; -1) và (3;+∞) và nghịch biến trên các khoảng (−1;1) và (1;3) .

    b) Đúng: Đồ thị hàm số đạt cực đại tại điểm (−1;2)

    c) Đúng: Xét \lim_{x ightarrow 1^{-}}y = - \infty;\lim_{x ightarrow 1^{+}}y = + \infty nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f(x) = \frac{x^{2} + 4x - 1}{x - 1}.

    d) Sai: Xét \lim_{x ightarrow \infty}\left\lbrack y - (x + 5) ightbrack = \lim_{x ightarrow \infty}\left\lbrack \frac{4}{x - 1} ightbrack = 0 nên đường thẳng y = x + 5 là tiệm cận xiên của đồ thị hàm số y = f(x) = \frac{x^{2} + 4x - 1}{x - 1}.

  • Câu 14: Vận dụng

    Một bể bơi chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng đồ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.

    a) Sau t phút khối lượng muối trong bể là 750t (gam). Đúng||Sai

    b) Nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là f(t) = \frac{30t}{200 - t} . Sai||Đúng

    c) Xem y = f(t) là một hàm số xác định trên nửa khoảng \lbrack 0; + \infty) , tiệm cận ngang của đồ thị hàm số đó có phương trình là y = 30 . Đúng||Sai

    d) Khi t ngày càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Đúng||Sai

    Đáp án là:

    Một bể bơi chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng đồ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.

    a) Sau t phút khối lượng muối trong bể là 750t (gam). Đúng||Sai

    b) Nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là f(t) = \frac{30t}{200 - t} . Sai||Đúng

    c) Xem y = f(t) là một hàm số xác định trên nửa khoảng \lbrack 0; + \infty) , tiệm cận ngang của đồ thị hàm số đó có phương trình là y = 30 . Đúng||Sai

    d) Khi t ngày càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Đúng||Sai

    Sau t phút, khối lượng muối trong bể là 25.30.t = 750t (gam)

    Thể tích của lượng nước trong bể là 5000 + 25t (lít).

    Vậy nồng độ muối sau t phút là: f(t) = \frac{750t}{5000 + 25t} = \frac{30t}{200 + t} (gam/lít).

    Ta có \lim_{t ightarrow + \infty}f(t) = \lim_{t ightarrow + \infty}\frac{30t}{200 + t} = \lim_{x ightarrow + \infty}\left( 30 - \frac{6000}{200 + t} ight) = 30

    Vậy đường thẳng y = 30 là tiệm cận ngang của đồ thị hàm số f(t):

    Ta có đồ thị hàm số y = f(t) nhận đường thẳng y = 30 làm đường tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít).

    Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ nước muối bơm vào bể.

    a) Đúng. b) Sai. c) Đúng. d) Đúng.

  • Câu 15: Thông hiểu

    Trong không gian Oxyz , cho vectơ \overrightarrow{OA} = (2; - 1;5),B(5; - 5;7). Xét sự đúng sai của các khẳng định sau:

    a) Tọa độ của điểm A là (2; - 1;5). Đúng||Sai

    b) Gọi C(a;b;c) thỏa mãn ∆ABC nhận G(1;1;1) làm trọng tâm. Khi đó a + b + c = - 4 . Đúng||Sai

    c) Nếu A;B;M(x;y;1) thẳng hàng thì tổng x + y = 3 . Đúng||Sai

    d) Cho N \in (Oxy) để ∆ABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3. Sai||Đúng

    Đáp án là:

    Trong không gian Oxyz , cho vectơ \overrightarrow{OA} = (2; - 1;5),B(5; - 5;7). Xét sự đúng sai của các khẳng định sau:

    a) Tọa độ của điểm A là (2; - 1;5). Đúng||Sai

    b) Gọi C(a;b;c) thỏa mãn ∆ABC nhận G(1;1;1) làm trọng tâm. Khi đó a + b + c = - 4 . Đúng||Sai

    c) Nếu A;B;M(x;y;1) thẳng hàng thì tổng x + y = 3 . Đúng||Sai

    d) Cho N \in (Oxy) để ∆ABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3. Sai||Đúng

    a) Ta có:

    Tọa độ của điểm A là (2; - 1;5).

    b) G là trọng tâm tam giác ABC

    \Leftrightarrow \left\{ \begin{matrix}1 = \dfrac{2 + 5 + x_{C}}{3} \\1 = \dfrac{- 1 - 5 + y_{C}}{3} \\1 = \dfrac{5 + 7 + x_{C}}{3} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x_{C} = - 4 \\y_{C} = 9 \\x_{C} = - 9 \\\end{matrix} ight.\ \Rightarrow C( - 4;9; - 9)

    \Rightarrow a + b + c = - 4

    c) Ta có: \overrightarrow{AB} = (3; - 4;2);\overrightarrow{AC} = (x - 2;y + 1; - 4)

    Ba điểm A, B, M thằng hàng khi và chỉ khi

    \overrightarrow{AM} = k\overrightarrow{AB} \Leftrightarrow \left\{ \begin{matrix} x - 2 = 3k \\ y + 1 = k.( - 4) \\ - 4 = k.2 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = - 4 \\ y = 7 \\ k = - 2 \\ \end{matrix} ight.

    Suy ra x + y = 3

    d) Ta có: N \in (Oxy) \Rightarrow N = (x;y;0)

    \Rightarrow \overrightarrow{AN} = (x - 2;y + 1; - 5),\overrightarrow{AB} = (3; - 4;2)

    Ta có ∆ABN vuông cân tại A \Leftrightarrow \left\{ \begin{matrix} AN\bot AB(*) \\ AN = AB(**) \\ \end{matrix} ight.

    Từ (*) \Leftrightarrow \overrightarrow{AN}\bot\overrightarrow{AB} \Leftrightarrow 3(x - 2) - 4(y + 1) - 10 = 0

    \Leftrightarrow 3x - 4y = 20 \Leftrightarrow y = \frac{3}{4}x - 5

    Từ (**) AN^{2} = AB^{2} \Leftrightarrow (x - 2)^{2} + (y + 1)^{2} + 25 = 9 + 16 + 4

    \Leftrightarrow (x - 2)^{2} + \left( \frac{3x}{4} - 4 ight)^{2} = 4 \Leftrightarrow x = \frac{16}{5}

    \Rightarrow y = - \frac{13}{5} \Rightarrow N\left( \frac{16}{5}; - \frac{13}{5};0 ight)

    Vậy x_{N} + y_{N} = \frac{3}{5}

  • Câu 16: Thông hiểu

    Cho mẫu số liệu ghép nhóm về chiều cao (đơn vị: cm) của cây trong vườn nghiên cứu như sau:

    Chiều cao

    [40; 45)

    [45; 50)

    [50; 55)

    [55; 60)

    [60; 65)

    [65; 70)

    Số cây

    5

    10

    7

    9

    7

    4

    Xét tính đúng sai của các khẳng định sau:

    a) Nhóm [45; 50) có tần số tích luỹ là 15. Đúng||Sai

    b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 30. Đúng||Sai

    c) Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \frac{3n}{4} là nhóm [55; 60). Sai||Đúng

    d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là Q_{3} > 61. Sai||Đúng

    Đáp án là:

    Cho mẫu số liệu ghép nhóm về chiều cao (đơn vị: cm) của cây trong vườn nghiên cứu như sau:

    Chiều cao

    [40; 45)

    [45; 50)

    [50; 55)

    [55; 60)

    [60; 65)

    [65; 70)

    Số cây

    5

    10

    7

    9

    7

    4

    Xét tính đúng sai của các khẳng định sau:

    a) Nhóm [45; 50) có tần số tích luỹ là 15. Đúng||Sai

    b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 30. Đúng||Sai

    c) Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \frac{3n}{4} là nhóm [55; 60). Sai||Đúng

    d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là Q_{3} > 61. Sai||Đúng

    a) Đúng: Nhóm [45;50) có tần số tích luỹ là 5 + 10 = 15.

    b) Đúng: Khoảng biến thiên là 70 – 40 = 30

    c) Sai: Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \frac{n}{2} = 31,5 là nhóm [60; 65).

    d) Sai: Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \frac{n}{2} = 31,5 là nhóm [60; 65).

    Đầu mút trái, độ dài và tần số của nhóm [60; 65) lần lượt là s = 60;h = 5;n_{2} = 7.

    Tần số tích luỹ của nhóm liền trước là cf_{4} = 31 nên tứ phân vị thứ ba là:

    Q_{1} = 60 + \left( \frac{31,5 - 31}{7} ight).5 \approx 60,36

  • Câu 17: Thông hiểu

    Tìm giá trị của tham số m để hàm số y = \frac{1}{3}x^{3} - (m + 1)x^{2} + \left( m^{2} + 2m ight)x - 3 nghịch biến trên khoảng ( - 1;1)

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Tìm giá trị của tham số m để hàm số y = \frac{1}{3}x^{3} - (m + 1)x^{2} + \left( m^{2} + 2m ight)x - 3 nghịch biến trên khoảng ( - 1;1)

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Vận dụng

    Cho hàm số y = f(x) liên tục trên tập số thực và có bảng biến thiên như sau:

    Đặt g(x) = \left| f(x + 1) + might| với m là tham số. Tìm điều kiện của tham số m để hàm số y = g(x) có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) liên tục trên tập số thực và có bảng biến thiên như sau:

    Đặt g(x) = \left| f(x + 1) + might| với m là tham số. Tìm điều kiện của tham số m để hàm số y = g(x) có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Vận dụng

    Để uốn 4m thanh kim loại thành hình như sau:

    Gọi r bán kính của nửa đường tròn. Tìm r(m) để diện tích tạo thành đạt giá trị lớn nhất?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Để uốn 4m thanh kim loại thành hình như sau:

    Gọi r bán kính của nửa đường tròn. Tìm r(m) để diện tích tạo thành đạt giá trị lớn nhất?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Thông hiểu

    Trong không gian, cho hai vectơ \overrightarrow{a} và \overrightarrow{b} có cùng độ dài bằng 6. Biết độ dài của vectơ \overrightarrow{a} + 2\overrightarrow{b} bằng 6\sqrt{3}. Biết số đo góc giữa hai vectơ \overrightarrow{a} và \overrightarrow{b} là x độ. Giá trị của x là bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong không gian, cho hai vectơ \overrightarrow{a} và \overrightarrow{b} có cùng độ dài bằng 6. Biết độ dài của vectơ \overrightarrow{a} + 2\overrightarrow{b} bằng 6\sqrt{3}. Biết số đo góc giữa hai vectơ \overrightarrow{a} và \overrightarrow{b} là x độ. Giá trị của x là bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Vận dụng

    Thống kê tổng số giờ nắng trong tháng 9 tại khu vực A trong các năm từ 2004 đến 2023 được thống kê như sau:

    111,6

    134,9

    130,3

    134,2

    140,9

    109,3

    154,4

    156,3

    116,1

    96,7

    105,2

    80,8

    80,8

    110

    109

    139

    145

    161

    126

    114

    Lập bảng tần số ghép nhóm với nhóm đầu tiên là [80; 98) và độ dài nhóm bằng 18. Tính sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Thống kê tổng số giờ nắng trong tháng 9 tại khu vực A trong các năm từ 2004 đến 2023 được thống kê như sau:

    111,6

    134,9

    130,3

    134,2

    140,9

    109,3

    154,4

    156,3

    116,1

    96,7

    105,2

    80,8

    80,8

    110

    109

    139

    145

    161

    126

    114

    Lập bảng tần số ghép nhóm với nhóm đầu tiên là [80; 98) và độ dài nhóm bằng 18. Tính sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Vận dụng cao

    Cho hàm số bậc ba f\left( x ight) = a{x^3} + b{x^2} + cx + d có đồ thị như hình vẽ:

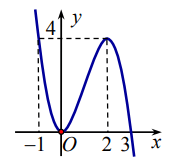
    Tìm giá trị m để đồ thị hàm số có 3 tiệm cận đứng

    Có bao nhiêu giá trị của m để hàm số g\left( x ight) = \frac{{\left( {{x^2} - 2mx + {m^2} + m + 1} ight)\sqrt {{x^2} - 3x} }}{{\left( {x - 4} ight)\left[ {{f^2}\left( x ight) - 4f\left( x ight)} ight]}} có 3 tiệm cận đứng?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số bậc ba f\left( x ight) = a{x^3} + b{x^2} + cx + d có đồ thị như hình vẽ:

    Tìm giá trị m để đồ thị hàm số có 3 tiệm cận đứng

    Có bao nhiêu giá trị của m để hàm số g\left( x ight) = \frac{{\left( {{x^2} - 2mx + {m^2} + m + 1} ight)\sqrt {{x^2} - 3x} }}{{\left( {x - 4} ight)\left[ {{f^2}\left( x ight) - 4f\left( x ight)} ight]}} có 3 tiệm cận đứng?

    Chỗ nhập nội dung câu trả lời tự luận
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi HK1 Toán 12 Kết nối tri thức Đề 1 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 23 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi HK1 Toán 12 Kết nối tri thức Đề 1
Thời gian còn lại 90:00 Số câu đã làm 0/22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập