Lớp 12 Toán 12 - Kết nối tri thức

Đề thi HK1 Toán 12 Kết nối tri thức Đề 2

Mô tả thêm: Đề thi HK1 Toán 12 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức toán 12 kết nối tri thức.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 22 câu
  • Số điểm tối đa: 22 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng ( - \infty; + \infty). Đồ thị hàm số y = f'(x) như hình vẽ:

    Hàm số y = f(x) nghịch biến trên khoảng nào trong các khoảng nào sau đây?

    Hàm số y = f(x) nghịch biến khi f'(x) \leq 0 \Leftrightarrow x \in (0;3)

    Vậy hàm số nghịch biến trên khoảng (0;3).

  • Câu 2: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Giá trị cực đại của hàm số đã cho bằng:

    Quan sát bảng biến thiên dễ thấy giá trị cực đại của hàm số đã cho bằng 3.

  • Câu 3: Thông hiểu

    Cho hàm số y = \frac{x + m}{x + 1} (với m là tham số thực) thỏa mãn \max_{\lbrack 1;2brack}y + \min_{\lbrack 1;2brack}y = \frac{16}{3}. Mệnh đề nào sau đây đúng?

    Ta có: y' = \frac{1 - m}{(x + 1)^{2}}

    TH1: m = 1 \Rightarrow y = 1 loại

    TH2: m > 1 khi đó \max_{\lbrack 1;2brack}y = \frac{1 + m}{2};\min_{\lbrack 1;2brack}y = \frac{2 + m}{3}

    \max_{\lbrack 1;2brack}y + \min_{\lbrack 1;2brack}y = \frac{1 + m}{2} + \frac{2 + m}{3} = \frac{16}{3} \Leftrightarrow m = 5

    Suy ra đáp án cần tìm là m > 4.

  • Câu 4: Nhận biết

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash\left\{ - 1 ight\} liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

    Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

    Từ bảng biến thiên ta thấy:

    \lim_{x ightarrow - 1^{+}}y = - \infty suy ra x = - 1 là tiệm cận đứng.

    \lim_{x ightarrow - \infty}y = 2 suy ra y = 2 là tiệm cận ngang

    \lim_{x ightarrow - \infty}y = - 1 suy ra y = - 1 là tiệm cận ngang

    Vậy đồ thị hàm số đã cho có tất cả ba đường tiệm cận.

  • Câu 5: Nhận biết

    Đồ thị của hàm số nào có dạng như hình vẽ sau đây?

    Ta thấy hình vẽ là đồ thị của hàm bậc ba có hệ số a > 0 nên hàm số cần tìm là y = x^{3} - 3x - 1.

  • Câu 6: Nhận biết

    Trong không gian Oxyz, cho điểm M(1;0;2). Mệnh đề nào sau đây đúng?

    Vì tọa độ điểm M(1;0;2) có x = 1;y = 0;z = 2 nên M \in (Oxz).

  • Câu 7: Nhận biết

    Trong không gian hệ trục tọa độ Oxyzcho \overrightarrow{u} = 2\overrightarrow{i} + \overrightarrow{k}. Khi đó tọa độ \overrightarrow{u} với hệ Oxyz là:

    Ta có: \overrightarrow{i} = (1;0;0);\overrightarrow{j} = (0;1;0);\overrightarrow{k} = (0;0;1)

    \overrightarrow{u} = x\overrightarrow{i} + y\overrightarrow{j} + z\overrightarrow{k} \Leftrightarrow \overrightarrow{u} = (x;y;z)

    Lại có \overrightarrow{u} = 2\overrightarrow{i} + \overrightarrow{k} \Leftrightarrow \overrightarrow{u} = (2;0;1)

  • Câu 8: Nhận biết

    Gọi O là tâm của hình lập phương ABCD.A'B'C'D'. Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Theo quy tắc hình hộp ta có: \overrightarrow{AC'} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'}

    Vì O là trung điểm của AC' suy ra \overrightarrow{AO} = \frac{1}{2}\overrightarrow{AC'} = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} ight)

  • Câu 9: Thông hiểu

    Trong không gian hệ trục tọa độ Oxyz, cho hai vectơ \overrightarrow{a} = (m;2;4),\overrightarrow{b} = (1;n;2) cùng phương. Tìm cặp số thực (m;n)?

    Ta có hai vectơ \overrightarrow{a} = (m;2;4),\overrightarrow{b} = (1;n;2) cùng phương

    \Leftrightarrow \frac{m}{1} = \frac{2}{n} = \frac{4}{2} \Leftrightarrow \left\{ \begin{matrix} m = 2 \\ n = 1 \\ \end{matrix} ight.

    Vậy (m;n) = (2;1).

  • Câu 10: Thông hiểu

    Trong không gian tọa độ Oxyz, cho hai điểm A(1;2;0),B(2; - 1;1). Tìm tọa độ điểm C có hoành độ dương thuộc trục Ox sao cho tam giác ABC vuông tại C?

    Ta có: C có hoành độ dương thuộc trục Ox \Rightarrow C(x;0;0);x > 0

    Theo bài ra ta có: \left\{ \begin{matrix} \overrightarrow{AC} = (x - 1; - 2;0) \\ \overrightarrow{BC} = (x - 2;1; - 1) \\ \end{matrix} ight. và tam giác ABC vuông tại C nên

    \Leftrightarrow \overrightarrow{AC}.\overrightarrow{BC} = 0 \Leftrightarrow (x - 1)(x - 2) - 2 = 0

    \Leftrightarrow x^{2} - 3x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0(L) \\ x = 3(tm) \\ \end{matrix} ight.

    Vậy C(3;0;0)

  • Câu 11: Nhận biết

    Cho bảng thống kê chiều cao của học sinh nữ lớp 12A như sau:

    Chiều cao(cm)

    [155; 160)

    [160; 165)

    [165; 170)

    [170; 175)

    [175; 180)

    [180; 185)

    Số học sinh

    2

    7

    12

    3

    0

    1

    Một học sinh có nhận xét như sau: Chênh lệch chiều cao của các bạn trong lớp không vượt quá m (cm). Hãy xác định giá trị của m để nhận xét của học sinh đó là đúng?

    Ta có: R = 185 – 55 = 30

    Vậy giá trị của m = 30.

  • Câu 12: Thông hiểu

    Cho mẫu số liệu ghép nhóm như sau:

    Đối tượng

    [3; 5)

    [5; 7)

    [7; 9)

    [9; 11)

    [11; 13)

    Tần số

    6

    7

    6

    6

    5

    Kết luận nào dưới đây đúng?

    Ta có:

    Đối tượng

    [3; 5)

    [5; 7)

    [7; 9)

    [9; 11)

    [11; 13)

    Giá trị đại diện

    4

    6

    8

    10

    12

    Tần số

    6

    7

    6

    6

    5

    Giá trị trung bình là:

    \overline{x} = \frac{6.4 + 7.6 + 6.8 + 6.10 + 5.12}{30} = 7,8

    Phương sai của mẫu số liệu ghép nhóm là:

    S^{2} = \frac{1}{30}\left( 6.4^{2} + 7.6^{2} + 6.8^{2} + 6.10^{2} + 5.12^{2} ight) - 7,8^{2} = 7,56

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    S = \sqrt{S^{2}} = \sqrt{7,56} \approx 2,75.

    Vậy kết luận đúng là: \overline{x} = 7,8;S \approx 2,75.

  • Câu 13: Nhận biết

    Cho hàm số y = f(x) xác định trên \mathbb{R}\left\{ \pm 2 ight\} và có bảng biến thiên như sau:

    Xét tính đúng sai của các khẳng định sau.

    a) Hàm số không có điểm cực trị. Đúng||Sai

    b) \lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty. Sai||Đúng

    c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

    d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x) xác định trên \mathbb{R}\left\{ \pm 2 ight\} và có bảng biến thiên như sau:

    Xét tính đúng sai của các khẳng định sau.

    a) Hàm số không có điểm cực trị. Đúng||Sai

    b) \lim_{x ightarrow ( - 2)^{-}}f(x) = + \infty. Sai||Đúng

    c) Đồ thị hàm số có đúng 1 tiệm cận ngang. Đúng||Sai

    d) Đồ thị hàm số có đúng 1 tiệm cận đứng. Sai||Đúng

    Dựa vào bảng biến thiên ta thấy

    a) Hàm số không có điểm cực trị.

    b) lim \lim_{x ightarrow ( - 2)^{-}}f(x) = - 10.

    c) \lim_{x ightarrow \pm \infty}f(x) = 0. Suy ra đồ thị có đúng 1 đường tiệm cận ngang là y = 0.

    d) \lim_{x ightarrow ( - 2)^{+}}f(x) = + \infty và \lim_{x ightarrow 2^{+}}f(x) = + \infty nên đồ thị hàm số có đúng 2 đường tiệm cận đứng x = \pm 2.

  • Câu 14: Thông hiểu

    Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích 1800m^{3} và chiều sâu 2m (như hình vẽ).

    Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

    Xét tính đúng sai của các khẳng định sau:

    a) Thể tích bể chứa được tính theo công thức V = 2x^{2}y . Sai|| Đúng

    b) Mối liên hệ giữa x và y là y = \frac{900}{x} . Đúng||Sai

    c) Tổng diện tích mặt bên của bể tính theo x, y là S = 4(x + y) . Đúng||Sai

    d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là 40m . Sai|| Đúng

    Đáp án là:

    Người ta muốn xây một bể chứa có dạng hình hộp chữ nhật, thể tích 1800m^{3} và chiều sâu 2m (như hình vẽ).

    Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Gọi x (m) và y (m) là hai kích thước của mặt đáy.

    Xét tính đúng sai của các khẳng định sau:

    a) Thể tích bể chứa được tính theo công thức V = 2x^{2}y . Sai|| Đúng

    b) Mối liên hệ giữa x và y là y = \frac{900}{x} . Đúng||Sai

    c) Tổng diện tích mặt bên của bể tính theo x, y là S = 4(x + y) . Đúng||Sai

    d) Để tổng chi phí xây dựng (bao gồm mặt đáy và mặt bên) nhỏ nhất thì cần chọn chiều dài là 40m . Sai|| Đúng

    a) Thể tích của bể là V = B.h = xy.\ h.

    b) Với V = xy.h \Rightarrow 1800 = xy.2 \Rightarrow xy = \frac{1800}{2} = 900.

    c) Tổng diện tích mặt bên gồm 4 hình chữ nhật (trước, sau, trái, phải) là:

    \ S = 2x + 2x + 2y + 2y = 4x + 4y = 4(x + y)

    d) Tổng diện tích của bể là: 4x + 4y + xy = 4x + 4.\frac{900}{x} + 900

    Vì chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể nên chi phí cần có là 4x + 4.\frac{900}{x} + 2.900

    Đặt f(x) = 4x + 4.\frac{900}{x} + 1800 ta có: f'(x) = 4 - \frac{3600}{x^{2}} \Rightarrow f'(x) = 0 \Leftrightarrow x = 30 ta có bảng biến thiên như sau:

    Với x = 30m;y = 30 m và thì chi phí xây dựng bể là thấp nhất.

  • Câu 15: Thông hiểu

    Tìm hiểu thời gian (đơn vị: giờ) sử dụng điện thoại di động của một nhóm bạn trẻ thu được kết quả sau như sau:

    Thời gian

    [0; 5)

    [5; 10)

    [10; 15)

    [15; 20)

    [20; 25)

    [25; 30)

    Số bạn

    2

    6

    8

    9

    3

    2

    Xác định tính đúng sai của các đáp án dưới đây?

    a) Khoảng biến thiên của mẫu số liệu ghép nhóm này là 25. Sai||Đúng

    b) Nhóm chứa tứ phân vị thứ 3 là [15; 20). Đúng||Sai

    c) Số trung bình của thống kê là 10. Sai||Đúng

    d) Khoảng tứ phân của mẫu số liệu ghép nhóm này lớn hơn 10. Sai||Đúng

    Đáp án là:

    Tìm hiểu thời gian (đơn vị: giờ) sử dụng điện thoại di động của một nhóm bạn trẻ thu được kết quả sau như sau:

    Thời gian

    [0; 5)

    [5; 10)

    [10; 15)

    [15; 20)

    [20; 25)

    [25; 30)

    Số bạn

    2

    6

    8

    9

    3

    2

    Xác định tính đúng sai của các đáp án dưới đây?

    a) Khoảng biến thiên của mẫu số liệu ghép nhóm này là 25. Sai||Đúng

    b) Nhóm chứa tứ phân vị thứ 3 là [15; 20). Đúng||Sai

    c) Số trung bình của thống kê là 10. Sai||Đúng

    d) Khoảng tứ phân của mẫu số liệu ghép nhóm này lớn hơn 10. Sai||Đúng

    Ta có

    Thời gian

    [0; 5)

    [5; 10)

    [10; 15)

    [15; 20)

    [20; 25)

    [25; 30)

    Giá trị đại diện

    2,5

    7,5

    12,5

    17,5

    22,5

    17,5

    Số bạn

    2

    6

    8

    9

    3

    2

    a) Sai: Khoảng biến thiên của mẫu số liệu ghép nhóm là R = 30 - 0 = 30.

    b) Đúng:

    Vì 16 < \frac{3n}{4} = \frac{3.30}{4} = \frac{90}{4} = 22,5 < 25 nên nhóm chứa tứ phân vị thứ 3 là [15;20).

    c) Sai: Thời gian sử dụng điện thoại trung bình là:

    \overline{x} = \frac{2.2,5 + 6.7,5 + 8.12,5 + 9.17,5 + 3.22,5 + 2.27,5}{30} = \frac{43}{3} \approx 14,3

    d) Sai: Ta có: \frac{n}{4} = 7,5;\frac{n}{2} = 15;\frac{3n}{4} = 22,5

    \left\{ \begin{matrix} {Q_1} = 5 + \dfrac{{\dfrac{{30}}{4} - 2}}{6}.5 = 9,58 \hfill \\ {Q_3} = 15 + \dfrac{{\dfrac{{90}}{4} - 16}}{9}.5 \approx 18,61 \hfill \\ \end{matrix} ight. \Rightarrow \Delta Q = {Q_3} - {Q_1} \approx 9,03 < 10

  • Câu 16: Vận dụng

    Trong không gian Oxyz cho hai điểm M(2;3; - 1),N( - 1;1;1). Xác định tính đúng sai của từng phương án dưới đây:

    a) Hình chiếu của điểm M trên trục Oy có tọa độ là (−2;3;1). Sai||Đúng

    b) Gọi E là điểm đối xứng của điểm M qua N. Tọa độ của điểm E là ( - 4; - 1;3). Đúng||Sai

    c) Cho P(1;m - 1;3), tam giác MNP vuông tại N khi và chỉ khi m = 1. Đúng||Sai

    d) Điểm I(a;b;c) nằm trên mặt phẳng (Oxy) thỏa mãn T = \left| 3\overrightarrow{IM} - \overrightarrow{IN} ight| đạt giá trị nhỏ nhất. Khi đó 2a + b + c = 9. Sai||Đúng

    Đáp án là:

    Trong không gian Oxyz cho hai điểm M(2;3; - 1),N( - 1;1;1). Xác định tính đúng sai của từng phương án dưới đây:

    a) Hình chiếu của điểm M trên trục Oy có tọa độ là (−2;3;1). Sai||Đúng

    b) Gọi E là điểm đối xứng của điểm M qua N. Tọa độ của điểm E là ( - 4; - 1;3). Đúng||Sai

    c) Cho P(1;m - 1;3), tam giác MNP vuông tại N khi và chỉ khi m = 1. Đúng||Sai

    d) Điểm I(a;b;c) nằm trên mặt phẳng (Oxy) thỏa mãn T = \left| 3\overrightarrow{IM} - \overrightarrow{IN} ight| đạt giá trị nhỏ nhất. Khi đó 2a + b + c = 9. Sai||Đúng

    a) Sai: Hình chiếu của điểm M trên trục Oy có tọa độ là (0;3;0)

    b) Đúng: Vì N là trung điểm của ME

    \Leftrightarrow \left\{ \begin{matrix}- 1 = \dfrac{2 + x_{E}}{2} \\1 = \dfrac{3 + y_{E}}{2} \\1 = \dfrac{- 1 + z_{E}}{2} \\\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x_{E} = - 4 \\y_{E} = - 1 \\z_{E} = 3 \\\end{matrix} \Rightarrow E( - 4; - 1;3) ight.\ ight..

    c) Đúng: Ta có \overrightarrow{NM} = (3;2; - 2);\overrightarrow{NP} = (2;m - 2;2).

    \bigtriangleup MNP vuông tại N \Leftrightarrow\overrightarrow{NM}.\overrightarrow{NP} = 0

    \Leftrightarrow 3.2 + 2.(m - 2) + ( - 2).2 = 0 \Leftrightarrow m = 1.

    d) Sai.

    Gọi J(x;y;z) thỏa 3\overrightarrow{JM} - \overrightarrow{JN} = \overrightarrow{0}

    \Leftrightarrow \left\{ \begin{matrix}3(2 - x) - ( - 1 - x) = 0 \\3(3 - y) - (1 - y) = 0 \\3( - 1 - z) - (1 - z) = 0 \\\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x = \dfrac{7}{2} \\y = 4 \\z = - 2 \\\end{matrix} ight.\ ight.

    Suy ra J\left( \frac{7}{2};4; - 2 ight).

    Khi đó T = |3\overrightarrow{IM} - \overrightarrow{IN}| = |3\overrightarrow{IJ} + 3\overrightarrow{JM} - \overrightarrow{IJ} - \overrightarrow{JN}| = |2\overrightarrow{IJ}| = 2IJ.

    T đạt giá trị nhỏ nhất khi và chỉ khi I là hình chiếu của J trên (Oxy)

    \Leftrightarrow I\left( \frac{7}{2};4;0 ight).

    Vậy a = \frac{7}{2};b = 4;c = 0.

    Suy ra 2a+b+c=11

  • Câu 17: Thông hiểu

    Cho hàm số y = \frac{mx - 18}{x -2m}. Giả sử S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng (2; + \infty). Xác định tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \frac{mx - 18}{x -2m}. Giả sử S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng (2; + \infty). Xác định tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Vận dụng

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Vận dụng

    Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.

    Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900(km/h) lên 920(km/h), trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900(km/h) và 920(km/h) lần lượt biểu diễn bởi hai vectơ \overrightarrow{F_{1}} và \overrightarrow{F_{2}} với \overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight). Tính giá trị của k (Làm tròn kết quả đến chữ số thập phân thứ hai).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.

    Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900(km/h) lên 920(km/h), trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900(km/h) và 920(km/h) lần lượt biểu diễn bởi hai vectơ \overrightarrow{F_{1}} và \overrightarrow{F_{2}} với \overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight). Tính giá trị của k (Làm tròn kết quả đến chữ số thập phân thứ hai).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Vận dụng

    Kết quả điều tra thu nhập (triệu đồng/năm) năm 2023 của một số hộ gia đình tại địa phương được ghi lại trong bảng sau:

    Tổng thu nhập

    [200; 250)

    [250; 300)

    [300; 350)

    [350; 400)

    [400; 450)

    Số hộ gia đình

    24

    62

    34

    21

    9

    Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Kết quả điều tra thu nhập (triệu đồng/năm) năm 2023 của một số hộ gia đình tại địa phương được ghi lại trong bảng sau:

    Tổng thu nhập

    [200; 250)

    [250; 300)

    [300; 350)

    [350; 400)

    [400; 450)

    Số hộ gia đình

    24

    62

    34

    21

    9

    Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Vận dụng cao

    Cho hàm số y = f\left( x ight). Hàm số y = f'\left( x ight) có đồ thị như hình vẽ dưới đây:

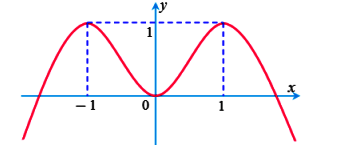
    Bất phương trình nghiệm đúng khi và chỉ khi

    Bất phương trình \frac{{f\left( x ight)}}{{36}} - \frac{{\sqrt {x + 3} - 2}}{{x - 1}} > m nghiệm đúng với mọi x \in \left( {0;1} ight) khi và chỉ khi

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f\left( x ight). Hàm số y = f'\left( x ight) có đồ thị như hình vẽ dưới đây:

    Bất phương trình nghiệm đúng khi và chỉ khi

    Bất phương trình \frac{{f\left( x ight)}}{{36}} - \frac{{\sqrt {x + 3} - 2}}{{x - 1}} > m nghiệm đúng với mọi x \in \left( {0;1} ight) khi và chỉ khi

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Vận dụng

    Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có tọa độ các đỉnh A(1;2; - 1),B(2; - 1;3),C( - 4;7;5). Gọi D(a;b;c) là chân đường phân giác trong của góc B trong tam giác ABC. Tính giá trị biểu thức W = a + b + 2c?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có tọa độ các đỉnh A(1;2; - 1),B(2; - 1;3),C( - 4;7;5). Gọi D(a;b;c) là chân đường phân giác trong của góc B trong tam giác ABC. Tính giá trị biểu thức W = a + b + 2c?

    Chỗ nhập nội dung câu trả lời tự luận
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi HK1 Toán 12 Kết nối tri thức Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 5 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi HK1 Toán 12 Kết nối tri thức Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập