Rút gọn biểu thức: ![]() với
với ![]() ta được kết quả là:
ta được kết quả là:
Ta có: .
Rút gọn biểu thức: ![]() với
với ![]() ta được kết quả là:
ta được kết quả là:
Ta có: .
Tính giá trị của biểu thức ![]() biết
biết ![]() ?
?
Ta có:
Một người học bắn cung tên bắn liên tục 4 mũi tên vào mục tiêu. Gọi ![]() là biến cố cung thủ bắn trúng lần thứ
là biến cố cung thủ bắn trúng lần thứ ![]() . Hãy mô tả biến cố bắn trúng mục tiêu ít nhất một lần qua các biến cố
. Hãy mô tả biến cố bắn trúng mục tiêu ít nhất một lần qua các biến cố ![]() .
.
Gọi M là biến cố bắn trúng mục tiêu ít nhất 1 lần
Khi đó là biến cố lần thứ
bắn không trúng mục tiêu.
Khi đó ta có:
Xác định các nghiệm phương trình ![]() rồi tính tổng tất cả các giá trị đó ta được kết quả là: 16/3
rồi tính tổng tất cả các giá trị đó ta được kết quả là: 16/3
(Kết quả ghi dưới dạng phân số tối giản a/b)
Xác định các nghiệm phương trình rồi tính tổng tất cả các giá trị đó ta được kết quả là: 16/3
(Kết quả ghi dưới dạng phân số tối giản a/b)
Điều kiện
Ta có:
Tổng tất cả các nghiệm của phương trình là: .
Gieo ngẫu nhiên một đồng tiền xu ba lần liên tiếp. Gọi D là biến cố có ít nhất hai lần gieo xuất hiện mặt sấp. Tìm biến cố đối của biến cố D?
Ta có:
Biến cố là biến cố có đúng một lần xuất hiện mặt sấp hoặc không có lần nào xuất hiện mặt sấp.
Cho hình lập phương ![]() . Tính
. Tính ![]() ?
?
Hình vẽ minh họa
Vì
Tam giác A’B’C’ vuông cân tại B’
Vậy .
Cho hình chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh bằng
là hình vuông cạnh bằng ![]() ,
, ![]() . Xác định độ lớn khoảng cách từ điểm
. Xác định độ lớn khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() ?
?
Hình vẽ minh họa
Gọi
Kẻ
Ta có:
Mà
Từ (*) và (**) suy ra
Từ (1) và (2) suy ra
Xét tam giác vuông tại
ta có:
Cho hình chóp tứ giác ![]() có
có ![]() và đáy là hình vuông. Chọn kết luận đúng?
và đáy là hình vuông. Chọn kết luận đúng?
Hình vẽ minh họa
Ta có:
Ta có:
Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC). Điểm I là:
Ta có:
Chứng minh tương tự ta được:
Vậy I là trực tâm của tam giác ABC.
Công thức nào tương ứng với đạo hàm cấp hai của hàm số ![]() ?
?
Ta có:
Cho hai động cơ hoạt động độc lập nhau. Xác suất để động cơ 1 chạy tốt là ![]() và xác suất để động cơ 2 chạy tốt là
và xác suất để động cơ 2 chạy tốt là ![]() . Tìm xác suất để có ít nhất một động cơ chạy tốt.
. Tìm xác suất để có ít nhất một động cơ chạy tốt.
Đáp án: 0,94
(Ghi đáp án dưới dạng số thập phân)
Cho hai động cơ hoạt động độc lập nhau. Xác suất để động cơ 1 chạy tốt là và xác suất để động cơ 2 chạy tốt là
. Tìm xác suất để có ít nhất một động cơ chạy tốt.
Đáp án: 0,94
(Ghi đáp án dưới dạng số thập phân)
Gọi A là biến cố có ít nhất một động cơ chạy tốt
B là biến cố chỉ có động cơ 1 chạy tốt.
Gọi C là biến cố chỉ có động cơ 2 là chạy tốt.
Gọi D là biến cố cả hai động cơ đều chạy tốt
Vậy
Cho hàm số ![]() với
với ![]() là tham số. Tìm tất cả các giá trị thực của tham số
là tham số. Tìm tất cả các giá trị thực của tham số ![]() để hàm số đã
để hàm số đã ![]() xác định với mọi
xác định với mọi ![]() ?
?
Hàm số xác định với mọi
khi và chỉ khi
Vậy
Tính số gia của hàm số ![]() tại điểm x0 = 2 ứng với số gia
tại điểm x0 = 2 ứng với số gia ![]()
Ta có:
Giả sử có bảy bông hoa khác nhau và ba lọ hoa khác nhau. Hỏi có bao nhiêu cách cắm ba bông hoa vào ba lọ đã cho (mỗi lọ cắm một bông)?
Số cách xếp bảy bông hoa khác nhau vào ba lọ hoa khác nhau là số chỉnh hợp chập 3 của 7 phần tử.
=> Có cách.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi AM, AN lần lượt là đường cao của tam giác SAB và tam giác SAD. Khẳng định nào dưới đây là khẳng định đúng?
Hình vẽ minh họa:
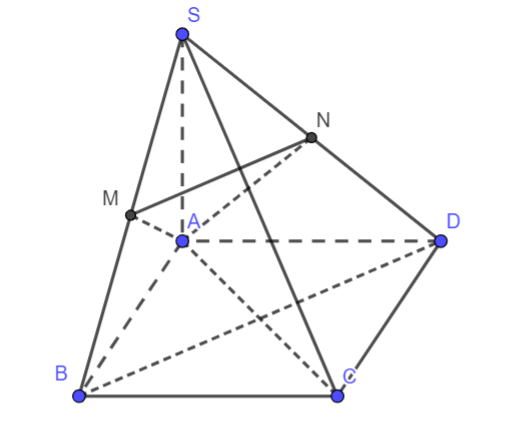
Ta có: SA ⊥ (ABCD) => SA ⊥ BC
Mà AB ⊥ BC => BC ⊥ (SAB)
=> BC ⊥ AE
Mà AM nằm trong mặt phẳng (SAB)
Xét tam giác SAB có:
AM ⊥ SB
Mà BC ⊥ AM => AM ⊥ (SBC) => AM ⊥ SC
Chứng minh tương tự ta được: AN ⊥ SC
=> SC ⊥ (AMN)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết: ![]() . Hai bên mặt SAB và SAD vuông tại a. Gọi μ là góc giữa hai đường thẳng SB và AC. Tính cosμ?
. Hai bên mặt SAB và SAD vuông tại a. Gọi μ là góc giữa hai đường thẳng SB và AC. Tính cosμ?
Hình vẽ minh họa:
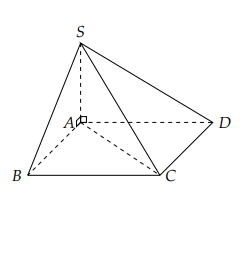
Ta có:
Ta lại có:
Tuấn làm một bài kiểm tra trắc nghiệm gồm 10 câu hỏi, mỗi câu gồm 4 phương án và chỉ có 1 phương án đúng. Mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ 2 điểm. Tuấn chọn ngẫu nghiên đáp án cho 10 câu hỏi. Xác suất để Tú thi được không quá 1 điểm?
Xác suất trả lời đúng trong một câu là:
Xác suất trả lời sai trong một câu là:
Gọi x là số câu Tuấn trả lời đúng.
Theo đều bài ra ta có Tuấn thi được không quá 1 điểm suy ra
Do đó Tuấn cần trả lời đúng không quá 3 câu
TH1: Học sinh trả lời đúng 3 câu:
TH2: Học sinh trả lời đúng 2 câu:
TH3: Học sinh trả lời đúng 1 câu:
TH4: Học sinh trả lời không đúng câu nào:
Vậy xác suất cần tìm là
Hàm số nào sau đây đồng biến trên ![]() ?
?
Do nên hàm số
đồng biến trên
.
Lớp 11A chọn ngẫu nhiên 1 học sinh trong lớp để tham gia hoạt động đoàn trường. Xét hai biến cố:
Biến cố A: “Học sinh đó là nam”
Biến cố B: “Học sinh đó là học sinh giỏi”
Khẳng định nào sau đây đúng khi mô tả biến cố ![]() ?
?
Ta có:
: Học sinh đó là học sinh nam hoặc là học sinh giỏi
Cho hai tam giác đều DAC và BAC lần lượt nằm trong hai mặt phẳng vuông góc với nhau. Gọi α là góc giữa hai mặt phẳng (DAB) và (DBC). Tính giá trị cos α.
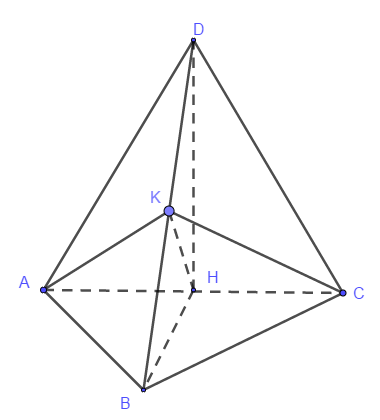
Giả sử cạnh của tam giác đều bằng 2a. Khi đó AB = AD = CB = CD = 2a
Gọi H là trung điểm của AC. Tam giác DAC đều suy ra DH ⊥ AC.
Tương tự BH ⊥ AC.
Ta có:
Gọi K là trung điểm của DB.
Ta có: ABD cân tại A nên
Và CBD cân tại C nên
Ta có:
Suy ra góc giữa hai mặt phẳng (DAB) và (DBC) là góc giữa hai đường thẳng AK và CK.
Ta có nên BDH vuông cân tại H.
Từ đó ta có:
Ta có: mà
Xét tam giác ACK có KH vừa là trung tuyến, vừa là đường cao nên tam giác ACK cân tại K.
Nên ta có: KH là phân giác của góc suy ra
Ta có:
Vậy
Quãng đường chuyển động của một ô tô được biểu diễn bằng phương trình ![]() , trong đó
, trong đó ![]() tính bằng mét và
tính bằng mét và ![]() tính bằng giây. Trong thời gian
tính bằng giây. Trong thời gian ![]() kể từ khi bắt đầu chuyển động, ô tô đạt vận tốc lớn nhất bằng bao nhiêu?
kể từ khi bắt đầu chuyển động, ô tô đạt vận tốc lớn nhất bằng bao nhiêu?
Kết quả: 28(m/s)
Quãng đường chuyển động của một ô tô được biểu diễn bằng phương trình , trong đó
tính bằng mét và
tính bằng giây. Trong thời gian
kể từ khi bắt đầu chuyển động, ô tô đạt vận tốc lớn nhất bằng bao nhiêu?
Kết quả: 28(m/s)
Ta có:
Suy ra vận tốc của chuyển động là
Dễ thấy hàm số là hàm số bậc hai có đồ thị dạng Parabol với hệ số
Ta có hoành độ đỉnh của Parabol là
Do đó
Vậy giá trị lớn nhất của vận tốc ô tô chuyển động trong 5 giây đầu là
Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành và mặt bên
là hình bình hành và mặt bên ![]() là tam giác vuông tại
là tam giác vuông tại ![]() . Tính số đo góc giữa hai đường thẳng
. Tính số đo góc giữa hai đường thẳng ![]() và
và ![]() .
.
Hình vẽ minh họa
Vì là hình bình hành nên
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng (ABCD) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
Hình vẽ minh họa:
Từ giả thiết ABCD là hình vuông và SB vuông góc với đáy
Ta có:
Cho hình chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh bằng
là hình vuông cạnh bằng ![]() ;
; ![]() . Gọi
. Gọi ![]() lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của ![]() trên các cạnh
trên các cạnh ![]() . Tính số đo góc giữa đường thẳng
. Tính số đo góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() .
.
Hình vẽ minh họa
Gọi
Ta có:
Ta có:
Viết phương trình tiếp tuyến của đồ thị hàm số ![]() song song với đường thẳng
song song với đường thẳng ![]() ?
?
Ta có:
Vì tiếp tuyến song song với nên hệ số góc bằng 3 nên gọi tọa độ tiếp điểm là
Khi đó
Với
Với
Để quyết định người chiến thắng cuộc thi người ta thực hiện gieo đồng thời ba con xúc xắc cân đối và đồng chất một vài lần. Người thắng cuộc nếu xuất hiện ít nhất 2 mặt 6 chấm. Tính xác suất để trong ba lần gieo, người đó thắng ít nhất 2 lần?
Xác suất để một con xúc xắc xuất hiện mặt 6 chấm là
Xác suất để người chơi thắng cuộc trong một lần gieo là
Xác suất để trong 3 lần gieo người đó thắng ít nhất hai lần là:
Một chất điểm chuyển động được biểu diễn bởi phương trình ![]() ,
, ![]() tính bằng giây,
tính bằng giây, ![]() tính bằng mét. Tại thời điểm gia tốc của chất điểm đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
tính bằng mét. Tại thời điểm gia tốc của chất điểm đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
Kết quả: 28 (m/s)
Một chất điểm chuyển động được biểu diễn bởi phương trình ,
tính bằng giây,
tính bằng mét. Tại thời điểm gia tốc của chất điểm đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
Kết quả: 28 (m/s)
Vận tốc tức thời là
Gia tốc tức thời của chất điểm là:
Vậy gia tốc đạt giá trị nhỏ nhất khi t = 3. Khi đó vận tốc của chất điểm là
Đầu mỗi tháng cô H gửi vào ngân hàng 4 triệu đồng với lãi suất kép là 0,5% mỗi tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì cô H có được số tiền cả lãi và gốc nhiều hơn 100 triệu, biết lãi suất không đổi trong quá trình gửi.
Ta có:
Giả sử sau n tháng sau anh A nhận được số tiền nhiều hơn 100 triệu, khi đó ta có:
Vậy cần ít nhất 24 tháng để cô H có được số tiền cả lãi và gốc nhiều hơn 100 triệu.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 600. Tính khoảng cách d từ điểm D đến mặt phẳng (SBC)
Hình vẽ minh họa
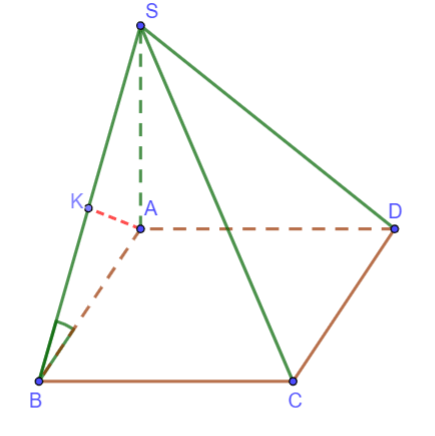
Ta có:
Ta có:
=>
Kẻ (1)
Ta có:
Từ (1) và (2) =>
Cho hai đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() . Chọn mệnh đề sai trong các mệnh đề dưới đây?
. Chọn mệnh đề sai trong các mệnh đề dưới đây?
Mệnh đề: “Nếu thì
.” Sai vì đường thẳng b có thể nằm trong mặt phẳng (Q).
Cho khối lăng trụ ![]() có
có ![]() , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm ![]() lên mặt phẳng
lên mặt phẳng ![]() là trung điểm
là trung điểm ![]() của
của ![]() . Biết
. Biết ![]() . Tính thể tích khối lăng trụ
. Tính thể tích khối lăng trụ ![]() ?
?
Hình vẽ minh họa:
Gọi lần lượt là hình chiếu của A trên BB’ và CC’
Theo đề bài ta có:
Dễ thấy nên tam giác
vuông tại A
Gọi H là trung điểm của
Ta lại có
Suy ra
Vậy
Số cách sắp xếp ![]() vào một dãy ghế dài sao cho hai đầu dãy ghế là vị trí của
vào một dãy ghế dài sao cho hai đầu dãy ghế là vị trí của ![]() và
và ![]() ?
?
Ta xếp A và G vào hai vị trí đầu dãy và có thể hoán đổi cho nhau nên ta có 2! cách xếp.
Xếp 5 người còn lại vào 5 vị trí giữa ta có 5! cách xếp.
Vậy ta có: 2!.5! = 240 cách xếp.
Tìm tập nghiệm của bất phương trình ![]() ?
?
Ta có:
Vậy tập nghiệm của bất phương trình là
Theo dự định số lượng thức ăn dự trữ của nông trại B sẽ hết sau 100 ngày, nhưng thực tế mức tiêu thụ của vật nuôi tăng thêm 4% mỗi ngày (ngày sau tăng 4% so với ngày trước đó). Hỏi lượng thức ăn dự trữ thực tế sẽ hết sau khoảng bao nhiêu ngày? (làm tròn đến hàng đơn vị)
Theo dự định, mỗi ngày lượng thức ăn tiêu thụ là: (lượng thức ăn)
Lượng thức ăn mà vật nuôi ăn hết ở ngày thứ k là: (lượng thức ăn)
Xác định số tự nhiên n nhỏ nhất để:
Cho khối lăng trụ tam giác đều ![]() có
có ![]() . Tính thể tích khối lăng trụ biết góc giữa mặt phẳng
. Tính thể tích khối lăng trụ biết góc giữa mặt phẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() .
.
Hình vẽ minh họa
Gọi M là trung điểm của BC.
Ta có:
Trong tam giác vuông A’MA có:
Tam giác ABC đều nên
Vậy thể tích khối lăng trụ là:
Cho hai tập hợp A = {a, b, c, d}; B = {c, d, e}. Chọn khẳng định sai trong các khẳng định
sau:
N(A) = 4 => Khẳng định đúng
N(B) = 3 => Khẳng định đúng
A ∩ B = {c, d} => N(A ∩ B) = 2 là khẳng định đúng
A ∪ B = {a, b, c, e} => N(A ∪ B) = 4 => Khẳng định sai là N(A ∪ B) = 7
Cho hai biến cố xung khắc với nhau. Biết xác suất của hai biến cố có giá trị lần lượt là ![]() và
và ![]() . Tính xác suất của biến cố hợp hai biến cố đã cho?
. Tính xác suất của biến cố hợp hai biến cố đã cho?
Gọi hai biến cố là A, B có
Vì hai biến cố A và B là hai biến cố xung khắc nên
Cho hai thùng giấy đựng các viên bi trong đó:
Thùng 1 chứa 4 viên bi trắng, 5 viên bi đỏ và 6 viên bi xanh.
Thùng 2 chứa 7 viên bi trắng, 6 viên bi đỏ và 5 viên bi xanh.
Lấy ngẫu nhiên 1 viên trong mỗi thùng. Gọi A là biến cố “Hai viên bi lấy được cùng màu”. Số kết quả thuận lợi của biến cố A là: 88
Cho hai thùng giấy đựng các viên bi trong đó:
Thùng 1 chứa 4 viên bi trắng, 5 viên bi đỏ và 6 viên bi xanh.
Thùng 2 chứa 7 viên bi trắng, 6 viên bi đỏ và 5 viên bi xanh.
Lấy ngẫu nhiên 1 viên trong mỗi thùng. Gọi A là biến cố “Hai viên bi lấy được cùng màu”. Số kết quả thuận lợi của biến cố A là: 88
Ta có các kết quả thuận lợi cho biến cố A như sau:
Thùng 1 lấy ra 1 viên bi trắng, thùng 2 lấy được 1 viên bi trắng có: cách.
Thùng 1 lấy ra 1 viên bi đỏ, thùng 2 lấy được 1 viên bi đỏ có: cách.
Thùng 1 lấy ra 1 viên bi xanh, thùng 2 lấy được 1 viên bi xanh có: cách.
Suy ra số phần tử của biến cố A là:
Giả sử ![]() thì giá trị của
thì giá trị của ![]() biểu diễn theo
biểu diễn theo ![]() là:
là:
Ta có:
Hai người đi săn cùng bắn vào một con mồi. Gọi A là biến cố người thứ nhất bắn trúng con mồi. B là biến cố người thứ hai bắn trúng con mồi. Mối quan hệ giữa hai biến cố A và B là:
Hai biến cố A và B là hai biến cố độc lập vì việc người thứ nhất bắn trúng con mồi không phụ thuộc vào người thứ hai bắn trúng con mồi.
