Lớp 12 Toán 12

Đề thi HK2 Toán 12 Đề 2

Mô tả thêm: Đề thi HK2 Toán 12 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 50 câu
  • Số điểm tối đa: 50 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng?

    Phương trình chính tắc của đường thẳng có dạng:

    \frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c} với a.b.c eq 0.

    Vậy đáp án đúng là : \frac{x - 6}{3} = \frac{y - 3}{4} = \frac{z - 5}{3}

  • Câu 2: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;4;2),B( - 1;2;4) và đường thẳng \Delta:\left\{ \begin{matrix} x = 1 - t \\ y = - 2 + t \\ z = 2t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight). Điểm M \in \Delta mà tổng MA^{2} + MB^{2} có giá trị nhỏ nhất có tọa độ là:

    Vì M \in \Delta nên ta có tọa độ điểm M(1 - t; - 2 + t;2t).

    Ta có:

    MA^{2} + MB^{2} = ( - t)^{2} + (t - 6)^{2} + (2t - 2)^{2} + (2 - t)^{2} + (t - 4)^{2} + (2t - 4)^{2}

    = 12t^{2} - 48t + 76 = 12(t - 2)^{2} + 28 \geq 28

    Vậy giá trị nhỏ nhất của MA^{2} + MB^{2} là 28 khi t = 2 \Rightarrow M( - 1;0;4).

  • Câu 3: Vận dụng

    Điểm biểu diễn của số phức z = \frac{1}{{2 - 3i}} là:

     Ta có: z = \frac{1}{{2 - 3i}} = \frac{2}{{13}} + \frac{3}{{13}}i

  • Câu 4: Nhận biết

    Trong không gian Oxyz, tìm phương trình mặt phẳng (\alpha) cắt ba trục Ox,Oy,Oz lần lượt tại ba điểm A( - 3;0;0),B(0;4;0),C(0;0; - 2)?

    Phương trình mặt phẳng (\alpha): \frac{x}{- 3} + \frac{y}{4} + \frac{z}{- 2} = 1

    \Leftrightarrow 4x - 3y + 6z = - 12

    \Leftrightarrow 4x - 3y + 6z + 12 = 0

  • Câu 5: Nhận biết

    Tìm nguyên hàm của hàm số f\left( x ight) = 3x + \cos 3x

     Ta có: \int {\left( {3x + \cos 3x} ight)dx = \frac{{3{x^2}}}{2} + \frac{{\sin 3x}}{3} + C}

  • Câu 6: Nhận biết

    Cho số phức z = {\left( {2i} ight)^4} - \frac{{{{\left( {1 + i} ight)}^6}}}{{5i}}. Số phức \overline {5z + 3i} là số phức nào sau đây?

     Ta tính được z = \frac{{88}}{5} \Rightarrow 5z + 3i = 88 + 3i

  • Câu 7: Thông hiểu

    Cho số phức z = a + bi. Số phức {z^2} có phần ảo là:

    Ta có: {z^2} = {\left( {a + bi} ight)^2} = {a^2} - {b^2} + 2abi

  • Câu 8: Vận dụng

    Cho số phức z thoả mãn \frac{1+i}{z} là số thực và |z-2|=m với m∈\mathbb{R}. Gọi m_0 là một giá trị của m để có đúng một số phức thoả mãn bài toán. Khi đó:

    Giả sử z=a+bi,(a,b∈ \mathbb R)..

    Đặt: w=\frac{1+i}{z}=\frac{1+i}{a+bi}

    =\frac{1}{a^2+b^2}[a+b+(a-b)i]=\frac{a+b}{a^2+b^2 }+\frac{a-b}{a^2+b^2 } i.

    w là số thực nên: a=b(1).

    Mặt khác:  |a-2+bi|=m⇔(a-2)^2+b^2=m^2

    Thay (1) vào (2) được: (a-2)^2+a^2=m^2⇔2a^2-4a+4-m^2=0

    Để có đúng một số phức thoả mãn bài toán thì PT (3) phải có nghiệm duy nhất a. \Leftrightarrow \Delta '=0 \Leftrightarrow 4-2(4-m^2 )=0 \Leftrightarrow m^2=2 \Leftrightarrow m= \sqrt 2 \in (1;\frac {3}{2})

    (Vì m là mô-đun).

  • Câu 9: Vận dụng

    Cho số phức z = {\left( {\frac{{4i}}{{i + 1}}} ight)^m}, m nguyên dương. Có bao nhiêu giá trị m \in \left[ {1;100} ight] để z là số thực?

    Ta có: z = {\left( {\frac{{4i}}{{i + 1}}} ight)^m} = {(8i)^{\frac{m}{2}}} = {8^{\frac{m}{2}}}.{i^{\frac{m}{2}}}

    z là số thực khi và chỉ khi \frac{m}{2} = 2k \Leftrightarrow m = 4k,\,\,k \in \mathbb N

    Vậy có 25 giá trị m thỏa yêu cầu đề bài.

  • Câu 10: Thông hiểu

    Trong không gian với hệ trục tọa độ Oxyz, cho  A(1;2; - 1);\overrightarrow{AB} =(1;3;1), khi đó tọa độ điểm B là:

    Gọi B(x;y;z) ta có:

    A(1;2; - 1);\overrightarrow{AB} =(1;3;1) khi đó \left\{\begin{matrix}x - 1 = 1 \\y - 2 = 3 \\z + 1 = 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x = 2 \\y = 5 \\z = 0 \\\end{matrix} ight. nên tọa độ điểm cần tìm là B(2;5;0).

  • Câu 11: Nhận biết

    Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (\alpha):x + y + z - 6 = 0. Điểm nào dưới đây không thuộc mặt phẳng (\alpha)?

    Điểm M(1; - 1;1) không thuộc mặt phẳng (\alpha):x + y + z - 6 = 0.

  • Câu 12: Vận dụng cao

    Tích phân I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\frac{{\cos x - \sin x}}{{\left( {{e^x}\cos x + 1} ight)\cos x}}dx} có giá trị là:

    Ta biến đổi: I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\frac{{{e^x}.\left( {\cos x - \sin x} ight)}}{{\left( {{e^x}\cos x + 1} ight){e^x}\cos x}}dx}

    Đặt t = {e^x}\cos x \Rightarrow dt = {e^x}\left( {\cos x - \sin x} ight)dx

    Đổi cận \left\{ \begin{gathered} x = \frac{\pi }{3} \Rightarrow t = \frac{1}{2}{e^{\frac{\pi }{3}}} \hfill \\ x = \frac{{2\pi }}{3} \Rightarrow t = - \frac{1}{2}{e^{\frac{{2\pi }}{3}}} \hfill \\ \end{gathered} ight.

    I = \int\limits_{\frac{1}{2}{e^{\frac{\pi }{3}}}}^{ - \frac{1}{2}{e^{\frac{{2\pi }}{3}}}} {\frac{1}{{t\left( {t + 1} ight)}}dt} = \left. {\left( {\ln \left| {\frac{t}{{t + 1}}} ight|} ight)} ight|_{\frac{1}{2}{e^{\frac{\pi }{3}}}}^{ - \frac{1}{2}{e^{\frac{{2\pi }}{3}}}}

    = \ln \left| {\frac{{{e^{\frac{{2\pi }}{3}}}}}{{{e^{\frac{{2\pi }}{3}}} - 2}}} ight| - \ln \left| {\frac{{{e^{\frac{\pi }{3}}}}}{{{e^{\frac{\pi }{3}}} + 2}}} ight| = \ln \left| {\frac{{{e^{\frac{\pi }{3}}}\left( {{e^{\frac{\pi }{3}}} + 2} ight)}}{{{e^{\frac{{2\pi }}{3}}} - 2}}} ight|

  • Câu 13: Nhận biết

    Tìm nguyên hàm của hàm số f(x) = e^{x}\left( 2017 - \frac{2018e^{- x}}{x^{5}} ight)?

    Ta có: \int_{}^{}\left\lbrack e^{x}\left( 2017 - \frac{2018e^{- x}}{x^{5}} ight) ightbrack dx = \int_{}^{}\left( 2017e^{x} - \frac{2018}{x^{5}} ight)dx

    = 2017e^{x} + \frac{504,5}{x^{4}} + C

  • Câu 14: Vận dụng

    Trong không gian Oxyz, cho điểm I(1; 1; 1). Phương trình mặt phẳng (P) cắt trục Ox, Oy, Oz lần lượt tại A, B, C (không trùng với gốc tọa độ O) sao cho I là tâm đường tròn ngoại tiếp tam giác ABC?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong không gian Oxyz, cho điểm I(1; 1; 1). Phương trình mặt phẳng (P) cắt trục Ox, Oy, Oz lần lượt tại A, B, C (không trùng với gốc tọa độ O) sao cho I là tâm đường tròn ngoại tiếp tam giác ABC?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 15: Thông hiểu

    Cho F(x) là một nguyên hàm của hàm số f\left( x ight) = {e^x} + 2x thỏa mãn F\left( 0 ight) = \frac{3}{2}. Tìm F(x).

     F\left( x ight) = \int {f\left( x ight)dx = \int {\left( {{e^x} + 2x} ight)dx = {e^x} + {x^2} + C} }

    Theo bài ra ta có:

    F\left( 0 ight) = \frac{3}{2} \Rightarrow {e^x} + {x^2} + C = \frac{3}{2} \Rightarrow C = \frac{1}{2}

    => F\left( x ight) = {e^x} + {x^2} + \frac{1}{2}

  • Câu 16: Thông hiểu

    Hàm số F(x) là một nguyên hàm của hàm số y = \frac{1}{x} trên ( - \infty;0) thỏa mãn F( - 2) = 0. Khẳng định nào sau đây đúng?

    Ta có: F(x) = \int_{}^{}{\frac{1}{x}dx} = \ln|x| + C = \ln( - x) + C;\forall x \in ( - \infty;0)

    Lại có F( - 2) = 0 \Leftrightarrow \ln(2) + C = 0 \Rightarrow C = - ln2

    Do đó F(x) = \ln( - x) - ln2 = \ln\left( - \frac{x}{2} ight)

    Vậy F(x) = \ln\left( - \frac{x}{2} ight);\forall x \in ( - \infty;0).

  • Câu 17: Thông hiểu

    Phần thực của số phức z = 5 + 2i - {\left( {1 + i} ight)^3} là:

    Ta có:

    z = 5 + 2i - {\left( {1 + i} ight)^3} = 5 + 2i + 2 - 2i = 7

  • Câu 18: Nhận biết

    Cho hình phẳng (H) giới hạn bởi các đường y = 2x - x^{2};y = 0. Quay (H) quanh trục hoành tạo thành khối tròn xoay có thể tích là:

    Ta có: 2x - x^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.

    Theo công thức thể tích giới hạn bởi các đường ta có:

    V = \pi\int_{0}^{2}{\left( 2x - x^{2} ight)^{2}dx}

  • Câu 19: Thông hiểu

    Cho số phức z = 1 + \left( {1 + i} ight) + {\left( {1 + i} ight)^2} + ... + {\left( {1 + i} ight)^{26}}. Phần thực của số phức z là?

     Ta có: z = 1 + \left( {1 + i} ight) + {\left( {1 + i} ight)^2} + ... + {\left( {1 + i} ight)^{26}} = \frac{{{{\left( {1 + i} ight)}^{27}} - 1}}{i}

    = \frac{{{{\left( {1 + i} ight)}^{26}}.\left( {1 + i} ight) - 1}}{i} = \frac{{{{(2i)}^{13}}\left( {1 + i} ight) - 1}}{i}

    = \frac{{{2^{13}}i - {2^{13}} - 1}}{i} = {2^{13}} + (1 + {2^{13}})i

    Vậy phần thực là  2^{13}.

  • Câu 20: Thông hiểu

    Tính diện tích S_{D} của hình phẳng D được giới hạn bởi các đường y = \left| \frac{\ln x}{x} ight|, trục hoành và các đường thẳng x = \frac{1}{e};x = 2?

    Diện tích hình phẳng cần tìm là:

    S_{D} = \int_{\frac{1}{e}}^{2}{\left| \frac{\ln x}{x} ight|dx} = \int_{\frac{1}{e}}^{1}{\left| \frac{\ln x}{x} ight|dx} + \int_{1}^{2}{\left| \frac{\ln x}{x} ight|dx}

    = - \int_{\frac{1}{e}}^{1}{\frac{\ln x}{x}dx} + \int_{1}^{2}{\frac{\ln x}{x}dx}

    = - \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{\frac{1}{e}}^{1} + \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{1}^{2}

    = \frac{1}{2} + \frac{\ln^{2}2}{2} =\frac{1}{2}\left( 1 + \ln^{2}2 ight)

  • Câu 21: Nhận biết

    Số phức liên hợp của số phức 5 - 3i là

    \overline z = \overline {a + bi} = a – bi

    \Rightarrow \overline z = \overline {5 - 3i} = 5 - ( - 3i) = 5 + 3i

  • Câu 22: Thông hiểu

    Số phức z = \frac{{3 - 4i}}{{4 - i}} bằng:

     Ta có: z = \frac{{3 - 4i}}{{4 - i}} = \frac{{16}}{{17}} - \frac{{13}}{{17}}i

  • Câu 23: Vận dụng

    Xét phương trình {z^3} = 1 trên tập số phức. Tập nghiệm của phương trình là:

     Ta có:

    {z^3} = 1 \Leftrightarrow \left( {z - 1} ight)\left( {{z^2} + z + 1} ight) = 0

    \Leftrightarrow \left[ \begin{array}{l}z = 1\\{z^2} + z + 1 = 0\end{array} ight. \Leftrightarrow \left[ \begin{array}{l}z = 1\\z = - \frac{1}{2} \pm \frac{{\sqrt 3 }}{2}i\end{array} ight.

    Suy ra: S = \left\{ {1; - \frac{1}{2} \pm \frac{{\sqrt 3 }}{2}i} ight\}

  • Câu 24: Thông hiểu

    Trong không gian hệ trục tọa độ Oxyz, cho các vectơ \overrightarrow{a} = (2;3;1),\overrightarrow{b} = ( - 1;5;2),\overrightarrow{c} = (4; - 1;3),\overrightarrow{x} = ( - 3;22;5). Đẳng thức nào dưới đây đúng?

    Đặt \overrightarrow{x} = m\overrightarrow{a} + n\overrightarrow{b} + p\overrightarrow{c};\left( m;n;p\mathbb{\in R} ight)

    \Rightarrow ( - 3;22;5) = m(2;3;1) + n( - 1;5;2) + p(4; - 1;3)

    \Rightarrow \left\{ \begin{matrix} 2m - m + 4p = - 3 \\ 3m + 5m - p = 22 \\ m + 2m + 3p = 5 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} m = 2 \\ n = 3 \\ p = - 1 \\ \end{matrix} ight.

    Vậy \overrightarrow{x} = 2\overrightarrow{a} + 3\overrightarrow{b} - \overrightarrow{c} là đẳng thức đúng.

  • Câu 25: Thông hiểu

    Tìm tất cả các giá trị thực của tham số m để tồn tại tích phân \int_{1}^{1 + m}\frac{dx}{x(x - 5)(x - 4)}?

    Tích phân \int_{1}^{1 + m}\frac{dx}{x(x - 5)(x - 4)} tồn tại khi và chỉ khi hàm số y = \frac{1}{x(x - 5)(x - 4)} liên tục trên \lbrack 1;1 + mbrack hoặc \lbrack 1 + m;1brack

    Mà hàm số y = \frac{1}{x(x - 5)(x - 4)} liên tục trên các khoảng ( - \infty;0),(0;4),(4;5),(5; + \infty)

    Nên hàm số y = \frac{1}{x(x - 5)(x - 4)} liên tục trên \lbrack 1;1 + mbrack hoặc \lbrack 1 + m;1brack khi và chỉ khi

    0 < 1 + m < 4 \Leftrightarrow - 1 < m < 3 \Rightarrow m \in ( - 1;3).

  • Câu 26: Nhận biết

    Số phức có phần thực bằng 3 và phần ảo bằng 4 là

     Số phức z = a + bi có a được gọi là phần ảo, b là phần thực.

  • Câu 27: Nhận biết

    Phương trình sau có tập nghiệm trên trường số phức là: z^4 + 2z^2 -3 = 0

     Ta có  z^4 + 2z^2 -3 = 0

    \Leftrightarrow \left[ \begin{array}{l}{z^2} = 1\\{z^2} = - 3\end{array} ight. \Leftrightarrow \left[ \begin{array}{l}z = \pm 1\\z = \pm i\sqrt 3 \end{array} ight.

    Vậy phương trình có 4 nghiệm: \left[ \begin{array}{l}z = \pm 1\\z = \pm i\sqrt 3 \end{array} ight.

  • Câu 28: Vận dụng

    Cho số phức z thỏa mãn \left| {z - 1 + i} ight| = 2. Chọn phát biểu đúng:

     Giả sử: z = x + yi{\text{ }}\left( {x,y \in \mathbb{R}} ight)

    Theo bài ra ta có:

    \left| {z - 1 + i} ight| = 2

    \Leftrightarrow \left| {\left( {x - 1} ight) + \left( {y + 1} ight)i} ight| = 2

    \Leftrightarrow {\left( {x - 1} ight)^2} + {\left( {y + 1} ight)^2} = 4

  • Câu 29: Nhận biết

    Cho số phức {z_1} = 1 + 2i và {z_2} = - 1 - 2i. Khẳng định nào sau đây là khẳng định đúng?

     Ta có: {z_1}.{z_2} = - {\left( {1 + 2i} ight)^2} = - \left( {1 + 4i - 4} ight) = 3 - 4i

    Vậy {z_1}.{z_2} = 3 - 4i là khẳng định đúng.

  • Câu 30: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - 3y + z - 6 = 0 cắt ba trục tọa độ Ox,Oy,Oz lần lượt tại ba điểm A,B,C. Lúc đó thể tích V của khối tứ diện OABC là:

    Gọi A(a;0;0),B(0;b;0),C(0;0;c) lần lượt là giao của mặt phẳng (P) với ba trục tọa độ Ox,Oy,Oz.

    Khi đó A(3;0;0),B(0; - 2;0),C(0;0;6) và tứ diện OABC có OA,OB,OC đôi một vuông góc tại O.

    Do đó V_{OABC} = \frac{1}{6}OA.OB.OC = \frac{1}{6}.3.2.6 = 6

  • Câu 31: Thông hiểu

    Gọi F(x) là một nguyên hàm của hàm số f\left( x ight) = \cos 5x.\cos x thỏa mãn F\left( {\frac{\pi }{5}} ight) = 0. Tính F\left( {\frac{\pi }{6}} ight).

     \begin{matrix} \cos 5x + \cos x = \dfrac{1}{2}\left( {\cos 6x + \cos 4x} ight) \hfill \\ \int {\cos 5x.\cos xdx} = \int {\dfrac{1}{2}\left( {\cos 6x + \cos 4x} ight)} dx = \dfrac{1}{2}.\dfrac{{\sin 6x}}{6} + \dfrac{1}{2}\dfrac{{\sin 4x}}{4} + C \hfill \\ F\left( {\dfrac{\pi }{3}} ight) = 0 \Rightarrow C = \dfrac{{\sqrt 3 }}{6} \hfill \\ F\left( {\dfrac{\pi }{6}} ight) = \dfrac{{\sqrt 3 }}{8} \hfill \\ \end{matrix}

  • Câu 32: Vận dụng

    Gọi {z_1},{z_2},{z_3},{z_4} là bốn nghiệm phức của phương trình 2{z^4} - 3{z^2} - 2 = 0. Tổng T = \left| {{z_1}} ight| + \left| {{z_2}} ight| + \left| {{z_3}} ight| + \left| {{z_4}} ight|  bằng:

     Ta có:  2{z^4} - 3{z^2} - 2 = 0 \Leftrightarrow \left( {2{z^2} + 1} ight)\left( {{z^2} - 2} ight) = 0

    \Leftrightarrow \left( {z + \frac{{\sqrt 2 }}{2}i} ight)\left( {z - \frac{{\sqrt 2 }}{2}i} ight)\left( {z - \sqrt 2 } ight)\left( {z + \sqrt 2 } ight) = 0

    \Leftrightarrow \left[ \begin{array}{l}{z_1} = - \dfrac{{\sqrt 2 }}{2}i\\{z_2} = \dfrac{{\sqrt 2 }}{2}i\\{z_3} = \sqrt 2 \\{z_4} = - \sqrt 2 \end{array} ight.

    T = \left| {{z_1}} ight| + \left| {{z_2}} ight| + \left| {{z_3}} ight| + \left| {{z_4}} ight| = 3\sqrt 2

  • Câu 33: Nhận biết

    Họ nguyên hàm của hàm số f(x) =2\sin x.\cos2x là:

    Ta có: f(x) = 2\sin x.\cos2x = \sin( - x) +\sin3x = - \sin x + \sin3x

    Khi đó:

    \int_{}^{}{f(x)dx} = \int_{}^{}{\left( -\sin x + \sin3x ight)dx}

    = \int_{}^{}{\left( - \sin x ight)dx}+ \int_{}^{}{(\sin3x)dx} = \cos x - \frac{1}{3}\cos3x + C

  • Câu 34: Vận dụng cao

    Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2;2;0), B(1;0;-2) và mặt

    phẳng(P): x+2y-z-1=0. Gọi M(a;b;c) là điểm thuộc mặt phẳng (P) sao cho MA=MB

    và góc \widehat{ABM} có số đo lớn nhất. Khi đó giá trị a+4b+c bằng ?

    MA=MB nên M thuộc mặt phẳng mặt phẳng trung trực của đoạn thẳng AB. Ta có phương trình trung trực của AB là (Q); y+z=0

     M thuộc giao tuyến của hai mặt phẳng (P) và (Q) nên M thuộc đường thẳng

    (d): \left\{\begin{matrix} x=1+3t \\ y=-t \\ z=t \end{matrix}ight..

    Gọi M( 1+3t;-t;t) , ta có \cos\widehat{AMB}=\dfrac{\left | \vec{MA}.\vec{MB} ight | }{MA.MB}=\dfrac{11t^2-2t+1}{11t^2-2t+5}.

    Khảo sát hàm số f(t)=\dfrac{11t^2-2t+1}{11t^2-2t+5} , ta được f(t)=\frac{5}{27} khi t=\frac{1}{11} .

    Suy ra \widehat{AMB}  có số đo lớn nhất khi t=\frac{1}{11} , ta có M(\frac{14}{11}; \frac{-1}{11};\frac{1}{11}).

    Khi đó giá trị a+4b+c=1.

  • Câu 35: Vận dụng

    Cho hàm số y = f(x) thỏa mãn f'(x).f^{2}(x) = x^{2} và f(2) = 2. Phương trình tiếp tuyến của đồ thị hàm số g(x) = f(x) + x^{2} tại điểm có hoành độ bằng 3 là:

    Ta có: f'(x).f^{2}(x) = x^{2}

    Lấy nguyên hàm hai vế ta được:

    \int_{}^{}{f'(x).f^{2}(x)dx} = \int_{}^{}{x^{2}dx}

    \Leftrightarrow \int_{}^{}{f^{2}(x)df(x)} = \frac{x^{3}}{3} + C

    \Leftrightarrow \frac{f^{3}(x)}{3} = \frac{x^{3}}{3} + C. Theo bài ra ta có: f(2) = 2 \Rightarrow \frac{f^{3}(2)}{3} = \frac{2^{3}}{3} + C \Rightarrow C = 0

    Suy ra \frac{f^{3}(x)}{3} = \frac{x^{3}}{3} \Leftrightarrow f(x) = x

    Vậy g(x) = x^{2} + x \Rightarrow g'(x) = 2x + 1

    Ta có: g'(3) = 7;g(3) = 12

    Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng 3 là:

    y = g'(3)(x - 3) + g(3)

    \Leftrightarrow y = 7(x - 3) + 12 \Leftrightarrow y = 7x - 9

  • Câu 36: Nhận biết

    Tích phân I = \int\limits_0^{\dfrac{\pi }{2}} {\sin xdx} có giá trị là:

    Tích phân I = \int\limits_0^{\dfrac{\pi }{2}} {\sin xdx} có giá trị là:

    I = \int\limits_0^{\dfrac{\pi }{2}} {\sin xdx} = \left. {\left( { - \cos x} ight)} ight|_0^{\dfrac{\pi }{2}} = 1

    Ngoài ra ta có thể sử dụng máy tính cầm tay nhập trực tiếp biểu thức và tính ra kết quả.

  • Câu 37: Vận dụng cao

    Cho hàm số f(x) liên tục trên đoạn \lbrack - 6;5brack có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ:

    Tính giá trị I = \int_{- 6}^{5}{\left\lbrack f(x) + 2 ightbrack dx}?

    Hình vẽ minh họa

    Dựa vào đồ thị ta có: A( - 6; - 1),B( - 2;1) suy ra phương trình đường thẳng AB:y = \frac{1}{2}x + 2

    \Rightarrow I_{1} = \int_{0}^{- 2}{\left\lbrack \frac{1}{2}x + 2 + 2 ightbrack dx} = 8

    Phương trình đường tròn (C): x^{2} + (y - 1)^{2} = 4 \Rightarrow y = 1 + \sqrt{4 - x^{2}}

    \Rightarrow I_{2} = \int_{- 2}^{2}{\left\lbrack 1 + \sqrt{4 - x^{2}} + 2 ightbrack dx} = 12 + 2\pi

    Điểm C(2;1),D(5;3) nên phương trình đường thẳng CD là: y = \frac{2}{3}x - \frac{1}{3}

    \Rightarrow I_{3} = \int_{2}^{5}{\left\lbrack \frac{2}{3}x - \frac{1}{3} + 2 ightbrack dx} = 12

    Vậy I = I_{1} + I_{2} + I_{3} = 32 + 2\pi

  • Câu 38: Nhận biết

    Giả sử f(x) là một hàm số bất kì và liên tục trên khoảng (\alpha;\beta) và a;b;c;b + c \in (\alpha;\beta). Mệnh đề nào sau đây sai?

    Dựa vào tính chất của tích phân với f(x) là một số bất kì liên tục trên khoảng (\alpha;\beta) và a;b;c;b + c \in (\alpha;\beta) ta có:

    \int_{a}^{b}{f(x)dx} = \int_{a}^{c}{f(x)dx} + \int_{c}^{b}{f(x)dx}

    = \int_{a}^{c}{f(x)dx} - \int_{b}^{c}{f(x)dx}

    = \int_{a}^{b + c}{f(x)dx} + \int_{b + c}^{b}{f(x)dx}

  • Câu 39: Nhận biết

    Cho số phức z = a + bi,\left( {a,b \in \mathbb{R}} ight) thỏa mãn \left( {1 + i} ight)z + 2\overline z = 3 + 2i. Tính P = a + b

    Giả sử: z = a + bi{\text{ }}\left( {a,b \in \mathbb{R}} ight)

    \left( {1 + i} ight)\left( {a + bi} ight) + 2\left( {a - bi} ight) = 3 + 2i

    \Leftrightarrow 3a - b + \left( {a - b} ight)i = 3 + 2i

    \Leftrightarrow \left\{ \begin{gathered} 3a - b = 3 \hfill \\ a - b = 2 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} a = \frac{1}{2} \hfill \\ b = - \frac{3}{2} \hfill \\ \end{gathered} ight.

    \Rightarrow P = a + b = - 1

  • Câu 40: Thông hiểu

    Tìm một nguyên hàm F(x) của hàm số f(x) = x.e^{- x} thỏa mãn F(0) = 1?

    Ta có: \left\{ \begin{matrix} u = x \\ dv = e^{- x}dx \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} du = dx \\ v = - e^{- x} \\ \end{matrix} ight.

    \int_{}^{}{f(x)dx} = \int_{}^{}{\left( x.e^{- x} ight)dx}

    = - xe^{- x} + \int_{}^{}{e^{- x}dx} + C

    = - xe^{- x} - e^{- x} + C. Theo bài ra ta có: F(0) = 1 \Leftrightarrow - 1 - 1 + C = 1 \Rightarrow C = 2

    Vậy - (x + 1)e^{- x} + 2 là đáp án cần tìm.

  • Câu 41: Thông hiểu

    Tính tổng tất cả các nghiệm của phương trình sau: (z^2 + z)^2 + 4(z^2 + z) -12 = 0 là?

     Đặt t = z^2 + z, khi đó phương trình đã cho có dạng:

    t^2 + 4t – 12 = 0 \Leftrightarrow\left[ \begin{array}{l}t = - 6\\t = 2\end{array} ight.

    \Leftrightarrow \left[ \begin{array}{l}{z^2} + z - 6 = 0\\{z^2} + z - 2 = 0\end{array} ight.

    \Leftrightarrow \left[ \begin{array}{l}z = \dfrac{{ - 1 + \sqrt {23} i}}{2}\\z = \dfrac{{ - 1 - \sqrt {23} i}}{2}\\z = 1\\z = - 2\end{array} ight.

    Vậy phương trình đã cho có 4 nghiệm có tổng là

    \frac{{ - 1 + \sqrt {23} i}}{2} + \frac{{ - 1 - \sqrt {23} i}}{2} + 1 - 2 = - 1 + 1 - 2 = - 2

  • Câu 42: Thông hiểu

    Cho hai số phức {z_1} = 1 - i;{z_2} = 3 + 2i. Phần thực và phần ảo của số phức {z_1},{z_2} tương ứng bằng:

     Ta có: {z_1}.{z_2} = \left( {1 - i} ight)\left( {3 + 2i} ight) = 5 - i

  • Câu 43: Nhận biết

    Hàm số f(x) = x^{3} + \sin x là một nguyên hàm của hàm số nào sau đây?

    Ta có: F'(x) = 3x^{2} + \cos x

  • Câu 44: Nhận biết

    Trong \mathbb C, phương trình 2x^2+x+1=0 có nghiệm là:

     Ta có: \Delta = {b^2} - 4ac = {1^2} - 4.2.1 = - 7 = 7{i^2} < 0 nên phương trình có hai nghiệm phức là: {x_{1,2}} = \frac{{ - 1 \pm i\sqrt 7 }}{4}

  • Câu 45: Thông hiểu

    Cho phương trình sau: z^4 – 4z^3 +7z^2 – 16z + 12 = 0. Tính tổng số tất cả các nghiệm của phương trình?

    4 || Bốn || bốn

    Đáp án là:

    Cho phương trình sau: z^4 – 4z^3 +7z^2 – 16z + 12 = 0. Tính tổng số tất cả các nghiệm của phương trình?

    4 || Bốn || bốn

    Do tổng tất cả các hệ số của phương trình z^4 – 4z^3 +7z^2 – 16z + 12 = 0 bằng 0 nên z^4 – 4z^3 +7z^2 – 16z + 12 = 0 có nghiệm z = 1.

    z^4 – 4z^3 +7z^2 – 16z + 12 = 0\Leftrightarrow (z – 1)(z^3 – 3z^2 + 4z – 12) = 0

    \Leftrightarrow (z – 1) (z – 3) (z^2 + 4) = 0

    \Leftrightarrow\left[ \begin{array}{l}z = 1\\z = 3\\{z^2} + 4 = 0\end{array} ight. \Leftrightarrow \left[ \begin{array}{l}z = 1\\z = 3\\z = 2i\\z = - 2i\end{array} ight.

    Vậy phương trình đã cho có 4 nghiệm và cộng tổng chúng lại ta được 4.

  • Câu 46: Nhận biết

    Cho số phức z = 1 - i + {i^3}. Tìm phần thực a và phần ảo b của z.

     Ta có z = 1 - i + {i^3} = 1 - i - i = 1 - 2i \Rightarrow a = 1,b = - 2

  • Câu 47: Vận dụng

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash\left\{ 0 ight\} thỏa mãn f(x) + xf'(x) = 3x^{2} và f(2) = 8. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại giao điểm với trục hoành là:

    Ta có: f(x) + xf'(x) = 3x^{2}

    \Leftrightarrow (x)'f(x) + xf'(x) = 3x^{2}

    \Leftrightarrow \left( xf'(x) ight)' = 3x^{2}

    Lấy nguyên hàm hai vế ta được:

    \int_{}^{}{\left( xf'(x) ight)'dx} = \int_{}^{}{3x^{2}dx} \Leftrightarrow xf(x) = x^{3} + C

    Lại có f(2) = 8 \Rightarrow 2f(2) = 8 + C \Leftrightarrow 2.8 = C + 8 \Leftrightarrow C = 8

    Từ đó suy ra xf(x) = x^{3} + 8 \Leftrightarrow f(x) = \frac{x^{3} + 8}{x}

    Xét phương trình hoành độ giao điểm \frac{x^{3} + 8}{x} = 0 \Leftrightarrow x = - 2

    Ta có: f'(x) = \frac{2x^{3} - 8}{x^{2}} \Rightarrow f'( - 2) = - 6;f( - 2) = 0

    Phương trình tiếp tuyến tại giao điểm với trục hoành là

    y = f'( - 2)(x + 2) + f( - 2)

    \Leftrightarrow y = - 6(x + 2) \Rightarrow y = - 6x - 12

  • Câu 48: Nhận biết

    Cho hình chóp S.ABC có đường thẳng SA vuông góc với đáy (ABC), SA = 2a. Khoảng cách từ điểm S đến đường thẳng AB bằng:

    Vì SA vuông góc với đáy (ABC) nên SA\bot AB \Rightarrow d(S,AB) = SA = 2a

  • Câu 49: Thông hiểu

    Tính thể tích V của khối lập phương ABCD.A'B'C'D', biết AC' = a\sqrt 3.

     

    Đặt cạnh của khối lập phương là x  ( x > 0)

    Suy ra CC' = x;\,{\text{ }}AC = x\sqrt 2.

    Tam giác vuông ACC', có

    AC' = \sqrt {A{C^2} + CC{'^2}} \Leftrightarrow x\sqrt 3 = a\sqrt 3 \Rightarrow x = a

    Vậy thể tích khối lập phương V = a^3.

  • Câu 50: Vận dụng cao

    Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(3; 2; 1), C\left( - \frac{5}{3};\frac{4}{3};\frac{8}{3} ight) và M thay đổi sao cho hình chiếu của M lên mặt phẳng (ABC) nằm trong tam giác ABC và các mặt phẳng (MAB),(MBC),(MCA) hợp với mặt phẳng (ABC) các góc bằng nhau. Tính giá trị nhỏ nhất của OM.

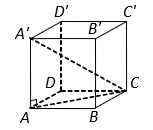
    Hình vẽ minh họa

    Gọi H là hình chiếu của M lên mặt phẳng (ABC).

    Giả thiết suy ra H là tâm đường tròn nội tiếp tam giác ABC nên thỏa mãn

    BC.\overrightarrow{HA} + AC.\overrightarrow{HB} + AB.\overrightarrow{HC} = \overrightarrow{0}

    Ta có AB = 3, AC = 4, BC = 5, suy ra

    \left\{ \begin{matrix} 5(x - 1) + 4(x - 3) + 3x + 5 = 0 \\ 5y + 4(y - 2) + 3y - 4 = 0\ \\ 5z + 4(z - 1) + 3z - 8 = 0\ \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 1 \\ y = 1 \\ z = 1 \\ \end{matrix} ight.\ \Rightarrow H(1;1;1)

    Phương trình đường thẳng MH nhận \overrightarrow{u} = \overrightarrow{n_{ABC}} làm vectơ chỉ phương nên MH là: \left\{ \begin{matrix} x\ = \ 1\ + \ t \\ y\ = \ 1\ - \ 2t \\ z\ = \ 1\ + \ 2t \\ \end{matrix} ight.

    Khi đó: OM_{\min} = \frac{\left| \left\lbrack \overrightarrow{MH};\overrightarrow{OH} ightbrack ight|}{\left| \overrightarrow{MH} ight|} = \frac{\sqrt{26}}{3}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi HK2 Toán 12 Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 66 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi HK2 Toán 12 Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/50
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập