Lớp 10 Toán 10 - Cánh diều

Đề thi học kì 1 Toán 10 Cánh Diều Đề 1

Mô tả thêm: Đề thi học kì 1 Toán 10 được biên soạn gồm 45 câu hỏi bám sát 4 chuyên đề giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức môn Toán lớp 10 sách Cánh Diều.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho hàm số y = f(x) có đồ thị như hình vẽ. Hãy so sánh f(2017) với số 0.

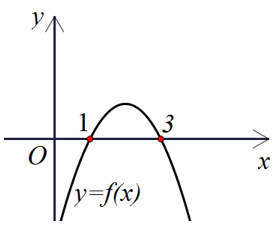
    Nhìn đồ thị, ta thấy đồ thị y = f(x) cắt trục hoành tại 2 điểm x = 1, x = 3 nên Δ > 0, dựa vào hình dạng parabol nên suy ra a < 0 và ta có bảng xét dấu như sau:

    Dựa vào bảng xét dấu thì f(x) < 0 khi x < 1 ∨ x > 3. Mà 2017 > 3 nên f(2017) < 0.

  • Câu 2: Nhận biết

    Cho A = {a, b}. Số tập con của A là:

     Ta có: Số tập hợp con của tập có n phần tử là 2^n. Do đó số tập con của A là 2^2=4.

  • Câu 3: Vận dụng cao

    Phương trình x^{2} = \sqrt{2 - x} + 2 có mấy nghiệm nguyên ?

    Đặt t = \sqrt{2 - x}\ \ \ (t \geq 0). Ta có hệ phương trình:

    \left\{ \begin{matrix} x^{2} = t + 2 \\ t^{2} = - x + 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} t = - x \\ t = x - 1 \\ \end{matrix} ight.

    Với t =  − x ta được \left\lbrack \begin{matrix} x = 1 \Rightarrow t = - 1(L) \\ x = - 2 \Rightarrow t = 2(TM) \\ \end{matrix} ight.

    Với t = x − 1 ta được \left\lbrack \begin{matrix} x = \frac{1 + \sqrt{5}}{2} \Rightarrow t = \frac{\sqrt{5} - 1}{2}(TM) \\ x = \frac{1 - \sqrt{5}}{2} \Rightarrow t = \frac{- \sqrt{5} - 1}{2}(L) \\ \end{matrix} ight.

    Vậy phương trình có 2 nghiệm x =  − 2 và x = \frac{1 + \sqrt{5}}{2}.

  • Câu 4: Thông hiểu

    Cho tam thức f(x) = ax^{2} + bx + c (a ≠ 0), có ∆ = b^{2} – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:

    Biểu thức f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:

    \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a < 0} \\ {\Delta ' \leqslant 0} \end{array}} ight.

  • Câu 5: Thông hiểu

    Cho 2 mệnh đề: “Quyển vở này của Nam” và “Quyển vở này có 118 trang”.

    Cho biết 2 mệnh đề trên đều đúng, tìm mệnh đề sai trong các mệnh đề sau:

    Đặt P: “Quyển vở này của Nam”, Q: “Quyển vở này có 118 trang”

    Theo đề bài, P đúng, Q đúng nên \overline{P} sai, \overline{Q} sai.

    Mệnh đề P \Rightarrow Q chỉ sai khi P đúng Q sai.

    Chọn đáp án Quyển vở này của Nam nên nó không có 118 trang.

  • Câu 6: Thông hiểu

    Cặp nghiệm nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: x + 2y - 1 < 0?

    (x; y) = (2; 3) => x = 2;{\text{ }}y = 3 thay vào bất phương trình ta có:

    2 + 2.3 - 1 = 7 > 0 => Đáp án sai

    (x; y) = (1; 2) => x = 1;{\text{ }}y = 2 thay vào bất phương trình ta có:

    1 + 2.2 - 1 = 4 > 0 => Đáp án sai

    (x; y) = (0; 1) => x = 0;{\text{ }}y = 1 thay vào bất phương trình ta có:

    0 + 2.1 - 1 = 1> 0 => Đáp án sai

    (x; y) = (-1; 0) => x = -1;{\text{ }}y = 0 thay vào bất phương trình ta có:

    -1 + 2.0 - 1 = -2 < 0 => Đáp án đúng

    Vậy (x; y) = (-1; 0) là nghiệm của bất phương trình bậc nhất hai ẩn: x + 2y - 1 < 0

  • Câu 7: Thông hiểu

    Cho hai lực \overrightarrow{F_1} và \overrightarrow{F_2} có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực \overrightarrow{F_1} và \overrightarrow{F_2} lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là:

     

    Ta có: \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } ight| = \sqrt {{{80}^2} + {{60}^2}} = 100N.

  • Câu 8: Thông hiểu

    Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng (\overrightarrow{OA}+\overrightarrow{OB})\overrightarrow{AB}=0 là:

     Chọn đáp án: Tam giác OAB cân tại O.

    Gọi M là trung điểm AB.

    Ta có: \left( {\overrightarrow {OA} + \overrightarrow {OB} } ight).\overrightarrow {AB} = 2\overrightarrow {OM} .\overrightarrow {AB} = 0 (do OM\perp AB).

  • Câu 9: Nhận biết

    Cặp số (2;3) là nghiệm của bất phương trình nào sau đây?

    Vì 2 - 3 < 0 là mệnh đề đúng nên cặp số (2;3) là nghiệm của bất phương trình x–y < 0.

  • Câu 10: Thông hiểu

    Trong các mệnh đề sau, mệnh đề nào là sai:

    Ta thấy mệnh đề A ∈ A sai vì giữa hai tập hợp không có quan hệ phụ thuộc.

  • Câu 11: Vận dụng cao

    Cho tam giác ABC. Lấy các điểm M,N sao cho \overrightarrow{MA} + \overrightarrow{MB} = \overrightarrow{0};2\overrightarrow{NA} + 3\overrightarrow{NC} = \overrightarrow{0} và \overrightarrow{BC} = k\overrightarrow{BP}. Xác định k để ba điểm M,N,P thẳng hàng.

    Ta có:

    \overrightarrow{MN} = \overrightarrow{AN} - \overrightarrow{AM} = \frac{3}{5}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AB}

    \overrightarrow{NP} = \overrightarrow{NC} + \overrightarrow{CP}

    = \frac{2}{5}\overrightarrow{AC} - \left( \overrightarrow{BP} - \overrightarrow{BC} ight)

    = \frac{2}{5}\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{BC}

    = \frac{2}{5}\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\left( \overrightarrow{AC} - \overrightarrow{AB} ight)

    = \left( \frac{1}{k} - \frac{2}{5} ight)\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{AB}

    Để ba điểm M,N,Pthẳng hàng thì \exists m\mathbb{\in R}:\overrightarrow{NP} = m\overrightarrow{MN} hay

    \left( \frac{1}{k} - \frac{2}{5} ight)\overrightarrow{AC} + \left( \frac{1}{k} - 1 ight)\overrightarrow{AB} = \frac{3m}{5}\overrightarrow{AC} - \frac{m}{2}\overrightarrow{AB}

    \left\{ \begin{matrix}\dfrac{1}{k} - \dfrac{2}{5} = \dfrac{3m}{5} \\\dfrac{1}{k} - 1 = - \dfrac{m}{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}m = 4 \\k = \dfrac{1}{3} \\\end{matrix} ight.

  • Câu 12: Vận dụng cao

    Tam giác ABC thỏa mãn đẳng thức

    \dfrac{a^{2}\cos\dfrac{B -C}{2}}{2\sin\dfrac{A}{2}} + \dfrac{b^{2}\cos\dfrac{C -A}{2}}{2\sin\dfrac{B}{2}} + \dfrac{b^{2}\cos\dfrac{A -B}{2}}{2\sin\dfrac{C}{2}} = a^{2} + b^{2} + c^{2}

    Biết AB = c;BC = a;AC = b. Chọn khẳng định nào dưới đây đúng?

    Ta có:

    \dfrac{a^{2}\cos\dfrac{B -C}{2}}{2\sin\dfrac{A}{2}} = \dfrac{a\left( 2R\sin A ight)\cos\dfrac{B -C}{2}}{2\sin\dfrac{A}{2}}

    = 2aR.\cos\dfrac{A}{2}\cos\dfrac{B -C}{2}

    = 2aR.\sin\dfrac{B + C}{2}\cos\dfrac{B -C}{2}

    = aR.\left( \sin B + \sin C ight) = \frac{a(b + c)}{2}

    Chứng minh tương tự và suy ra ta có:

    \dfrac{a^{2}\cos\dfrac{B -C}{2}}{2\sin\dfrac{A}{2}} + \dfrac{b^{2}\cos\dfrac{C -A}{2}}{2\sin\dfrac{B}{2}} + \dfrac{b^{2}\cos\dfrac{A -B}{2}}{2\sin\dfrac{C}{2}}

    = \frac{a(b + c)}{2} + \frac{b(c + a)}{2} + \frac{c(a + b)}{2}

    = ab + bc + ca

    \leq \frac{a^{2} + b^{2}}{2} + \frac{b^{2} + c^{2}}{2} + \frac{c^{2} + a^{2}}{2} = a^{2} + b^{2} + c^{2}

    Dấu bằng xảy ra khi và chỉ khi a = b = c

    Vậy tam giác ABC là tam giác đều.

  • Câu 13: Nhận biết

    Trong mặt phẳng tọa độ Oxy cho P( - 3;1),Q(6; - 4). Xác định tọa độ trọng tâm H của tam giác OPQ?

    Vì H là trọng tâm tam giác OPQ nên ta có:

    \left\{ \begin{matrix}x_{H} = \dfrac{x_{O} + x_{P} + x_{Q}}{3} \\y_{H} = \dfrac{y_{O} + y_{P} + y_{Q}}{3} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x_{H} = \dfrac{0 - 3 + 6}{3} = 1 \\y_{H} = \dfrac{0 + 1 - 4}{3} = - 1 \\\end{matrix} ight.

    \Leftrightarrow H(1; - 1)

    Vậy trọng tâm tam giác cần tìm là H(1; - 1).

  • Câu 14: Thông hiểu

    Cho hàm số f(x) = \left\{ \begin{matrix} \frac{2x + 3}{x + 1} & khi & x \geq 0 \\ \frac{\sqrt[3]{2 + 3x}}{x - 2} & khi & - 2 \leq x < 0 \\ \end{matrix} ight.. Ta có kết quả nào sau đây đúng?

    f( - 1) = \frac{\sqrt[3]{2 - 3}}{- 1 - 2} = \frac{1}{3}; f(2) = \frac{2.2 + 3}{2 + 1} = \frac{7}{3}.

  • Câu 15: Nhận biết

    Trong mặt phẳng tọa độ Oxy, cho hai vectơ \overrightarrow{a} = ( - 2; - 1) và \overrightarrow{b} = (4; - 3). Tính cosin của góc giữa hai vectơ \overrightarrow{a} và \overrightarrow{b}.

    Ta có: \cos\left( \overrightarrow{a};\overrightarrow{b} ight) = \frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} ight|.\left| \overrightarrow{b} ight|} = \frac{- 5}{\sqrt{5}.5} = \frac{- \sqrt{5}}{5}.

  • Câu 16: Vận dụng cao

    Cho tam giác ABC có \widehat{A} = 90^{0}. Gọi các vectơ \overrightarrow{\alpha};\overrightarrow{\beta};\overrightarrow{\lambda} theo thư tự là các vectơ có giá vuông góc với các đường thẳng AB.AC,BC và \left| \overrightarrow{\alpha} ight| = AB;\left| \overrightarrow{\beta} ight| = AC;\left| \overrightarrow{\lambda} ight| = BC. Tính độ dài vectơ \overrightarrow{\alpha} + \overrightarrow{\beta} - \overrightarrow{\lambda}, biết AB = 3,AC = 4.

    Hình vẽ minh họa:

    Gọi D là điểm thuộc miền trong tam giác ABC, dựng các vectơ \overrightarrow{\alpha} = \overrightarrow{DG};\overrightarrow{\beta} = \overrightarrow{DE};\overrightarrow{\lambda} = \overrightarrow{DF} dựng hình chữ nhật DGHE ta có: \overrightarrow{\alpha} + \overrightarrow{\beta} = \overrightarrow{DH}

    Ta lại có: \Delta GDH = \Delta ABC \Rightarrow \widehat{GDH} = \widehat{ABC}

    Mặt khác \widehat{GDF} + \widehat{ABC} = 180^{0}

    \Rightarrow \widehat{GDF} + \widehat{GDH} = 180^{0}

    => Ba điểm H, D, F thẳng hàng.

    Khi đó: \left| \overrightarrow{\alpha} + \overrightarrow{\beta} - \overrightarrow{\lambda} ight| = \left| \overrightarrow{DH} + \overrightarrow{FD} ight| = \left| \overrightarrow{FH} ight| = 10

  • Câu 17: Thông hiểu

    Cho hai vectơ \overrightarrow{a} và \overrightarrow{b} khác \overrightarrow{0}. Xác định góc \alpha giữa hai vectơ \overrightarrow{a} và \overrightarrow{b} khi \overrightarrow{a}.\overrightarrow{b} = - \left| \overrightarrow{a} ight|.|\overrightarrow{b}|.

    Ta có \overrightarrow{a}.\overrightarrow{b} = \left|\overrightarrow{a} ight|.\left| \overrightarrow{b}ight|.\cos(\overrightarrow{a},\overrightarrow{b}).

    Mà theo giả thiết \overrightarrow{a}.\overrightarrow{b} = - \left|\overrightarrow{a} ight|.|\overrightarrow{b}|

    Suy ra \cos(\overrightarrow{a},\overrightarrow{b}) = - 1\longrightarrow (\overrightarrow{a},\overrightarrow{b}) =180^{\circ}

  • Câu 18: Nhận biết

    Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?

    Bất phương trình bậc hai một ẩn là: 3x^{2} – 12x + 1 ≤ 0

  • Câu 19: Thông hiểu

    Tập hợp B=(2;+∞)\cup [-3;8] bằng tập hợp nào sau đây?

     Xác định kết quả tập hợp bằng hình vẽ như sau:

    Xác định tập hợp

    Vậy B=(2;+∞)\cup [-3;8] =[-3;+∞)

  • Câu 20: Thông hiểu

    Cho hình vuông ABCD. Khẳng định nào sau đây đúng?

    ABCD là hình vuông \Rightarrow \overrightarrow{AD} = \overrightarrow{BC} = - \overrightarrow{CB} \Rightarrow \left| \overrightarrow{AD} ight| = \left| \overrightarrow{CB} ight|.

  • Câu 21: Thông hiểu

    Số nghiệm của phương trình \sqrt{x + 12} - \sqrt{x - 3} = \sqrt{2x +1} là

    ĐK x ≥ 3.

    \sqrt{x + 12} - \sqrt{x - 3} = \sqrt{2x+ 1}

    \Leftrightarrow \sqrt{x + 12} = \sqrt{x- 3} + \sqrt{2x + 1}

    \Leftrightarrow \sqrt{(x - 3)(2x + 1)} =- x + 7

    \Leftrightarrow \left\{ \begin{matrix}x \leq 7 \\2x^{2} - 5x - 3 = x^{2} - 14x + 49 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}x \leq 7 \\x^{2} + 9x - 52 = 0 \\\end{matrix} ight.

    \Leftrightarrow \left\lbrack\begin{matrix}x = 4(TM) \\x = - 13(KTM) \\\end{matrix} ight..

    Vậy phương trình có một nghiệm.

  • Câu 22: Nhận biết

    Tìm tất cả các giá trị của m để hàm số y = f(x) = (2-m)x+x + 2 nghịch biến trên \mathbb{R}.

     Điều kiện để hàm số y=ax+b nghịch biến trên \mathbb {R} là a<0.

    Suy ra 2-m<0 \Leftrightarrow m>2.

  • Câu 23: Nhận biết

    Trên đường thẳng MN lấy điểm P sao cho \overrightarrow{MN} = - 3\overrightarrow{MP}. Điểm P được xác định đúng trong hình vẽ nào sau đây:

    Ta có \overrightarrow{MN} = - 3\overrightarrow{MP} nên MN = 3MP và \overrightarrow{MN} và \overrightarrow{MP} ngược hướng.

  • Câu 24: Vận dụng

    Hàm số y =  − x2 + 2(m−1)x + 3 nghịch biến trên (1;+∞) khi giá trị m thỏa mãn:

    Đồ thị hàm số có trục đối xứng là đường x = m − 1. Đồ thị hàm số đã cho có hệ số x2 âm nên sẽ đồng biến trên (−∞;m−1) và nghịch biến trên (m−1;+∞). Theo đề, cần: m − 1 ≤ 1 ⇔ m ≤ 2.

  • Câu 25: Nhận biết

    Cho hình bình hành ABCD. Với mọi điểm M, ta có khẳng định nào sau đây:

     Ta có: \overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{MC}-\overrightarrow{MD} \Leftrightarrow \overrightarrow {AB}= \overrightarrow {DC} (Đúng).

  • Câu 26: Thông hiểu

    Trong mặt phẳng tọa độ Oxy, cho tọa độ các điểm M( - 3;1),N(1;4),P(5;3). Xác định tọa độ điểm Q sao cho tứ giác MNPQ là hình bình hành?

    Gọi tọa độ điểm Q(x;y)

    Ta có: \left\{ \begin{matrix} \overrightarrow{MQ} = (x + 3;y - 1) \\ \overrightarrow{NP} = (4; - 1) \\ \end{matrix} ight.

    Vì MNPQ là hình bình hành nên

    \overrightarrow{MQ} = \overrightarrow{NP} \Leftrightarrow \left\{ \begin{matrix} x + 3 = 4 \\ y - 1 = - 1 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 1 \\ y = 0 \\ \end{matrix} ight.

    Vậy tọa độ điểm Q cần tìm là Q(1;0).

  • Câu 27: Nhận biết

    Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có đỉnh I\left( - \frac{1}{2}; - \frac{11}{4} ight).

    Vì (P) có đỉnh I\left( - \frac{1}{2}; - \frac{11}{4} ight) nên ta có \left\{ \begin{matrix} - \frac{b}{2a} = - \frac{1}{2} \\ f\left( - \frac{1}{2} ight) = - \frac{11}{4} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} b = a \\ \Delta = 11a \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 3 = a \\ 9 + 8a = 11a \\ \end{matrix} ight.\ \Leftrightarrow a = 3. Vậy (P) : y = 3x2 + 3x − 2.

  • Câu 28: Thông hiểu

    Miền nghiệm của hệ bất phương trình \left\{ \begin{matrix} \frac{5x}{2} + \frac{4y}{3} - 1 \geq 0 \\ y > 0 \\ 2x - \frac{3y}{2} > 5 \\ \end{matrix} ight. chứa điểm nào trong các điểm sau đây?

    Với P(5;2). Ta có: \left\{ \begin{matrix} \frac{5.5}{2} + \frac{4.2}{3} - 1 \geq 0 \\ 2 > 0 \\ 2.5 - \frac{3.2}{2} > 5 \\ \end{matrix} ight.. Cả ba bất phương trình đều đúng. Chọn đáp án này.

  • Câu 29: Vận dụng

    Cho hai lực \overrightarrow{F_1} và \overrightarrow{F_2} cùng tác động vào một vật đứng tại điểm O, biết hai lực \overrightarrow{F_1} và \overrightarrow{F_2} đều có cường độ là 50 (N) và chúng hợp với nhau một góc 60°. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?

     

    Đặt \overrightarrow {AB},\overrightarrow {AC},\overrightarrow {AD} tương ứng với các vectơ\overrightarrow {F} như hình vẽ.

    Ta có: \left| {\overrightarrow {AB} + \overrightarrow {AC} } ight| = \left| {\overrightarrow {AB} + \overrightarrow {BD} } ight| = \left| {\overrightarrow {AD} } ight| = AD.

    Theo đề bài, góc \widehat{B AC} bằng 60 độ. Suy ra \hat B=120^{\circ}.

    A{D^2} = A{B^2} + B{D^2} - 2.AB.BD.\cos 60^\circ = 7500. Suy ra AD=50\sqrt3N.

     

     

  • Câu 30: Nhận biết

    Với \overrightarrow{DE} (khác vectơ - không) thì độ dài đoạn ED được gọi là

    Với \overrightarrow{DE} (khác vectơ - không) thì độ dài đoạn ED được gọi là: Độ dài của \overrightarrow{ED}.

  • Câu 31: Vận dụng

    Cho hai tập hợp A = \left\{ x\mathbb{\in R}:x + 3 < 4 + 2x ight\} và B = \left\{ x\mathbb{\in R};5x - 3 < 4x - 1 ight\}. Tìm tất cả các số tự nhiên thuộc cả hai tập A và B.

    x + 3 < 4 + 2x \Leftrightarrow x > - 1 \Rightarrow A = ( - 1; + \infty).

    5x - 3 < 4x - 1 \Leftrightarrow x < 2 \Rightarrow B = ( - \infty;2).

    \Rightarrow A \cap B = ( - 1;2) \Rightarrow Có hai số tự nhiên thuộc cả hai tập A và B là 0 và 1.

  • Câu 32: Thông hiểu

    Cho tam giác ABC có M là trung điểm của BC. Tính \overrightarrow{AB} theo \overrightarrow{AM} và \overrightarrow{BC}.

    Ta có \overrightarrow{AB} = \overrightarrow{AM} + \overrightarrow{MB} = \overrightarrow{AM} - \frac{1}{2}\overrightarrow{BC}.

  • Câu 33: Thông hiểu

    Cho \overrightarrow{u} = (3; - 2),\ \overrightarrow{v} = (1;6). Khẳng định nào sau đây là đúng?

    Ta có \overrightarrow{u} + \overrightarrow{v} = (4;4) và \overrightarrow{u} - \overrightarrow{v} = (2; - 8).

    Xét tỉ số \frac{4}{- 4} eq \frac{4}{4}\overset{}{ightarrow}\overrightarrow{u} + \overrightarrow{v} và \overrightarrow{a} = ( - 4;4) không cùng phương. Loại \overrightarrow{u} + \overrightarrow{v} và \overrightarrow{a} = ( - 4;4) ngược hướng.

    Xét tỉ số \frac{3}{1} eq \frac{- 2}{6}\overset{}{ightarrow}\overrightarrow{u},\ \overrightarrow{v} không cùng phương. Loại \overrightarrow{u},\ \overrightarrow{v} cùng phương.

    Xét tỉ số \frac{2}{6} = \frac{- 8}{- 24} = \frac{1}{3} > 0\overset{}{ightarrow}\overrightarrow{u} - \overrightarrow{v} và \overrightarrow{b} = (6; - 24) cùng hướng. Chọn \overrightarrow{u} - \overrightarrow{v} và \overrightarrow{b} = (6; - 24) cùng hướng.

  • Câu 34: Thông hiểu

    Bảng xét dấu sau đây là của tam thức bậc hai nào?

    Từ bảng xét dấu ta có:

    f(x) = 0 có hai nghiệm phân biệt x = 2;x = 3 và f(x) > 0 khi x \in (2;3)

    Do đó f(x) = - x^{2} + 5x - 6

  • Câu 35: Vận dụng

    Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60^{0}. Tàu thứ nhất chạy với tốc độ 30\ km/h, tàu thứ hai chạy với tốc độ 40\ km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

    Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: S_{1} = 30.2 = 60\ km.

    Sau 2h quãng đường tàu thứ hai chạy được là: S_{2} = 40.2 = 80\ km.

    Vậy: sau 2h hai tàu cách nhau là: S = \sqrt{{S_{1}}^{2} + {S_{2}}^{2} - 2S_{1}.S_{2}.cos60^{0}} = 20\sqrt{13}.

  • Câu 36: Vận dụng

    Cho hệ bất phương trình \left\{\begin{matrix}x+5y<1\\ 5x-4y>6\end{matrix}ight.. Hỏi khi cho y = 0, x có thể nhận mấy giá trị nguyên nào?

    Khi y=0 hệ bất phương trình trở thành:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {x + 5.0 < 1} \\ {5x - 4.0 > 6} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x < 1} \\ {5x > 6} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x < 1} \\ {x > \dfrac{6}{5}} \end{array}} ight.\left( {VN} ight) \Rightarrow x \in \left\{ \emptyset ight\} \hfill \\ \end{matrix}

    Vậy y=0 không có giá trị nguyên nào của x thỏa mãn hệ bất phương trình đã cho.

  • Câu 37: Nhận biết

    Trong các cặp số sau, cặp số nào không là nghiệm của hệ bất phương trình \left\{\begin{matrix}x+y-2\leq 0\\ 2x-3y+2>0\end{matrix}ight.

     Thay cặp số (–1;1) vào hệ ta được \left\{\begin{matrix}-1+1-2\leq 0\\ 2(-1)-3.1+2>0\end{matrix}ight. không thỏa mãn bất phương trình ở dưới. Do đó cặp số này không là nghiêm của hệ.

  • Câu 38: Nhận biết

    Tìm đáp án không phải mệnh đề trong các câu sau.

    Câu “Bộ phim quá hay!” là câu cảm thán nên không phải là mệnh đề.

  • Câu 39: Nhận biết

    Cho biết \tan\alpha = \frac{1}{2}. Tính \cot\alpha.

    Ta có: \tan\alpha.cot\alpha = 1 \Rightarrow \cot\alpha = \frac{1}{\tan\alpha} = \frac{1}{\frac{1}{2}} = 2.

  • Câu 40: Nhận biết

    Tam giác ABC có \widehat{B} = 60^{\circ},\widehat{C} = 45^{\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí sin ta có:

    \frac{AB}{\sin C} = \frac{AC}{\sin B} \Leftrightarrow \frac{5}{\sin 45^{\circ}} = \frac{AC}{\sin 60^{\circ}}

    \Leftrightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 41: Vận dụng

    Phương trình \sqrt{x} + \sqrt{9 - x} = \sqrt{- x^{2} + 9x +9} có mấy nghiệm ?

    Điều kiện: 0 ≤ x ≤ 9

    Bình phương hai vế phương trình đã cho ta được:

    \begin{matrix}x + 2\sqrt{9x - x^{2}} + 9 - x = - x^{2} + 9x + 9 \\\Leftrightarrow 2\sqrt{9x - x^{2}} = - x^{2} + 9x \\\end{matrix}

    Đặt t = \sqrt{9x - x^{2}}\ \ \ \ (t \geq0). PT trên trở thành: 2t = t^{2}\Leftrightarrow \left\lbrack \begin{matrix}t = 0 \\t = 2 \\\end{matrix} ight.

    Với t = 0 \Rightarrow \sqrt{9x - x^{2}} =0 \Leftrightarrow \left\lbrack \begin{matrix}x = 0 \\x = 9 \\\end{matrix} ight. (TM)

    Với t = 2 \Rightarrow \sqrt{9x - x^{2}} =2 \Leftrightarrow \left\lbrack \begin{matrix}x = \frac{9 + \sqrt{65}}{2} \\x = \frac{9 - \sqrt{65}}{2} \\\end{matrix} ight. (TM)

    Vậy phương trình có tập nghiệm là S =\left\{ 0;9;\frac{9 \pm \sqrt{65}}{2} ight\} (3 nghiệm).

  • Câu 42: Vận dụng

    Cho hai vectơ \overrightarrow{a}và \overrightarrow{b}. Biết \left| \overrightarrow{a} ight| =2 , \left| \overrightarrow{b} ight|= \sqrt{3} và \left( \overrightarrow{a},\overrightarrow{b} ight) = 120^{o}. Tính\left| \overrightarrow{a} + \overrightarrow{b} ight|.

    Ta có: \left| \overrightarrow{a} + \overrightarrow{b} ight| = \sqrt{\left( \overrightarrow{a} + \overrightarrow{b} ight)^{2}} = \sqrt{{\overrightarrow{a}}^{2} + {\overrightarrow{b}}^{2} + 2\overrightarrow{a}.\overrightarrow{b}} = \sqrt{\left| \overrightarrow{a} ight|^{2} + \left| \overrightarrow{b} ight|^{2} + 2\left| \overrightarrow{a} ight|\left| \overrightarrow{b} ight|\ \ cos\left( \overrightarrow{a},\overrightarrow{b} ight)} = \sqrt{7 - 2\sqrt{3}}.

  • Câu 43: Nhận biết

    Cách viết tập hợp nào đúng trong các cách viết sau để xác định tập hợp A các ước dương của 12:

    Các ước dương của 12 là: 1; 2; 3; 4; 6; 12

    => Cách viết tập hợp đúng là: A = \left \{ 1; 2; 3; 4; 6; 12ight \}

  • Câu 44: Thông hiểu

    Tam giác ABC có AB = \sqrt{2},\ \ AC = \sqrt{3} và \widehat{C} = 45{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{C}

    \Rightarrow \left( \sqrt{2} ight)^{2} = \left( \sqrt{3} ight)^{2} + BC^{2} - 2.\sqrt{3}.BC.cos45{^\circ}

    \Rightarrow BC = \frac{\sqrt{6} + \sqrt{2}}{2}.

  • Câu 45: Thông hiểu

    Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:

    Áp dụng hệ quả định lí cosin cho tam giác ABC ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \hfill \\ \Rightarrow \cos \widehat A = \dfrac{{{{15}^2} + {{13}^2} - {{24}^2}}}{{2.15.13}} = - \dfrac{7}{{15}} \hfill \\ \Rightarrow \widehat A \approx {117^0}49\prime \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Cánh Diều Đề 1 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 34 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 10 Cánh Diều Đề 1
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập