Cho tam giác ![]() vuông tại
vuông tại ![]() có
có ![]() . Tính độ dài
. Tính độ dài ![]() .
.
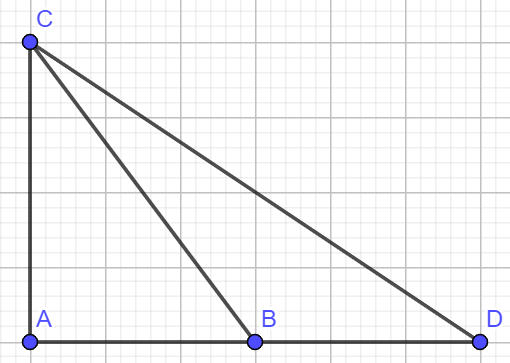
Đặt .
Ta có: .
Áp dụng định lý Pytago trong tam giác :
.
Cho tam giác ![]() vuông tại
vuông tại ![]() có
có ![]() . Tính độ dài
. Tính độ dài ![]() .
.

Đặt .
Ta có: .
Áp dụng định lý Pytago trong tam giác :
.
Tam giác ABC có ![]() . Số đo góc A là:
. Số đo góc A là:
Áp dụng định lí cosin trong tam giác ta có:
Cho hệ bất phương trình ![]() có tập nghiệm
có tập nghiệm ![]() . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
Ta có: . Do đó không có điểm nào thỏa mãn hệ phương trình.
Hệ này vô nghiệm.
Cho A là tập hợp các bội của 2, B là tập hợp các bội của 8. Chọn khẳng định đúng:
Số lượng phần tử của tập hợp các bội của 2 nhiều hơn số lượng phần tử tập hợp các bội của 8. Mà đã là bội của 8 thì cũng là bội của 2.
Do đó
Cho hai vectơ ![]() và
và ![]() đều khác vectơ
đều khác vectơ ![]() Tích vô hướng của
Tích vô hướng của ![]() và
và ![]() được xác định bằng công thức nào dưới đây?
được xác định bằng công thức nào dưới đây?
Cho hai vectơ và
đều khác vectơ
Tích vô hướng của
và
là một số, kí hiệu là
được xác định bởi công thức sau:
.
Trong mặt phẳng ![]() , cho
, cho ![]() và
và ![]() . Khẳng định nào sau đây là sai?
. Khẳng định nào sau đây là sai?
Ta có: nên đáp án Tích vô hướng của hai vectơ đã cho là
đúng.
Ta có: nên đáp án Độ lớn của vectơ
là
đúng.
Ta có: nên đáp án Độ lớn của vectơ
là
đúng.
Đáp án sai là Góc giữa hai vectơ là .
Cho tam giác ![]() với
với ![]() là trung điểm
là trung điểm ![]() Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
Xét đáp án Ta có
(theo quy tắc ba điểm).
Chọn đáp án này.
Trong mặt phẳng Oxy cho ![]() ,
, ![]() ,
, ![]() . Khẳng định nào sau đây đúng.
. Khẳng định nào sau đây đúng.
Do nên loại đáp án
.
Do,
,
suy ra
không vuông góc
nên loại đáp án
.
Ta có ,
,
, suy ra
,
. Do đó tam giác
vuông cân tại
.
Tìm tất cả giá trị của tham số ![]() để hệ bất phương trình
để hệ bất phương trình  có tập nghiệm được biểu diễn trên mặt phẳng tọa độ là một hình tam giác.
có tập nghiệm được biểu diễn trên mặt phẳng tọa độ là một hình tam giác.
Họ đường thẳng luôn đi qua điểm
, hay nói cách khác các đường thẳng
xoay quanh A.
Mặt khác, ta có đúng với mọi m
=> Miền nghiệm của bất phương trình luôn chứa điểm
.
Do đó ta có 3 khả năng sau
Vậy .
Cho đoạn thẳng ![]() và
và ![]() là một điểm trên đoạn
là một điểm trên đoạn ![]() sao cho
sao cho ![]() . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai?
Hình vẽ minh họa
Ta thấy và
cùng hướng nên
là sai.
Cho tam giác ![]() có
có ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Áp dụng định lí côsin:
.
Suy ra .
Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có trục đối xứng x = − 3.
Vì (P) có trục đối xứng x = − 3 nên .
Vậy .
Cho tập hợp ![]() và
và ![]() Tập hợp
Tập hợp ![]() bằng tập nào sau đây?
bằng tập nào sau đây?
Tập hợp gồm những phần tử thuộc
nhưng không thuộc
.
Số nghiệm của phương trình ![]()
Điều kiện
Phương trình tương đương:
Do
Vậy phương trình vô nghiệm.
Giá trị lớn nhất ![]() của biểu thức
của biểu thức ![]() trên miền xác định bởi hệ
trên miền xác định bởi hệ  là
là
Trong mặt phẳng tọa độ vẽ các đường thẳng
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
Ta có
Số nghiệm của phương trình ![]() là:
là:
vô số.
Ta thấy x = − 3 không là nghiệm của phương trình.
Xét x ≠ − 3, phương trình
Phương trình (*)
(thỏa mãn)
Vậy phương trình đã cho có hai nghiệm x = 0 và .
Trong các đáp án dưới đây, cách viết khác của tập D = {x ∈ ℝ | x ≠ -3} là
Ta có: D = {x ∈ ℝ | x ≠ -3} = ℝ \ {-3}.
Đâu là kí hiệu của hai mệnh đề kéo theo?
Mệnh đề kéo theo được kí hiệu là:
Cho tam giác ![]() , chọn công thức đúng trong các đáp án sau:
, chọn công thức đúng trong các đáp án sau:
Ta có:
Điểm cuối của ![]() thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
Điểm cuối của thuộc góc phần tư thứ nhất
.
Trong mặt phẳng tọa độ Oxy cho 2 điểm M(2; 1) và N(1; 2). Tọa độ vectơ ![]() là
là
Ta có:
Tất cả các giá trị của tham số m để phương trình ![]() có nghiệm là:
có nghiệm là:
ĐKXĐ: x ≥ 1 .
Chia cả hai vế cho ta có
Đặt
Phương trình trở thành − 3t2 + 2t = m (*)
Xét hàm số y = − 3t2 + 2t trên [0; 1) , ta có ,
Bảng biến thiên
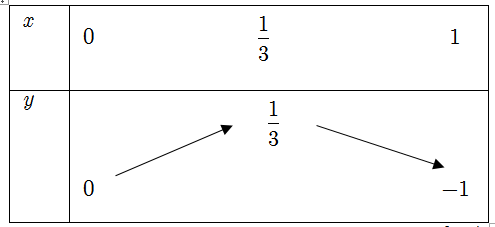
Phương trình ban đầu có nghiệm ⇔ phương trình (*) có nghiệm t∈ [0; 1)
⇔ đồ thị hàm số y = − 3t2 + 2t trên [0; 1) cắt đường thẳng
Vậy phương trình ban đầu có nghiệm khi và chỉ khi .
Tam thức bậc hai ![]() nhận giá trị dương khi và chỉ khi
nhận giá trị dương khi và chỉ khi
Ta có: và
.
Phươn trình có hai nghiệm phân biệt
.
Do đó
.
Hai vectơ được gọi là bằng nhau khi và chỉ khi
Hai vectơ được gọi là bằng nhau khi và chỉ khi: Chúng cùng hướng và độ dài của chúng bằng nhau.
Giải bất phương trình ![]()
Ta có bảng xét dấu như sau:
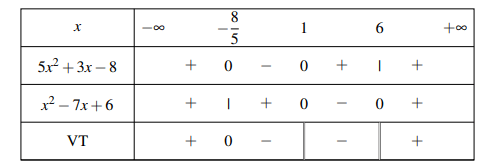
Vậy tập nghiệm của bất phương trình là:
Tập nghiệm S của bất phương trình ![]() là:
là:
Ta có: .
Suy ra .
Cặp nghiệm nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: ![]() ?
?
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án sai
=>
thay vào bất phương trình ta có:
=> Đáp án đúng
Vậy là nghiệm của bất phương trình bậc nhất hai ẩn:
Tam thức bậc hai ![]() nhận giá trị dương khi và chỉ khi
nhận giá trị dương khi và chỉ khi
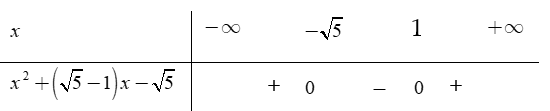
Dựa vào bảng xét dấu, ta chọn đáp án
Cho hình bình hành ABCD tâm O. Khi đó ![]() bằng:
bằng:
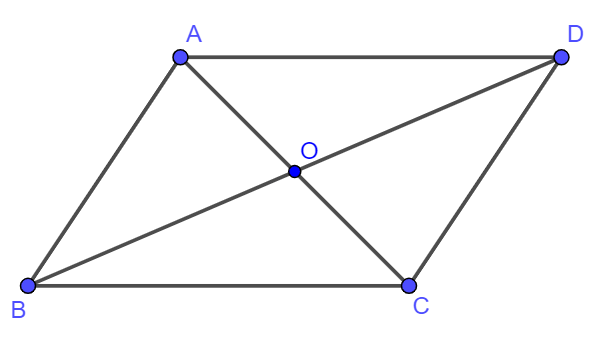
Ta có:
Trong hệ tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() . Tìm tọa độ đỉnh
. Tìm tọa độ đỉnh ![]() ?
?
Gọi .
Từ giả thiết, ta suy ra
Ta có và
Khi đó
Tìm tất cả các giá trị thực của tham số m để phương trình x2 − (m−1)x + m + 2 = 0 có hai nghiệm phân biệt x1, x2 khác 0 thỏa mãn ![]()
Đặt f(x) = x2 − (m−1)x + m + 2
Phương trình có hai nghiệm phân biệt khác 0 khi và chỉ khi:
Theo Viet, ta có .
Yêu cầu bài toán
.
Kết hợp điều kiện ta được m ∈ (−∞;−2) ∪ (−2;−1).
Cho ![]() Tìm
Tìm ![]()
Vậy .
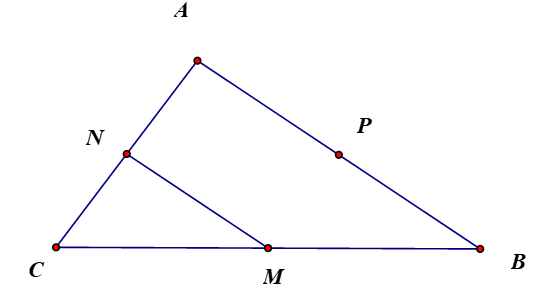
Cho tam giác ![]() điểm
điểm ![]() thuộc cạnh
thuộc cạnh ![]() sao cho
sao cho ![]() và
và ![]() là trung điểm của
là trung điểm của ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]()
Vì là trung điểm
nên
Suy ra
Tập xác định của hàm số ![]() là:
là:
Hàm số xác định . Vậy D = ℝ ∖ {0;4}.
Có bao nhiêu mệnh đề trong các câu sau?
Ở đây đẹp quá!
Phương trình ![]() vô nghiệm.
vô nghiệm.
16 không là số nguyên tố.
Số ![]() có lớn hơn
có lớn hơn ![]() hay không?
hay không?
Câu “Phương trình vô nghiệm.” và “16 không là số nguyên tố.” là mệnh đề.
Biết phương trình ![]() có hai nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây là đúng?
có hai nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây là đúng?
Đặt t = x2 − 3x + 3, ta có: .
Do đó điều kiện cho ẩn phụ t là .
Khi đó phương trình trở thành:
⇔
⇔
⇔ t = 1(thỏa mãn)
⇒ x2 − 3x + 3 = 1⇔ .
Cho ![]() ,
,![]() . Tính góc của
. Tính góc của ![]() .
.
Ta có .
Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Hàm số bậc hai y = x2 – 3x + 2 có tập xác định là ℝ. Khẳng định "Tập xác định của hàm số là D = (0; +∞)." sai.
Xét điểm M(1; 0): thay x = 1; y = 0 vào hàm số ta có: 0 = 12 – 3. 1 + 2 = 0 là mệnh đề đúng. Vậy M(1; 0) thuộc đồ thị hàm số. Khẳng định "Điểm M(1; 0) thuộc đồ thị hàm số." đúng.
Hàm số y = x2 – 3x + 2 có a = 1 > 0, b = ‒3 nên hàm số nghịch biến trên khoảng và đồng biến trên khoảng
. Khẳng định "Hàm số đồng biến trên ℝ." sai.
Hàm số y = x2 – 3x + 2 có a = 1 > 0 nên đồ thị hàm số có bề lõm quay lên trên. Khẳng định "Đồ thị hàm số có bề lõm quay xuống dưới." sai.
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() có
có ![]() . Tính
. Tính ![]()
Gọi là trung điểm
Ta có
Cho hệ bất phương trình ![]() . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với
.Bất phương trình thứ hai sai nên không thỏa mãn.
Với
. Đúng.
Trong hệ tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() và trọng tâm là gốc tọa độ
và trọng tâm là gốc tọa độ ![]() Tìm tọa độ đỉnh
Tìm tọa độ đỉnh ![]() ?
?
Gọi .
Vì là trọng tâm tam giác
nên
Trong các tập hợp sau đây, tập hợp nào không phải là con của tập hợp A với ![]() {
{![]() ,
, ![]() và
và ![]() }
}
Ta liệt kê các phần tử của tập A: .
Như vậy chỉ có phương án là tập hợp có các phần tử 1, 2, 3 không thuộc tập A nên không là tập con của A.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x4 − 4x3 − x2 + 10x − 3 trên đoạn [ − 1; 4] là
Ta có y = x4 − 4x3 − x2 + 10x − 3 = x4 − 4x3 + 4x2 − 5x2 + 10x − 5 + 2
= (x2−2x)2 − 5(x−1)2 + 2 = [(x−1)2−1]2 − 5(x−1)2 + 2.
Đặt t = (x−1)2, x ∈ [ − 1; 4] ⇒ t ∈ [0; 9].
.
Cách 1: Ta có .
Cách 2: Vẽ BBT
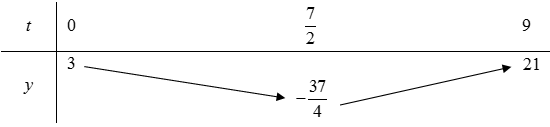
Vậy , ymax = 21.
Cặp số ![]() không là nghiệm của bất phương trình nào sau đây?
không là nghiệm của bất phương trình nào sau đây?
Xét đáp án
Thay ta được:
Vậy cặp số không là nghiệm của bất phương trình.
Xét đáp án
Thay ta được:
Vậy cặp số là nghiệm của bất phương trình.
Xét đáp án
Thay ta được:
Vậy cặp số là nghiệm của bất phương trình.
Xét đáp án
Thay ta được:
Vậy cặp số là nghiệm của bất phương trình.
Cho ![]() vuông tại
vuông tại ![]() và có
và có ![]() . Số đo của góc
. Số đo của góc ![]() là:
là:
Ta có: Trong
.
