Lớp 10 Toán 10 - Cánh diều

Đề thi học kì 1 Toán 10 Cánh Diều Đề 3

Mô tả thêm: Đề thi học kì 1 Toán 10 được biên soạn gồm 45 câu hỏi bám sát 4 chuyên đề giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức môn Toán lớp 10 sách Cánh Diều.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Cho tam giác ABC có AB=1;AC=\sqrt2;\hat A=45^{\circ}. Tính độ dài cạnh BC.

     Áp dụng định lí côsin:

    BC^2=AB^2+AC^2-2.AB.AC.\cos A=1+2-2.1.\sqrt2.\cos45^{\circ} =1.

    Suy ra BC=1.

  • Câu 2: Nhận biết

    Trong mặt phẳng tọa độ Oxy cho điểm C có tọa độ là C(‒2; ‒5). Biểu diễn vectơ \overrightarrow{OC} theo các vectơ đơn vị là

    \begin{matrix} O\left( {0;0} ight) \hfill \\ \overrightarrow {OC} = \left( {{x_C} - {x_O};{y_C} - {y_O}} ight) = \left( { - 2; - 5} ight) \hfill \\ \Rightarrow \overrightarrow {OC} = - 2\overrightarrow i - 5\overrightarrow j \hfill \\ \end{matrix}

  • Câu 3: Nhận biết

    Cho tam thức bậc hai f(x) = {x^2} - 10x + 2. Kết luận nào sau đây đúng?

    Ta có:

    \begin{matrix}f\left( { - 2} ight) = {\left( { - 2} ight)^2} - 10.\left( { - 2} ight) + 2 = 26 > 0 \hfill \\ f\left( 1 ight) = {\left( 1 ight)^2} - 10.\left( 1 ight) + 2 = - 7 < 0 \hfill \\ \end{matrix}

    Vậy khẳng định đúng là f(–2) > 0.

  • Câu 4: Thông hiểu

    Cho tọa độ ba điểm A(0;3),B(4;0),C( - 2; - 5). Tính \overrightarrow{AB}.\overrightarrow{BC}?

    Ta có: A(0;3),B(4;0),C( - 2; - 5)

    \Rightarrow \left\{ \begin{matrix} \overrightarrow{AB} = (4; - 3) \\ \overrightarrow{BC} = ( - 6; - 5) \\ \end{matrix} ight.

    \Rightarrow \overrightarrow{AB}.\overrightarrow{BC} = 4.( - 6) + ( - 3).( - 5) = - 9

  • Câu 5: Nhận biết

    Kí hiệu nào sau đây dùng để viết đúng mệnh đề “\sqrt{2} không phải là số hữu tỉ”

    Ta có: \sqrt{\mathbf{2}}\mathbb{otin Q}\mathbf{.}

  • Câu 6: Nhận biết

    Cho hình bình hành ABCD tâm O. Khi đó \overrightarrow{OA}+\overrightarrow{BO} bằng:

     

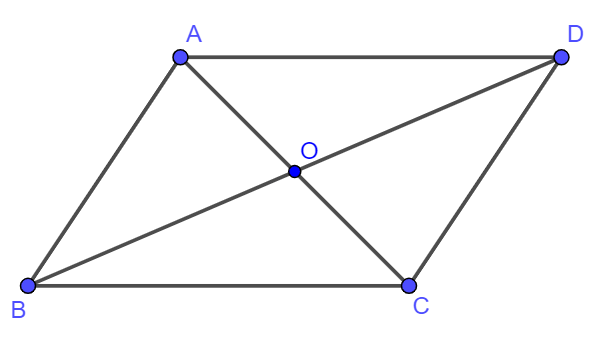
    Ta có: \overrightarrow {BO} + \overrightarrow {OA} = \overrightarrow {BA} = \overrightarrow {CD}

  • Câu 7: Vận dụng cao

    Cho tam giác ABC có AB = c;BC = a;AC = b và các góc của tam giác thỏa mãn biểu thức:

    \left\{ \begin{matrix}\sin\widehat{B}.\sin\widehat{C} = \dfrac{3}{4} \\a^{2} = \dfrac{a^{3} - b^{3} - c^{3}}{a - b - c} \\\end{matrix} ight.. Khi đó tam giác ABC là tam giác gì?

    Ta có:

    a^{2} = \frac{a^{3} - b^{3} - c^{3}}{a - b - c}

    \Leftrightarrow a^{2}(a - b - c) = a^{3} - b^{3} - c^{3}

    \Leftrightarrow a^{2}(a + b) = (b + c)\left( b^{2} - bc + c^{2} ight)

    \Leftrightarrow a^{2} = b^{2} - bc + c^{2}

    \Leftrightarrow b^{2} + c^{2} - a^{2} = bc

    \Leftrightarrow \frac{b^{2} + c^{2} - a^{2}}{2bc} = \frac{1}{2}

    \Leftrightarrow \cos\widehat{A} = \frac{1}{2}

    \Leftrightarrow \widehat{A} = \frac{\pi}{3}(*)

    Ta lại có:

    \sin\widehat{B}.sin\widehat{C} = \frac{3}{4}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) - \cos\left( \widehat{B} + \widehat{C} ight) = \frac{3}{2}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) + \cos\widehat{A} = \frac{3}{2}

    \Leftrightarrow \cos\left( \widehat{B} - \widehat{C} ight) = 1

    \Leftrightarrow \widehat{B} - \widehat{C} = 0 \Leftrightarrow \widehat{B} = \widehat{C}

    Vậy tam giác ABC là tam giác đều.

  • Câu 8: Thông hiểu

    Trong hệ tọa độ Oxy, cho các điểm A(0;1),B(1;3),C(2;7). Xác định tọa độ điểm N thỏa mãn biểu thức \overrightarrow{AB} = 2\overrightarrow{AN} + 3\overrightarrow{CN}?

    Theo bài ra ta có:

    \overrightarrow{AB} = 2\overrightarrow{AN} + 3\overrightarrow{CN}

    \Leftrightarrow \overrightarrow{AO} + \overrightarrow{OB} = 2\overrightarrow{AO} + 2\overrightarrow{ON} + 3\overrightarrow{CO} + 3\overrightarrow{ON}

    \Leftrightarrow \overrightarrow{ON} = \frac{1}{5}\left( \overrightarrow{OA} + \overrightarrow{OB} + 2\overrightarrow{OC} ight)

    \Rightarrow N\left( \frac{1 + 6}{5};\frac{1 + 3 + 21}{5} ight) = \left( \frac{7}{5};5 ight)

  • Câu 9: Vận dụng

    Cho tam thức bậc hai f(x) = \left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1. Tìm tất cả các giá trị thực của tham số m để bất phương trình f(x) > 0 vô nghiệm?

    Bất phương trình: f(x) > 0\ (*) vô nghiệm khi và chỉ khi

    \left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1 \leq 0,\forall x\mathbb{\in R}

    Xét 2m^{2} + m - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = - 2 \\ m = \frac{3}{2} \\ \end{matrix} ight.

    Với m = - 2 thì (*) \Leftrightarrow - 7x - 1 > 0 \Leftrightarrow x < - \frac{1}{7} loại giá trị m = - 2.

    Với m = \frac{3}{2} thì bất phương trình (*) \Leftrightarrow 0x - 1 < 0 bất phương trình vô nghiệm, nhận giá trị m = \frac{3}{2}.

    Xét 2m^{2} + m - 6 eq 0

    \left( 2m^{2} + m - 6 ight)x^{2} + (2m - 3)x - 1 \leq 0,\forall x\mathbb{\in R}

    \Leftrightarrow \left\{ \begin{matrix} 2m^{2} + m - 6 < 0 \\ (2m - 3)^{2} - 4\left( 2m^{2} + m - 6 ight).( - 1) \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{gathered} - 2 < m < \dfrac{3}{2} \hfill \\ - \dfrac{5}{6} \leqslant m \leqslant \frac{3}{2} \hfill \\ \end{gathered} ight. \Leftrightarrow - \frac{5}{6} \leqslant m < \frac{3}{2}

    Vậy m \in \left\lbrack - \frac{5}{6};\frac{3}{2} ightbrack thì bất phương trình (*) vô nghiệm.

  • Câu 10: Thông hiểu

    Cho tam thức f(x) = ax^{2} + bx + c (a ≠ 0), có ∆ = b^{2} – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:

    Biểu thức f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:

    \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a < 0} \\ {\Delta ' \leqslant 0} \end{array}} ight.

  • Câu 11: Nhận biết

    Cặp số (1; – 1) là nghiệm của bất phương trình nào sau đây?

     Thay cặp số (1; – 1) vào bất phương trình x + 3y + 1< 0 ta được: -1 < 0 thỏa mãn. Suy ra cặp số này là nghiệm của bất phương trình.

  • Câu 12: Vận dụng

    Mệnh đề nào sau đây sai?

    Với ba điểm phân biệt A,\ \ B,\ \ C nằm trên một đường thẳng, đẳng thức \left| \overrightarrow{AB} ight| + \left| \overrightarrow{BC} ight| = \left| \overrightarrow{AC} ight| \Leftrightarrow AB + BC = AC xảy ra khi B nằm giữa A và C.

    Chọn đáp án sai là: Nếu ba điểm phân biệt A,B,C nằm tùy ý trên một đường thẳng thì \left| \overrightarrow{AB} ight| + \left|\overrightarrow{BC} ight| = \left| \overrightarrow{AC}ight|.

  • Câu 13: Vận dụng cao

    Tất cả các giá trị của tham số m để các nghiệm của phương trình \sqrt{x+1}-2=0\;(1) cũng là nghiệm của phương trình x2 − 2mx − m2 − 2 = 0 (2) là:

    \sqrt{x + 1} = 2 \Leftrightarrow x + 1 = 4 \Leftrightarrow x = 3

    Do đó, để mọi nghiệm của (1) cũng là nghiệm của (2) điều kiện là x = 3 cũng là nghiệm của (2), tức là: 9 - 6m - m^{2} - 2 = 0 \Leftrightarrow m^{2} + 6m - 7 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = - 7 \\ \end{matrix} ight..

  • Câu 14: Nhận biết

    Cho ba điểm A,\ B,\ C phân biệt. Khi đó:

    Chọn: Điều kiện cần và đủ để A,\ B,\ C thẳng hàng là \overrightarrow{AB} cùng phương với \overrightarrow{AC}.

  • Câu 15: Thông hiểu

    Cho bốn điểm phân biệt A,\ B,\ C,\ Dvà không cùng nằm trên một đường thẳng. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để \overrightarrow{AB} = \overrightarrow{CD}?

    Ta có:

    \overrightarrow{AB} = \overrightarrow{CD} \Rightarrow \left\{ \begin{matrix} AB \parallel CD \\ AB = CD \\ \end{matrix} ight.\ \Rightarrow ABDC là hình bình hành.

    Mặt khác, ABDC là hình bình hành \Rightarrow \left\{ \begin{matrix} AB \parallel CD \\ AB = CD \\ \end{matrix} ight.\ \Rightarrow \overrightarrow{AB} = \overrightarrow{CD}.

    Do đó, điều kiện cần và đủ để \overrightarrow{AB} = \overrightarrow{CD} là ABDC là hình bình hành.

  • Câu 16: Thông hiểu

    Cho f(x)=ax^{2}+bx+c(a≠0)có Δ=b^{2}−4ac<0. Khi đó mệnh đề nào đúng?

     Khi \Delta<0 thì f(x) luôn cùng dấu với hệ số a \text{ } \forall x\in \mathbb{R}. Do đó nó không đổi dấu.

  • Câu 17: Thông hiểu

    Cho hệ bất phương trình \left\{ \begin{matrix}2x - 5y - 1 > 0 \\2x + y + 5 > 0 \\x + y + 1 < 0 \\\end{matrix} ight.. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

    Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

    Với O(0;0) \Rightarrow \left\{\begin{matrix}2.0 - 5.0 - 1 > 0 \\2.0 + 0 + 5 > 0 \\0 + 0 + 1 < 0 \\\end{matrix} ight.. Bất phương trình thứ nhất và thứ ba sai nên không thỏa mãn.

    Với M(1;0) \Rightarrow \left\{\begin{matrix}2.1 - 5.0 - 1 > 0 \\2.1 + 0 + 5 > 0 \\1 + 0 + 1 < 0 \\\end{matrix} ight.. Bất phương trình thứ ba sai nên không thỏa mãn.

    Với N(0; - 3) \Rightarrow \left\{\begin{matrix}2.0 - 5.( - 3) - 1 > 0 \\2.0 + ( - 2) + 5 > 0 \\0 + ( - 2) + 1 < 0 \\\end{matrix} ight.. Đúng.

  • Câu 18: Thông hiểu

    Gọi M,N lần lượt là trung điểm của các cạnh AB và CD của tứ giác ABCD. Mệnh đề nào sau đây đúng?

    Do M là trung điểm các cạnh AB nên \overrightarrow{MB} + \overrightarrow{MA} = \overrightarrow{0}.

    Do N lần lượt là trung điểm các cạnh DC nên 2\overrightarrow{MN} = \overrightarrow{MC} + \overrightarrow{MD}.

    Ta có

    2\overrightarrow{MN} =\overrightarrow{MC} + \overrightarrow{MD}= \overrightarrow{MB} +\overrightarrow{BC} + \overrightarrow{MA} + \overrightarrow{AD}=\overrightarrow{AD} + \overrightarrow{BC} + \left( \overrightarrow{MA} +\overrightarrow{MB} ight) = \overrightarrow{AD} +\overrightarrow{BC}

    Mặt khác \overrightarrow{AC} + \overrightarrow{BD} = \overrightarrow{AC} + \overrightarrow{BC} + \overrightarrow{CD} = \overrightarrow{BC} + \left( \overrightarrow{AC} + \overrightarrow{CD} ight) = \overrightarrow{BC} + \overrightarrow{AD}

    Do đó \overrightarrow{AC} + \overrightarrow{BD} + \overrightarrow{BC} + \overrightarrow{AD} = 4\overrightarrow{MN}.

  • Câu 19: Thông hiểu

    Có bao nhiêu mệnh đề trong các câu sau?

    Hôm nay trời đẹp quá!

    Trung Quốc là nước đông dân nhất thế giới.

    Năm 2018 là năm nhuận.

    Câu “Hôm nay trời đẹp quá!” không phải là mệnh đề. Các câu còn lại đều là mệnh đề.

  • Câu 20: Nhận biết

    Cho hệ bất phương trình \left\{ \begin{matrix} 2x + y - 2 \leq 0 \\ x - 3y + 2 > 0 \\ \end{matrix} ight.. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

    Với O(0;0). Ta có: \left\{ \begin{matrix} 2.0 + 0 - 2 \leq 0 \\ 0 - 3.0 + 2 > 0 \\ \end{matrix} ight. . Cả hai bất phương trình đều thỏa mãn. Chọn đáp án này.

  • Câu 21: Nhận biết

    Hàm số y = 2x2 + 4x − 1

    Hàm số y = ax2 + bx + c với a > 0 đồng biến trên khoảng \left( - \frac{b}{2a}; + \infty ight), nghịch biến trên khoảng \left( - \infty; - \frac{b}{2a} ight).

    Áp dụng: Ta có - \frac{b}{2a} = - 1. Do đó hàm số nghịch biến trên khoảng (−∞;−1) và đồng biến trên khoảng (−1;+∞).

  • Câu 22: Thông hiểu

    Giá trị lớn nhất của hàm số f(x) = \frac{2}{x^{2} - 5x + 9} bằng:

    Ta có x^{2} - 5x + 9 = \left( x - \frac{5}{2} ight)^{2} + \frac{11}{4} \geq \frac{11}{4} \Rightarrow \frac{2}{x^{2} - 5x + 9} \leq \frac{2}{\frac{11}{4}} = \frac{8}{11}

    \frac{2}{x^{2} - 5x + 9} = \frac{8}{11} \Leftrightarrow x = \frac{5}{2}

    Vậy giá trị lớn nhất của hàm số f(x) = \frac{2}{x^{2} - 5x + 9} bằng \frac{8}{11}.

  • Câu 23: Vận dụng cao

    Gia đình bác Tuân dự định trồng cà phê và sầu riêng trên diện tích 8 ha. Nếu trồng cà phê thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng sầu riêng thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lợi nhuận cao nhất biết rằng tổng số công không quá 180?

    Diện tích trồng cà phê là: 6 (ha)

    Diện tích trồng sầu riêng là: 2 (ha)

    Đáp án là:

    Gia đình bác Tuân dự định trồng cà phê và sầu riêng trên diện tích 8 ha. Nếu trồng cà phê thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng sầu riêng thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lợi nhuận cao nhất biết rằng tổng số công không quá 180?

    Diện tích trồng cà phê là: 6 (ha)

    Diện tích trồng sầu riêng là: 2 (ha)

    Gọi diện tích trồng cà phê và sầu riêng mà hộ gia đình này trồng lần lượt là x và y (ha)

    Điều kiện: x,y \geq 0

    Lợi nhuận thu được là f(x;y) = 3000000x + 4000000y (đồng).

    Tổng số công dùng để trồng x ha cà phê và y ha sầu riêng là 20x + 30y.

    Ta có hệ bất phương trình sau: \left\{ \begin{matrix} x + y \leq 8 \\ 20x + 30y \leq 180 \\ x,y \geq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x + y \leq 8 \\ 2x + 3y \leq 18 \\ x,y \geq 0 \\ \end{matrix} ight.\ (*)

    Bài toán trở thành tìm giá trị lớn nhất của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (*)

    Miền nghiệm của hệ bất phương trình (*) là tứ giác OABC (kể cả biên)

    Hình vẽ minh họa

    Hàm số f(x;y) sẽ đạt giá trị lớn nhất khi (x;y) là tọa độ của một trong các đỉnh O(0;0),A(8;0),B(6;2),C(0;6).

    Ta có: \left\{ \begin{matrix} f(0;0) = 0 \\ f(8;0) = 24000000 \\ f(6;2) = 26000000 \\ f(0;6) = 2400000 \\ \end{matrix} ight..

    Suy ra f(x;y) lớn nhất khi (x;y) = (6;2)

    Vậy hộ gia đình này cần phải trồng 6 ha cà phê và 2 ha sầu riêng thì sẽ thu về lợi nhuận lớn nhất.

  • Câu 24: Nhận biết

    Cho tam giác ABC. Gọi Mvà N lần lượt là trung điểm của AB và AC. Khẳng định nào sau đây sai?

    Vì M,\ \ N lần lượt là trung điểm của AB,\ \ AC. Suy ra MN là đường trung bình của tam giác

    ABC\overset{}{ightarrow}MN = \frac{1}{2}BC. Mà \overrightarrow{BC},\ \ \ \overrightarrow{MN} là hai vectơ cùng hướng nên \overrightarrow{BC} = 2\ \overrightarrow{MN}.

  • Câu 25: Nhận biết

    Cho ba điểm A,\ B,\ C phân biệt. Khẳng định nào sau đây đúng?

    Xét đáp án \overrightarrow{MP} + \overrightarrow{NM} = \overrightarrow{NP}. Ta có \overrightarrow{MP} + \overrightarrow{NM} = \overrightarrow{NM} + \overrightarrow{MP} = \overrightarrow{NP}. Vậy đáp án này đúng.

  • Câu 26: Vận dụng cao

    Cho đồ thị hàm số y = f(x) như hình vẽ:

    Có bao nhiêu giá trị nguyên của m để phương trình f^{2}\left( |x| ight) + mf\left( |x| ight) - 4 + 2m = 0 có 8 nghiệm phân biệt?

    Từ đồ thị hàm số y = f(x) ta suy ra đồ thị hàm số y = f\left( |x| ight) có dạng như hình vẽ:

    Ta có:

    f^{2}\left( |x| ight) + mf\left( |x| ight) - 4 + 2m = 0

    \Leftrightarrow \left\lbrack \begin{matrix} f\left( |x| ight) = 2 - m \\ f\left( |x| ight) = - 2 \\ \end{matrix} ight.

    Dựa vào đồ thị hàm số y = f\left( |x| ight) ta có phương trình f\left( |x| ight) = - 2 có 4 nghiệm, phương trình đã cho có 8 nghiệm khi phương trình f\left( |x| ight) = 2 - m có 4 nghiệm và 2 - m eq - 2

    Suy ra \left\{ \begin{matrix} - 3 < 2 - m < 1 \Leftrightarrow 1 < m < 5 \\ 2 - m eq - 2 \Leftrightarrow m eq 4 \\ \end{matrix} ight.

    Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

  • Câu 27: Nhận biết

    Tam giác ABC có AB=5,BC=7,CA=8. Số đo góc \hat A bằng:

     Áp dụng định lí côsin:

    \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}= \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.

    Suy ra \hat A = 60^{\circ}.

  • Câu 28: Vận dụng

    Cho tam giác ABC. Tập hợp các điểm M thỏa mãn \overrightarrow{MA}.(\overrightarrow{MB}+\overrightarrow{MC})=0 là:

    Ta có: \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} (I là trung điểm của BC)

    \begin{matrix} \overrightarrow {MA} .\left( {\overrightarrow {MB} + \overrightarrow {MC} } ight) = 0 \hfill \\ \Leftrightarrow \overrightarrow {MA} .\left( {2\overrightarrow {MI} } ight) = 0 \hfill \\ \Leftrightarrow 2\overrightarrow {MA} .\overrightarrow {MI} = 0 \hfill \\ \Leftrightarrow \overrightarrow {MA} .\overrightarrow {MI} = 0 \hfill \\ \Rightarrow \cos \left( {\overrightarrow {MA} ,\overrightarrow {MI} } ight) = {90^0} \hfill \\ \Leftrightarrow \overrightarrow {MA} \bot \overrightarrow {MI} \hfill \\ \end{matrix}

    \Rightarrow \widehat {AMI} = {90^0}

    => Qũy tích điểm M là đường tròn đường kính IA.

  • Câu 29: Thông hiểu

    Cho tập X = \left\{ 2,3,4 ight\}. Tập X có bao nhiêu tập hợp con?

    Tập X có 3 phần tử \Rightarrow số tập con của X bằng: 2^{3} = 8.

  • Câu 30: Thông hiểu

    Một học sinh dùng giác kế, đứng cách chân cột cờ 10m rồi chỉnh mặt trước cao bằng mắt của mình để xác định góc nâng (góc tạo bởi tia sáng đi thẳng từ đỉnh cột cờ) với mắt tạo với phương nằm ngang. Khi đó góc nâng đo được 31∘. Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng 1,5m. Chiều cao cột cờ gần nhất với giá trị nào?

    Hình vẽ minh họa

    Gọi AB là khoảng cách từ chân đến tầm mắt của học sinh ⇒ AB = 1,5m.

    AC là khoảng cách từ chân đến cột cờ ⇒ AC = 10m.

    CD là chiều cao cột cờ.

    BE là phương ngang của tầm mắt.

    Khi đó góc nâng là \widehat{DBE} = 31^{0}.

    Do ABEC là hình chữ nhật nên \left\{ \begin{matrix} BE = AC = 10m \\ CE = AB = 1,5m \\ \end{matrix} ight..

    Ta có: \tan\widehat{DBE} = \frac{DE}{BE} \Rightarrow DE = 10.tan31^{0} \approx 6m.

    Vậy chiều cao của cột cờ là: CD = CE + DE = 6 + 1,5 = 7,5m.

  • Câu 31: Thông hiểu

    Tam giác ABC có \widehat A = {105^0},\widehat B = {45^0};AC = 10. Độ dài cạnh AB là:

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat A + \widehat B + \widehat C = {180^0} \hfill \\ \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} ight) = {30^0} \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin \widehat B}} = \dfrac{{AB}}{{\sin \widehat C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin \widehat C}}{{\sin \widehat B}} = \dfrac{{10.\sin {{30}^0}}}{{\sin {{45}^0}}} = 5\sqrt 2 \hfill \\ \end{matrix}

  • Câu 32: Thông hiểu

    Số nghiệm của phương trình \sqrt{x + 4} = \sqrt{1 - x} + \sqrt{1 - 2x}  là

    Điều kiện: \left\{ \begin{matrix}x + 4 \geq 0 \\1 - x \geq 0 \\1 - 2x \geq 0 \\\end{matrix} ight.\ \Leftrightarrow - 4 \leq x \leq\frac{1}{2}.

    \sqrt{x + 4} = \sqrt{1 - x} + \sqrt{1 -2x} \Leftrightarrow \sqrt{(1 - x)(1 - 2x)} = 2x + 1

    ⇔ \left\{\begin{matrix}2x + 1 \geq 0 \\(1 - x)(1 - 2x) = (2x + 1)^{2} \\\end{matrix} ight.

    ⇔ \left\{\begin{matrix}x \geq - \frac{1}{2} \\2x^{2} + 7x = 0 \\\end{matrix} ight.

    ⇔ \left\{\begin{matrix}x \geq - 1/2 \\\left\lbrack \begin{matrix}x = 0 \\x = - 7/2 \\\end{matrix} ight.\ \\\end{matrix} ight.  ⇔ x = 0(TM).

    Vậy, phương trình có một nghiệm.

  • Câu 33: Vận dụng cao

    Cho tam giác ABC đều cạnh a. Đường thẳng \Delta qua A và song song với BC, lấy điểm M \in \Delta. Tính giá trị nhỏ nhất của \left| \overrightarrow{CA} + 2\overrightarrow{MB} ight| khi M di động trên \Delta.

    Hình vẽ minh họa

    Kẻ hình bình hành ACBD. Gọi I là trung điểm BD, khi đó, ta có

    Ta có:

    \left| \overrightarrow{CA} + 2\overrightarrow{MB} ight| = \left| \overrightarrow{CA} + 2\left( \overrightarrow{IB} - \overrightarrow{IM} ight) ight|

    = \left| \overrightarrow{CA} + 2\overrightarrow{IB} - 2\overrightarrow{IM} ight| = \left| \overrightarrow{CA} + \overrightarrow{DB} - 2\overrightarrow{IM} ight|

    = \left| \overrightarrow{CA} - \overrightarrow{CA} - 2\overrightarrow{IM} ight|

    = 2\left| \overrightarrow{IM} ight| \geq 2IH = 2.\frac{1}{2}.\frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{2}

    Dấu “=” xảy ra khi và chỉ khi M trùng với điểm H là hình chiếu vuông góc của điểm I trên đường thẳng \Delta.

  • Câu 34: Nhận biết

    Đâu là tập nghiệm của phương trình \sqrt{x^{2} - 2x} = \sqrt{2x - x^{2}}?

    \sqrt{x^{2} - 2x} = \sqrt{2x - x^{2}}\Leftrightarrow \left\{ \begin{matrix}x^{2} - 2x \geq 0 \\x^{2} - 2x = 2x - x^{2} \\\end{matrix} ight.\ \Leftrightarrow x^{2} - 2x = 0 \Leftrightarrow\left\lbrack \begin{matrix}x = 0 \\x = 2 \\\end{matrix} ight..

    Vậy tập nghiệm của phương trình là S = \left\{ 0;2 ight\}.

  • Câu 35: Thông hiểu

    Miền nghiệm của bất phương trình \left( 1 + \sqrt{3} ight)x - \left( 1 - \sqrt{3} ight)y \geq 2 chứa điểm nào sau đây?

    Xét điểm A(1\ \ ;\ \ - 1). Vì \left( 1 + \sqrt{3} ight).1 - \left( 1 - \sqrt{3} ight).( - 1) = 2 \geq 2 nên miền nghiệm của bất phương trình chứa điểm A(1\ \ ;\ \ - 1).

  • Câu 36: Vận dụng

    Tam giác ABC vuông tại A, có AB = c,\ \ AC = b. Gọi \mathcal{l}_{a} là độ dài đoạn phân giác trong góc \widehat{BAC}. Tính \mathcal{l}_{a} theo b và c.

    Ta có BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{b^{2} + c^{2}}

    Do AD là phân giác trong của \widehat{BAC}

    \Rightarrow BD = \frac{AB}{AC}.DC = \frac{c}{b}.DC = \frac{c}{b + c}.BC = \frac{c\sqrt{b^{2} + c^{2}}}{b + c}.

    Theo định lí hàm cosin, ta có

    BD^{2} = AB^{2} + AD^{2} - 2.AB.AD.cos\widehat{ABD} \Leftrightarrow \frac{c^{2}\left( b^{2} + c^{2} ight)}{(b + c)^{2}} = c^{2} + AD^{2} - 2c.AD.cos45{^\circ}

    \Rightarrow AD^{2} - c\sqrt{2}.AD + \left( c^{2} - \frac{c^{2}\left( b^{2} + c^{2} ight)}{(b + c)^{2}} ight) = 0 \Leftrightarrow AD^{2} - c\sqrt{2}.AD + \frac{2bc^{3}}{(b + c)^{2}} = 0.

    \Rightarrow AD = \frac{\sqrt{2}bc}{b + c} hay \mathcal{l}_{a} = \frac{\sqrt{2}bc}{b + c}.

  • Câu 37: Vận dụng

    Cho góc \alpha thỏa mãn \tan\alpha = 2. Tính P = \frac{3sin\alpha - 2cos\alpha}{5cos\alpha + 7sin\alpha}.

    Chia cả tử và mẫu của P cho \cos\alpha ta được P = \frac{3tan\alpha - 2}{5 + 7tan\alpha} = \frac{3.2 - 2}{5 + 7.2} = \frac{4}{19}

  • Câu 38: Nhận biết

    Cho hàm số y =  − x2 + 4x + 1. Khẳng định nào sau đây sai?

    Hàm số y = ax2 + bx + c với a < 0 nghịch biến trên khoảng \left( - \frac{b}{2a}; + \infty ight), đồng biến trên khoảng \left( - \infty; - \frac{b}{2a} ight).

    Áp dụng: Ta có - \frac{b}{2a} = 2. Do đó hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (−∞;2). Do đó Hàm số nghịch biến trên khoảng (4;+∞) và đồng biến trên khoảng (−∞;4) sai. Chọn đáp án này.

    Đáp án Trên khoảng (−∞;−1) hàm số đồng biến đúng vì hàm số đồng biến trên khoảng (−∞;2) thì đồng biến trên khoảng con (−∞;−1).

    Đáp án Trên khoảng (3;+∞) hàm số nghịch biến đúng vì hàm số nghịch biến trên khoảng (2;+∞) thì nghịch biến trên khoảng con (3;+∞).

  • Câu 39: Thông hiểu

    Cho hàm số f(x) = \left\{ \begin{matrix} \frac{2\sqrt{x - 2} - 3}{x - 1} & khi & x \geq 2 \\ x^{2} + 2 & khi & x < 2 \\ \end{matrix} ight.. Tính P = f(2) + f(−2).

    Ta có: f(2) + f( - 2) = \frac{2\sqrt{2 - 2} - 3}{2 - 1} + ( - 2)^{2} + 2 \Rightarrow P = 3.

  • Câu 40: Vận dụng

    Cho điểm A(3;3) và điểm M thuộc miền nghiệm của hệ bất phương trình \left\{ \begin{matrix} x + y - 2 \leq 0 \\ x + y + 2 \geq 0 \\ - x + y + 2 \geq 0 \\ x - y + 2 \geq 0 \\ \end{matrix} ight.. Độ dài AM lớn nhất là

    Miền nghiệm của hệ bất phương trình là miền không bị gạch trong hình bên.

    Suy ra độ dài AM lớn nhất khi và chỉ khi M trùng với đỉnh nào đó của đa giác nghiệm.

    => AM_{max}=\sqrt{34}

  • Câu 41: Nhận biết

    Tìm mệnh đề chứa biến.

    “x + 2 = 11.” là mệnh đề chứa biến.

  • Câu 42: Vận dụng cao

    Cho hình vuông ABCD, dựng các hình vuông A_{1}A_{2}A_{3}A_{4};B_{1}B_{2}B_{3}B_{4};C_{1}C_{2}C_{3}C_{4};D_{1}D_{2}D_{3}D_{4} với A,B,C,D là tâm các hình vuông biểu diễn như hình vẽ dưới đây:

    Biết các hình vuông nhỏ có kích thước 1cm \times 1cm. Tính độ dài vectơ:

    \overrightarrow{A_{1}B_{1}} + \overrightarrow{B_{2}C_{2}} + \overrightarrow{C_{3}D_{3}} + \overrightarrow{D_{4}A_{4}}

    + \overrightarrow{A_{2}B_{2}} + \overrightarrow{B_{3}C_{3}} + \overrightarrow{C_{4}D_{4}} + \overrightarrow{D_{1}A_{1}}

    + \overrightarrow{A_{3}B_{3}} + \overrightarrow{B_{4}C_{4}} + \overrightarrow{C_{1}D_{1}} + \overrightarrow{D_{2}A_{2}}

    Hình vẽ minh họa

    Ta có:

    \overrightarrow{A_{1}B_{1}} + \overrightarrow{B_{2}C_{2}} + \overrightarrow{C_{3}D_{3}} + \overrightarrow{D_{4}A_{4}}

    = \overrightarrow{B_{2}B_{1}} + \overrightarrow{C_{3}C_{2}} + \overrightarrow{D_{2}D_{3}} + \overrightarrow{A_{1}E} + \overrightarrow{EA_{4}} = \overrightarrow{X_{1}Z_{1}}

    \overrightarrow{A_{2}B_{2}} + \overrightarrow{B_{3}C_{3}} + \overrightarrow{C_{4}D_{4}} + \overrightarrow{D_{1}A_{1}}

    = \overrightarrow{B_{3}B_{2}} + \overrightarrow{C_{4}C_{3}} + \overrightarrow{D_{1}D_{4}} + \overrightarrow{A_{2}F} + \overrightarrow{FA_{1}} = \overrightarrow{X_{2}Z_{2}}

    \overrightarrow{A_{3}B_{3}} + \overrightarrow{B_{4}C_{4}} + \overrightarrow{C_{1}D_{1}} + \overrightarrow{D_{2}A_{2}}

    = \overrightarrow{B_{4}B_{3}} + \overrightarrow{C_{1}C_{4}} + \overrightarrow{D_{2}D_{1}} + \overrightarrow{A_{3}K} + \overrightarrow{KA_{2}} = \overrightarrow{X_{3}Z_{3}}

    Khi đó tổng vecto cần tính có kết quả là:

    |\overrightarrow{A_{1}B_{1}} + \overrightarrow{B_{2}C_{2}} + \overrightarrow{C_{3}D_{3}} + \overrightarrow{D_{4}A_{4}}

    + \overrightarrow{A_{2}B_{2}} + \overrightarrow{B_{3}C_{3}} + \overrightarrow{C_{4}D_{4}} + \overrightarrow{D_{1}A_{1}}

    + \overrightarrow{A_{3}B_{3}} + \overrightarrow{B_{4}C_{4}} + \overrightarrow{C_{1}D_{1}} + \overrightarrow{D_{2}A_{2}}|

    = \left| \overrightarrow{X_{1}Z_{1}} + \overrightarrow{X_{2}Z_{2}} + \overrightarrow{X_{3}Z_{3}} ight| = \left| \overrightarrow{MN} + \overrightarrow{MQ} ight| = \left| \overrightarrow{MP} ight| = \sqrt{34}

  • Câu 43: Thông hiểu

    Cho tam giác ABC với M,\ \ N,\ \ P lần lượt là trung điểm của. Khẳng định nào sau đây sai?

    Xét các đáp án:

    Đáp án \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \overrightarrow{0}.. Ta có \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \overrightarrow{AA} = \overrightarrow{0}.

    Đáp án \overrightarrow{AP} + \overrightarrow{BM} + \overrightarrow{CN} = \overrightarrow{0}.. Ta có \overrightarrow{AP} + \overrightarrow{BM} + \overrightarrow{CN} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{BC} + \frac{1}{2}\overrightarrow{CA}

    = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} ight) = \frac{1}{2}\overrightarrow{AA} = \overrightarrow{0}.

    Đáp án \overrightarrow{MN} + \overrightarrow{NP} + \overrightarrow{PM} = \overrightarrow{0}.. Ta có \overrightarrow{MN} + \overrightarrow{NP} + \overrightarrow{PM} = \overrightarrow{MM} = \overrightarrow{0}.

    Đáp án \overrightarrow{PB} + \overrightarrow{MC} = \overrightarrow{MP}.. Ta có \overrightarrow{PB} + \overrightarrow{MC} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{BC} = \frac{1}{2}\overrightarrow{AC} = \overrightarrow{AN} = \overrightarrow{PM} = - \overrightarrow{MP}. Chọn đáp án này.

  • Câu 44: Vận dụng

    Cho parabol (P):y=ax^{2}+bx+c (aeq0). Xét dấu hệ số a và biệt thức \Delta khi (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía trên trục hoành.

     Nhận xét: Đồ thị hàm số bậc hai cắt trục hoành tại 2 điểm phân biệt nên suy ra phương trình y=0 có 2 nghiệm phân biệt. Suy ra \Delta >0.

    Đỉnh nằm phía trên trục hoành nên suy ra a<0 (bề lõm hướng xuống). 

  • Câu 45: Thông hiểu

    Cho hai tập hợp A = ( - 3;5brack,B = \lbrack a; + \infty). Tìm a để A \cap B có đúng một phần tử.

    Để A \cap B có đúng một phần tử khi và chỉ khi a = 5. Khi đó A \cap B = \{ 5\}.

    Vậy a = 5 là giá trị cần tìm.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Cánh Diều Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 9 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 10 Cánh Diều Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập