Cho ![]() với
với ![]() . Tính
. Tính ![]() .
.
Ta có:
.
Do nên
. Suy ra,
Cho ![]() với
với ![]() . Tính
. Tính ![]() .
.
Ta có:
.
Do nên
. Suy ra,
Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?
Đồ thị hàm số bậc hai là một đường parabol có đỉnh là điểm
, có trục đối xứng là đường thẳng
. Parabol này quay bề lõm lên trên nếu
.
Hàm số có
=> Đồ thị hàm số có bề lõm quay lên.
Trên nóc một tòa nhà có một cột ăng-ten cao ![]() . Từ vị trí quan sát
. Từ vị trí quan sát ![]() cao
cao ![]() so với mặt đất, có thể nhìn thấy đỉnh
so với mặt đất, có thể nhìn thấy đỉnh ![]() và chân
và chân ![]() của cột ăng-ten dưới góc
của cột ăng-ten dưới góc ![]() và
và ![]() so với phương nằm ngang.
so với phương nằm ngang.
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

Từ hình vẽ, suy ra và
.
Áp dụng định lí sin trong tam giác , ta có
.Trong tam giác vuông
, ta có
Vậy
Cho hai điểm cố định ![]() ; gọi
; gọi ![]() là trung điểm
là trung điểm ![]() . Tập hợp các điểm
. Tập hợp các điểm ![]() thoả:
thoả: ![]() là:
là:
Ta có
Vậy tập hợp các điểm là đường tròn đường kính
.
Tam giác ABC có ![]() . Độ dài cạnh AB là:
. Độ dài cạnh AB là:
Xét tam giác ABC ta có:
Áp dụng định lí sin cho tam giác ABC ta có:
Tất cả các giá trị của tham số m để phương trình ![]() có nghiệm là:
có nghiệm là:
ĐKXĐ: x ≥ 1 .
Chia cả hai vế cho ta có
Đặt
Phương trình trở thành − 3t2 + 2t = m (*)
Xét hàm số y = − 3t2 + 2t trên [0; 1) , ta có ,
Bảng biến thiên
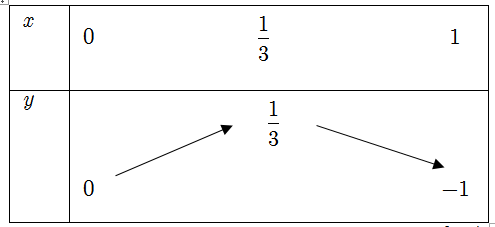
Phương trình ban đầu có nghiệm ⇔ phương trình (*) có nghiệm t∈ [0; 1)
⇔ đồ thị hàm số y = − 3t2 + 2t trên [0; 1) cắt đường thẳng
Vậy phương trình ban đầu có nghiệm khi và chỉ khi .
Cho ba điểm phân biệt ![]() Có bao nhiêu vectơ khác vectơ không có điểm đầu và điểm cuối là các điểm
Có bao nhiêu vectơ khác vectơ không có điểm đầu và điểm cuối là các điểm ![]() đã cho?
đã cho?
Các vectơ khác vectơ không có điểm đầu và điểm cuối là các điểm đã cho là
.
Tam giác ![]() có
có ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Theo định lí hàm cosin, ta có
.
Hãy chọn kết quả đúng khi phân tích vectơ ![]() theo hai vectơ
theo hai vectơ ![]() và
và ![]() của tam giác
của tam giác ![]() với trung tuyến
với trung tuyến ![]() .
.
Do là trung điểm của
nên ta có
.
Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng ![]() là:
là:
Ta có:
Cho hệ bất phương trình  . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.
Với . Bất phương trình thứ nhất sai nên không thỏa mãn.
Với . Bất phương trình thứ ba sai nên không thỏa mãn.
Với . Đúng. Chọn đáp án này.
Cho 4 điểm ![]() phân biệt. Khi đó
phân biệt. Khi đó ![]() bằng
bằng
.
Miền nghiệm của bất phương trình ![]() không chứa điểm nào sau đây?
không chứa điểm nào sau đây?
Xét điểm . Ta có:
nên miền nghiệm của bất phương trình trên không chứa điểm
.
Điểm ![]() thuộc miền nghiệm của hệ bất phương trình nào sau đây?
thuộc miền nghiệm của hệ bất phương trình nào sau đây?
Thay tọa độ lần lượt vào từng phương trình của hệ
ta thấy thỏa mãn.
Cho ![]() . Tập A có bao nhiêu tập con có 2 phần tử?
. Tập A có bao nhiêu tập con có 2 phần tử?
Tập con có phần tử của
là:
có
tập con có
phần tử.
Giá trị ![]() thoả mãn
thoả mãn ![]() gần nhất với giá trị:
gần nhất với giá trị:
Để tìm α khi biết tanα = 1,607 thì ta sử dụng máy tính cầm tay và tính được: α ≈ 58°.
Vậy α ≈ 58°
Cho tam thức bậc hai ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có:
Tổng các nghiệm của phương trình ![]() là bao nhiêu?
là bao nhiêu?
.
Vậy tổng các nghiệm của phương trình là .
Cho 2 vectơ ![]() và
và ![]() có
có ![]() ,
, ![]() và
và ![]() . Tính
. Tính ![]() .
.
Ta có
.
Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?
Hình vẽ minh họa
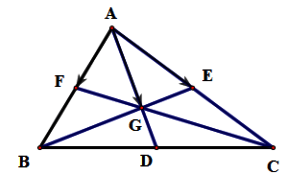
Ta có:
G là trọng tâm tam giác ABC =>
D là trung điểm của BC =>
E là trung điểm của AC =>
F là trung điểm của AB =>
Khi đó:
Mệnh đề nào sau đây là đúng?
nhưng
sai.
nhưng
sai.
nhưng
sai.
Giá trị nhỏ nhất ![]() của biểu thức
của biểu thức ![]() trên miền xác định bởi hệ
trên miền xác định bởi hệ  là :
là :
Trong mặt phẳng tọa độ vẽ các đường thẳng
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
Ta có
Cho tứ giác ![]() Gọi
Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]()
![]()
![]()
![]() Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
Ta có (do cùng song song và bằng
).
Do đó là hình bình hành.
Do đó sai.
Trong hệ trục tọa độ ![]() , tọa độ của vectơ
, tọa độ của vectơ ![]() là
là
Ta có
Cho hình vuông ![]() cạnh
cạnh ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() , lấy các điểm
, lấy các điểm ![]() lần lượt là các điểm thay đổi trên các cạnh
lần lượt là các điểm thay đổi trên các cạnh ![]() sao cho
sao cho ![]() . Tìm giá trị nhỏ nhất của biểu thức
. Tìm giá trị nhỏ nhất của biểu thức ![]() .
.
Hình vẽ minh họa
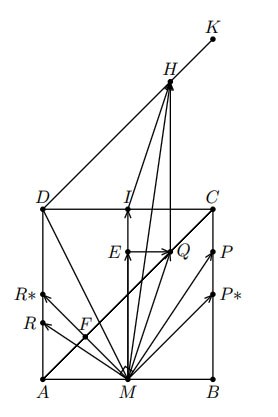
Đặt
Khi đó
Dấu bằng xảy ra khi và chỉ khi hay P, Q là trung điểm của BC, DA
Ta có:
Khi P ≡ P∗, R ≡ R∗, Q thay đổi trên AC, H sẽ thay đổi trên đoạn thẳng DK sao cho tam giác DCK vuông cân tại C.
Ta lại có:
Tam giác ABC có BC = 10 và ![]() . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Ta có: .
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol . Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất , người ta thả một sợi dây chạm đất . Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xáHãy tính độ cao của cổng Arch. (làm tròn kết quả đến hàng phần mười)
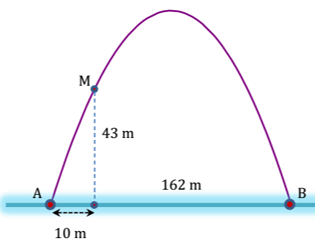
hệ trục tọa độ Oxy như hình vẽ. Phương trình Parabol (P) có dạng y = ax2 + bx + c.
Parabol (P)đi qua điểm A(0;0), B(162;0), M(10;43) nên ta có
.
Do đó chiều cao của cổng là m.
Cho tam giác ![]() thỏa mãn:
thỏa mãn: ![]() . Khi đó:
. Khi đó:
Ta có:
Tìm ![]() để hàm số
để hàm số ![]() luôn đồng biến biến trên tập số thực.
luôn đồng biến biến trên tập số thực.
Để hàm số nghịch biến trên tập số thực thì
.
Tích vô hướng của hai vecto ![]() và
và ![]() là:
là:
Ta có:
Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–2; 3). Gọi B’ là điểm đối xứng của B qua A. Tọa độ điểm B’ là:
Vì B' đối xứng với B qua A => A là trung điểm của BB'
Cho phương trình ![]() với
với ![]() là tham số. Có bao nhiêu giá trị nguyên của tham số
là tham số. Có bao nhiêu giá trị nguyên của tham số ![]() để phương trình đã cho có hai nghiệm trái dấu?
để phương trình đã cho có hai nghiệm trái dấu?
Từ yêu cầu bài toán
Suy ra
Vậy có 20 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Phương trình (m−1)x2 − 2x + m + 1 = 0 có hai nghiệm phân biệt khi
Yêu cầu bài toán
Vậy phương trình có hai nghiệm phân biệt
Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây đúng?
Ta có:
=> Khẳng định sai
=> Khẳng định sai
=> Khẳng định đúng
=> Khẳng định sa
Đồ thị hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?
Nhận xét:
Parabol có bề lõm hường lên.
Parabol cắt trục hoành tại điểm (1;0). Xét các đáp án, đáp án y = 2x2 − 3x + 1. thỏa mãn.
Tìm mệnh đề đúng.
Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Chọn Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
Cho tam giác ![]() có các góc thỏa mãn biểu thức
có các góc thỏa mãn biểu thức
![]()
Giả sử ![]() . Tính số đo góc
. Tính số đo góc ![]() ?
?
Ta có:
Theo định lí cosin ta có:
Ta thấy
Mặt khác
Do đó: khi
Vậy tam giác ABC là tam giác vuông tại .
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Ta có: là bất phương trình bậc nhất hai ẩn.
Cho hàm số: ![]() . Tìm x để
. Tìm x để ![]()
Ta có:
Vậy x = 3 hoặc x = 0
Một nhà máy gồm hai đội công nhân (đội 1 và đội 2) sản xuất nhôm và sắt. Muốn sản xuất một tấn nhôm thì đội 1 phải làm việc trong 3 giờ và đội 2 làm việc trong 1 giờ. Một đội không thể sản xuất đồng thời nhôm và sắt. Đội 1 làm việc không quá 6 giờ một ngày, đội 2 làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà nhà mhà máy thu về trong một ngày là bao nhiêu? Biết một tấn nhôm lãi 2 000 000 đồng, một tấn sắt lãi 1 600 000 triệu đồng.
Gọi x, y lần lượt là số tấn nhôm và sắt mà nhà máy này sản xuất trong một ngày
Điều kiện: x, y > 0
Khi đó số tiền lãi một ngày của nhà máy này là (triệu đồng)
Số giờ làm việc trong ngày của đội 1 là (giờ)
Số giờ làm việc trong ngày của đội 2 là (giờ)
Vì mỗi ngày đội 1 làm việc không quá 6 giờ và đội 2 làm việc không quá 4 giờ nên ta có hệ bất phương trình:
Bài toán trở thành tìm giá trị lớn nhất của hàm số trên miền nghiệm của hệ bất phương trình (∗).
Miền nghiệm của hệ bất phương trình (∗) là tứ giác OABC (kể cả biên).
Hình vẽ minh họa
Hàm số sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (∗) khi
là toạ độ một trong các đỉnh
.
Ta có:
Suy ra khi
Vậy số tiền lãi lớn nhất mà nhà máy thu được trong một ngày là: triệu đồng.
Cho hệ bất phương trình![]() có tập nghiệm
có tập nghiệm ![]() . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
Ta có: . Do đó không có điểm nào thỏa mãn hệ phương trình.
Hệ này vô nghiệm.
Cho mệnh đề ![]() “
“![]() ”. Mệnh đề phủ định của
”. Mệnh đề phủ định của ![]() là:
là:
Phủ định của là
.
Phủ định của là
.
Mệnh đề phủ định của :
.
Tam thức bậc hai f(x) = − x2 − 1 nhận giá trị âm khi và chỉ khi
f(x) = − x2 − 1 = 0 vô nghiệm
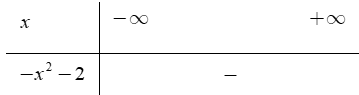
Dựa vào bảng xét dấu, ta chọn đáp án x ∈ ℝ.
Biết ![]() và
và ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Ta có: .
Suy ra và
ngược hướng.
Phương trình ![]() có bao nhiêu nghiệm
có bao nhiêu nghiệm
Đkxđ: .
.
Vậy phương trình có hai nghiệm.
