Cho tam giác ![]() , gọi
, gọi ![]() là trung điểm của
là trung điểm của ![]() và
và ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Do là trung điểm của
nên ta có:
.
Cho tam giác ![]() , gọi
, gọi ![]() là trung điểm của
là trung điểm của ![]() và
và ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Do là trung điểm của
nên ta có:
.
Trong hệ trục tọa độ ![]() , tọa độ của vectơ
, tọa độ của vectơ ![]() là
là
Ta có
Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào ![]() là
là ![]() , chiều dài của hàng rào
, chiều dài của hàng rào ![]() là
là ![]() . Góc giữa hai hàng rào
. Góc giữa hai hàng rào ![]() và
và ![]() là
là ![]() (như hình vẽ).
(như hình vẽ).

Chiều dài hàng rào ![]() là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Áp dụng định li côsin ta
.
Suy ra .
Vậy chiều dài hàng rào là khoảng
.
Các giá trị m để tam thức ![]() đổi dấu 2 lần là:
đổi dấu 2 lần là:
Để đổi dấu 2 lần thì
.
Ta có:
hoặc
.
Cho hai vectơ ![]() và
và ![]() khác
khác ![]() . Xác định góc
. Xác định góc ![]() giữa hai vectơ
giữa hai vectơ ![]() và
và ![]() khi
khi ![]() .
.
Ta có .
Mà theo giả thiết
Suy ra
Cho hàm số có đồ thị như hình vẽ
Khẳng định nào sau đây đúng:
Hàm số đồng biến trên khoảng (1;3).
Cho hàm số: ![]() . Tìm x để
. Tìm x để ![]()
Ta có:
Vậy x = 3 hoặc x = 0
Tìm tất cả các giá trị của m để bất phương trình ![]() với mọi x ∈ ℝ
với mọi x ∈ ℝ
Để bất phương trình với mọi x ∈ ℝ thì:
Trong mặt phẳng tọa độ ![]() , cho tọa độ hai điểm
, cho tọa độ hai điểm ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() đối xứng với điểm
đối xứng với điểm ![]() qua
qua ![]() ?
?
Gọi tọa độ điểm C là
Vì điểm đối xứng với điểm
qua
suy ra
là trung điểm của
Vậy tọa độ điểm C cần tìm là .
Cho ![]() là số tự nhiên, mệnh đề nào sau đây đúng?
là số tự nhiên, mệnh đề nào sau đây đúng?
Với thì
là hai số tự nhiên liên tiếp
là số chẵn
Với thì
là ba số tự nhiên liên tiếp
trong 3 số
có 1 số chia hết cho
Chọn đáp án là số chia hết cho
Cặp số nào sau đây là nghiệm của bất phương trình ![]() ?
?
Xét đáp án (0; 3) ta có: x = 0; y = 3 thay vào bất phương trình ta được:
Vậy (0;3) không là cặp nghiệm của bất phương trình
Xét đáp án (6; 1) ta có: x = 6; y = 1 thay vào bất phương trình ta được:
Vậy (6; 1) là cặp nghiệm của bất phương trình.
Xét đáp án (2; 4) ta có: x = 2; y = 4 thay vào bất phương trình ta được:
Vậy (2; 4) không là cặp nghiệm của bất phương trình.
Xét đáp án (3; 2) ta có: x = 3; y = 2 thay vào bất phương trình ta được:
Vậy (3; 2) không là cặp nghiệm của bất phương trình.
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() và
và ![]() Tính độ dài của
Tính độ dài của ![]()
Ta có
Gọi là trung điểm
Khi đó
Cho tam giác ![]() có diện tích
có diện tích ![]() , lấy
, lấy ![]() là trọng tâm và
là trọng tâm và ![]() . Giả sử
. Giả sử ![]() , tính giá trị biểu thức
, tính giá trị biểu thức ![]() theo
theo ![]() ?
?
Hình vẽ minh họa
Gọi là trung điểm cạnh
. Kẻ
Tam giác vuông =>
Tam giác vuông =>
Ta có:
Mặt khác áp dụng định lí sin cho tam giác AMB ta được:
Từ (*) và (**) ta được:
Chứng minh tương tự ta có:
Do đó:
Tam giác ![]() có đoạn thẳng nối trung điểm của
có đoạn thẳng nối trung điểm của ![]() và
và ![]() bằng
bằng ![]() , cạnh
, cạnh ![]() và
và ![]() . Tính độ dài cạnh cạnh
. Tính độ dài cạnh cạnh ![]() .
.
Gọi lần lượt là trung điểm của
.
là đường trung bình của
.
. Mà
, suy ra
.
Theo định lí hàm cosin, ta có:
Miền nghiệm của bất phương trình ![]() là nửa mặt phẳng không chứa điểm nào trong các điểm sau?
là nửa mặt phẳng không chứa điểm nào trong các điểm sau?
Ta có .
Vì là mệnh đề sai nên
không thuộc miền nghiệm của bất phương trình.
Tập nghiệm của phương trình ![]() là:
là:
Xét phương trình: (1)
Điều kiện :
Thay x = 8 ta thấy (1) thoả mãn. Vậy, phương trình (1) có tập nghiệm là S = {8}.
Miền nghiệm của bất phương trình ![]() chứa điểm nào dưới đây?
chứa điểm nào dưới đây?
Xét điểm . Ta có:
thỏa mãn. Do đó miền nghiệm của bất phương trình
chứa điểm
.
Tập nghiệm của bất phương trình ![]() là:
là:
Tam thức có hai nghiệm phân biệt
a = 2 > 0 nên f(x) dương với mọi x thuộc hai nửa khoảng
Vậy tập nghiệm của bất phương trình là:
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
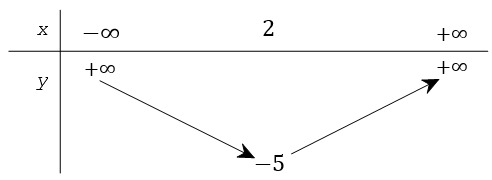
Nhận xét:
Bảng biến thiên có bề lõm hướng lên. Loại đáp án y = − x2 + 4x − 9 và y = − x2 + 4x.
Đỉnh của parabol có tọa độ là (2;−5). Xét các đáp án, đáp án y = x2 − 4x − 1 thỏa mãn.
Xét tính đồng biến, nghịch biến của hàm số f(x) = x2 − 4x + 5 trên các khoảng (−∞; 2) và (2; +∞). Khẳng định nào sau đây đúng?
Xét f(x) = x2 − 4x + 5.
TXĐ: D = ℝ.
Tọa độ đỉnh I(2; 1).
Hàm số nghịch biến trên (−∞; 2), đồng biến trên (2; +∞).
Tìm điểm M(a;b) với a < 0 nằm trên Δ : x + y − 1 = 0 và cách N(−1;3) một khoảng bằng 5. Giá trị của a − b là
.
Ta có: MN = 5 ⇒ MN2 = (−1−t)2 + (2+t)2 = 25
⇔ 2t2 + 6t − 20 = 0
⇒ M(−5;6) ⇒ a − b = − 11
Cho ![]() . Điểm
. Điểm ![]() trên trục
trên trục ![]() sao cho ba điểm
sao cho ba điểm ![]() thẳng hàng thì tọa độ điểm
thẳng hàng thì tọa độ điểm ![]() là:
là:
Ta có: trên trục
.
Ba điểm thẳng hàng khi
cùng phương với
.
Ta có . Do đó,
cùng phương với
. Vậy
.Đáp án là
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x4 − 4x3 − x2 + 10x − 3 trên đoạn [ − 1; 4] là
Ta có y = x4 − 4x3 − x2 + 10x − 3 = x4 − 4x3 + 4x2 − 5x2 + 10x − 5 + 2
= (x2−2x)2 − 5(x−1)2 + 2 = [(x−1)2−1]2 − 5(x−1)2 + 2.
Đặt t = (x−1)2, x ∈ [ − 1; 4] ⇒ t ∈ [0; 9].
.
Cách 1: Ta có .
Cách 2: Vẽ BBT
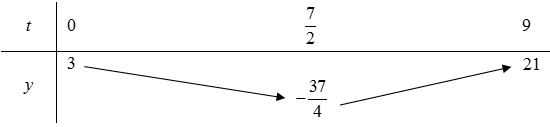
Vậy , ymax = 21.
Miền nghiệm của hệ bất phương trình  chứa điểm nào trong các điểm sau đây?
chứa điểm nào trong các điểm sau đây?
Thay lần lượt tọa độ các điểm vào hệ bất phương trình. Ta thấy điểm thỏa mãn cả 4 phươn trình trong hệ.
Tìm mệnh đề đúng.
Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. là mệnh đề sai: Ví dụ: là số chẵn nhưng
là số lẻ.
Chọn Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
Gia đình bác Tuân dự định trồng cà phê và sầu riêng trên diện tích 8 ha. Nếu trồng cà phê thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng sầu riêng thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lợi nhuận cao nhất biết rằng tổng số công không quá 180?
Diện tích trồng cà phê là: 6 (ha)
Diện tích trồng sầu riêng là: 2 (ha)
Gia đình bác Tuân dự định trồng cà phê và sầu riêng trên diện tích 8 ha. Nếu trồng cà phê thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng sầu riêng thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lợi nhuận cao nhất biết rằng tổng số công không quá 180?
Diện tích trồng cà phê là: 6 (ha)
Diện tích trồng sầu riêng là: 2 (ha)
Gọi diện tích trồng cà phê và sầu riêng mà hộ gia đình này trồng lần lượt là và
(ha)
Điều kiện:
Lợi nhuận thu được là (đồng).
Tổng số công dùng để trồng ha cà phê và
ha sầu riêng là
.
Ta có hệ bất phương trình sau:
Bài toán trở thành tìm giá trị lớn nhất của hàm số trên miền nghiệm của hệ bất phương trình
Miền nghiệm của hệ bất phương trình là tứ giác
(kể cả biên)
Hình vẽ minh họa
Hàm số sẽ đạt giá trị lớn nhất khi
là tọa độ của một trong các đỉnh
.
Ta có: .
Suy ra lớn nhất khi
Vậy hộ gia đình này cần phải trồng 6 ha cà phê và 2 ha sầu riêng thì sẽ thu về lợi nhuận lớn nhất.
Điểm cuối của ![]() thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
Điểm cuối của thuộc góc phần tư thứ hai
.
Trong các cặp số sau, cặp số nào không là nghiệm của hệ bất phương trình ![]()
Thay cặp số vào hệ ta được
không thỏa mãn bất phương trình ở dưới. Do đó cặp số này không là nghiêm của hệ.
Trên mặt phẳng tọa độ Oxy, cho các điểm ![]() . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
Biểu diễn các điểm trên hệ trục tọa độ như sau:
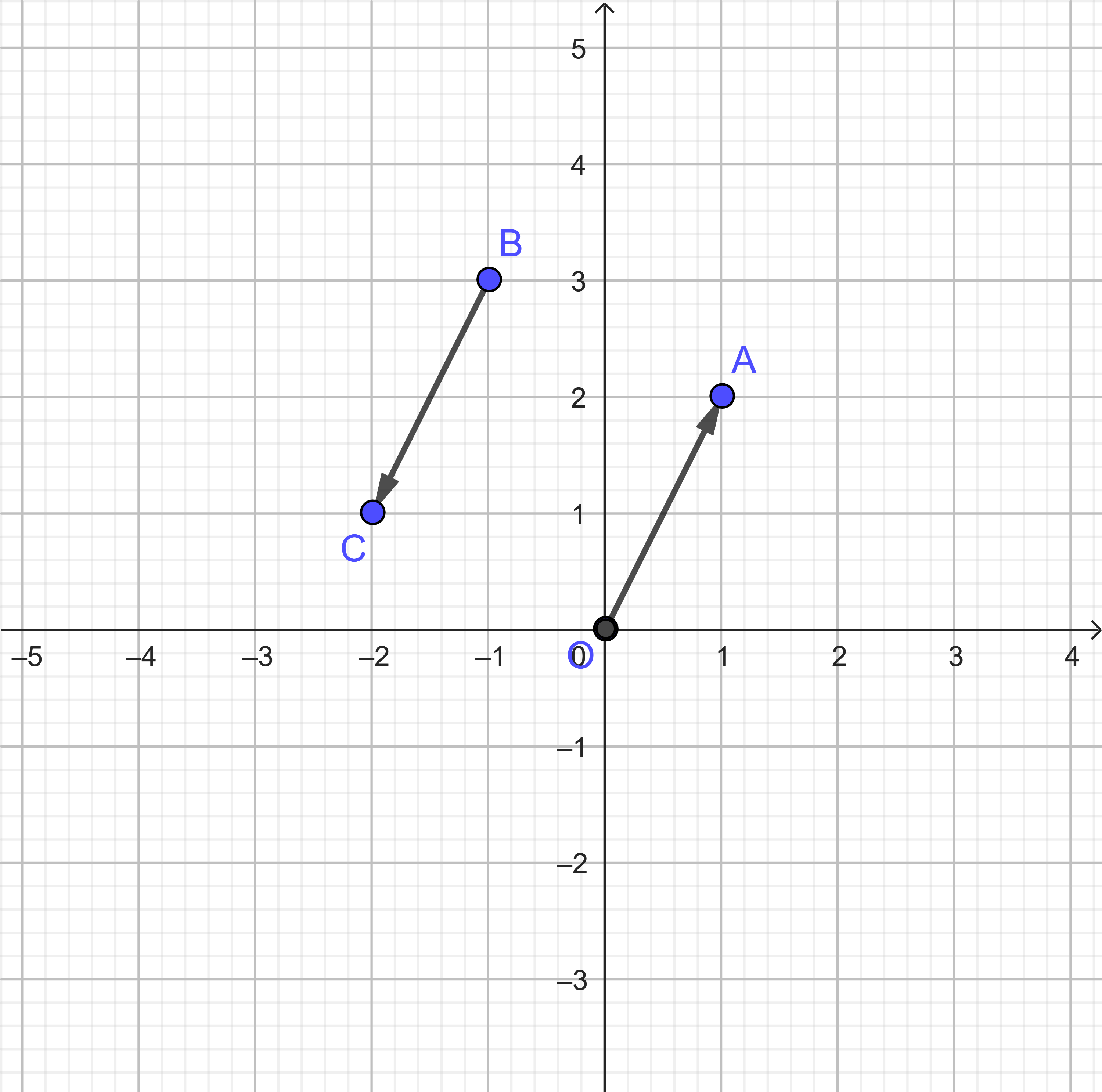
Ta có:
Vậy hai vectơ cùng phương, ngược hướng.
Cho tam giác ![]() có
có ![]() thỏa mãn điều kiện
thỏa mãn điều kiện ![]() . Xác định vị trí điểm
. Xác định vị trí điểm ![]()
Gọi là trọng tâm tam giác
.
Ta có .
Cho ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có . Do đó:
và
ngược hướng.
và
cùng độ dài.
là hình bình hành nếu
và
không cùng giá.
Chọn đáp án và
cùng độ dài.
Cho bốn điểm phân biệt ![]() thỏa mãn
thỏa mãn ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Phải suy ra là hình bình hành (nếu
không thẳng hàng) hoặc bốn điểm
thẳng hàng.
Đáp án sai là là hình bình hành.
Cho tọa độ ba điểm ![]() . Tính
. Tính ![]() ?
?
Ta có:
Cho hình bình hành ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Ta có:
sai do
.
sai do
.
sai do
.
đúng do
.
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() cạnh
cạnh ![]() Tính
Tính ![]()
Gọi là điểm đối xứng của
qua
Tam giác
vuông tại
có
Ta có suy ra
Tam giác ![]() có
có ![]() . Số đo góc
. Số đo góc ![]() bằng:
bằng:
Theo định lí hàm cosin, ta có
.
Do đó, .
Cho biết ![]() . Tính
. Tính ![]() .
.
Ta có:
.
Trong các tập hợp sau đây, tập hợp nào bằng tập hợp ![]() :
:
Ta có:
Tập hợp là tập hợp
.
Vậy tập hợp
Cho hai điểm ![]() phân biệt. Tập hợp những điểm
phân biệt. Tập hợp những điểm ![]() thỏa mãn
thỏa mãn ![]() là
là
Ta có:
.
Tập hợp điểm là đường tròn đường kính
.
Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “7 là một số tự nhiên”:
Ta có:
Trong mặt phẳng ![]() cho
cho ![]() . Tích vô hướng của 2 vectơ
. Tích vô hướng của 2 vectơ ![]() là:
là:
Ta có , suy ra
.
Cho hình bình hành ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Do là hình bình hành nên
Suy ra
Hãy liệt kê các phần tử của tập hợp ![]()
Ta có: không có nghiệm thực.
Nghiệm của phương trình  là:
là:
Điều kiện: .
Ta có: .
Loại . Do đó
.
Tập nghiệm của bất phương trình: ![]() là:
là:
Ta có: .
Vậy .
