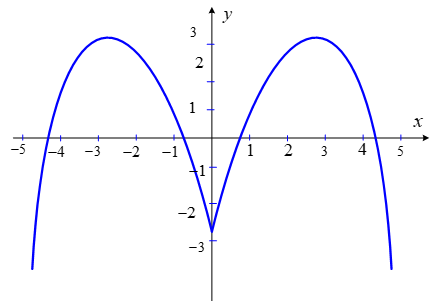
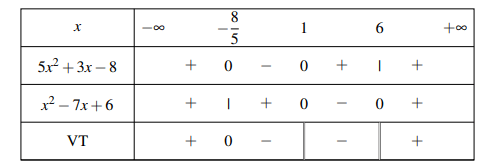Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3

Mô tả thêm: Đề thi học kì 1 Toán 10 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức Toán 10 Chân trời sáng tạo.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Trong các khẳng định sau, khẳng định nào là đúng?

     Ta có: \cos 121^{\circ} =\cos -121^{\circ} vì \cos \alpha =\cos -\alpha.

  • Câu 2: Nhận biết

    Cho \overrightarrow{a} e\overrightarrow{0} và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn \overrightarrow{OM}=3\overrightarrow{a} và \overrightarrow{ON}=-4\overrightarrow{a}. Tìm \overrightarrow{MN}.

    Ta có:

    \begin{matrix} \overrightarrow {MN} = \overrightarrow {MO} + \overrightarrow {ON} \hfill \\ \Rightarrow \overrightarrow {MN} = - \overrightarrow {OM} + \overrightarrow {ON} \hfill \\ \Rightarrow \overrightarrow {MN} = - 3\overrightarrow a + \left( { - 4\overrightarrow a } ight) \hfill \\ \Rightarrow \overrightarrow {MN} = - 3\overrightarrow a - 4\overrightarrow a = 7\overrightarrow a \hfill \\ \end{matrix}

  • Câu 3: Vận dụng

    Cho hàm số y = f(x) = ax2 + bx + c. Biểu thức f(x+3) − 3f(x+2) + 3f(x+1) có giá trị bằng

    f(x+3) = a(x+3)2 + b(x+3) + c = ax2 + (6a+b)x + 9a + 3b + c.

    f(x+2) = a(x+2)2 + b(x+2) + c = ax2 + (4a+b)x + 4a + 2b + c.

    f(x+1) = a(x+1)2 + b(x+1) + c = ax2 + (2a+b)x + a + b + c.

     ⇒ f(x+3) − 3f(x+2) + 3f(x+1) = ax2 + bx + c.

  • Câu 4: Nhận biết

    Cho ba điểm A,\ B,\ C phân biệt. Khẳng định nào sau đây đúng?

    Xét đáp án \overrightarrow{MP} + \overrightarrow{NM} = \overrightarrow{NP}. Ta có \overrightarrow{MP} + \overrightarrow{NM} = \overrightarrow{NM} + \overrightarrow{MP} = \overrightarrow{NP}. Vậy đáp án này đúng.

  • Câu 5: Nhận biết

    Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:

    Điều kiện để I là trung điểm AB là: \overrightarrow{IA} = - \overrightarrow{IB}.

  • Câu 6: Thông hiểu

    Miền nghiệm của hệ bất phương trình \left\{ \begin{matrix} \frac{x}{2} + \frac{y}{3} - 1 \geq 0 \\ x \geq 0 \\ x + \frac{1}{2} - \frac{3y}{2} \leq 2 \\ \end{matrix} ight. chứa điểm nào trong các điểm sau đây?

    Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

    Với O(0;0) \Rightarrow \left\{ \begin{matrix} \frac{0}{2} + \frac{0}{3} - 1 \geq 0 \\ 0 \geq 0 \\ 0 + \frac{1}{2} - \frac{3.0}{2} \leq 2 \\ \end{matrix} ight.. Bất phương trình thứ nhất sai nên không thỏa mãn.

    Với M(2;1) \Rightarrow \left\{ \begin{matrix} \frac{2}{2} + \frac{1}{3} - 1 \geq 0 \\ 2 \geq 0 \\ 2 + \frac{1}{2} - \frac{3.1}{2} \leq 2 \\ \end{matrix} ight.. Đúng.

  • Câu 7: Nhận biết

    Tam thức bậc hai f(x) = x^{2} + \left( 1 - \sqrt{3} ight)x - 8 - 5\sqrt{3}:

    f(x) = x^{2} + \left( 1 - \sqrt{3} ight)x - 8 - 5\sqrt{3} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 - \sqrt{3} \\ x = 1 + 2\sqrt{3} \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, chọn đáp án Âm với mọi x \in \left( - 2 - \sqrt{3};1 + 2\sqrt{3} ight).

  • Câu 8: Vận dụng cao

    Phương trình 2\left( x^{2} - 3x + 2 ight) = 3\sqrt{x^{3} + 8} có mấy nghiệm nguyên ?

    Điều kiện: x ≥  − 2

    PT đã cho tương đương với: 2\left( x^{2} - 2x + 4 ight) - 2(x + 2) = 3\sqrt{(x + 2)\left( x^{2} - 2x + 4 ight)}

    Do x =  − 2 không là nghiệm của PT đã cho nên chia hai vế cho x + 2 ta được:

    \frac{2\left( x^{2} - 2x + 4 ight)}{x + 2} - 3\sqrt{\frac{x^{2} - 2x + 4}{x + 2}} - 2 = 0

    Đặt t = \sqrt{\frac{x^{2} - 2x + 4}{x + 2}}\ \ \ \ (t \geq 0) ta có: 2t^{2} - 3t - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 2\ \ \ (t/m) \\ t = - \frac{1}{2}\ \ \ \ (l) \\ \end{matrix} ight.

    Với t = 2 ta được

    \begin{matrix} \sqrt{\frac{x^{2} - 2x + 4}{x + 2}} = 2 \Leftrightarrow \frac{x^{2} - 2x + 4}{x + 2} = 4 \\ \Leftrightarrow x^{2} - 6x - 4 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 + \sqrt{13} \\ x = 3 - \sqrt{13} \\ \end{matrix} ight.\ (TM) \\ \end{matrix}

    Vậy phương trình có 0 nghiệm nguyên.

  • Câu 9: Nhận biết

    Tìm mệnh đề đúng.

    Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1,\ 3 là số lẻ.

    Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn. là mệnh đề sai: Ví dụ: 2.3 = 6 là số chẵn nhưng 3 là số lẻ.

    Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1,3 là số lẻ.

    Chọn Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

  • Câu 10: Thông hiểu

    Tập nghiệm S của bất phương trình 5(x+1)−x(7−x)>−2x là:

     Ta có: 5(x+1)−x(7−x)>−2x \Leftrightarrow x^2+5>0 (hiển nhiên).

    Vậy S = \mathbb{R}.

  • Câu 11: Thông hiểu

    Biết phương trình \sqrt{x^{2} - 3x + 3} + \sqrt{x^{2} - 3x + 6} =3 có hai nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây là đúng?

    Đặt t = x2 − 3x + 3, ta có: t = \left( x - \frac{3}{2} ight)^{2}+ \frac{3}{4} \geq \frac{3}{4}.

    Do đó điều kiện cho ẩn phụ t là t \geq \frac{3}{4}.

    Khi đó phương trình trở thành:

    \sqrt{t} + \sqrt{t + 3} = 3\Leftrightarrow t + t + 3 +2\sqrt{t(t + 3)} = 9 ⇔ \sqrt{t(t + 3)} = 3 - t

    \Leftrightarrow \left\{ \begin{matrix}3 - t \geq 0 \\t(t + 3) = (3 - t)^{2} \\\end{matrix} ight. ⇔ \left\{ \begin{matrix}t \leq 3 \\t = 1 \\\end{matrix} ight.  ⇔ t = 1(thỏa mãn)

     ⇒ x2 − 3x + 3 = 1⇔ \left\lbrack \begin{matrix}x = 1 = x_{1} \\x = 2 = x_{2} \\\end{matrix} ight.\ \Rightarrow 2x_{1} = x_{2}.

  • Câu 12: Thông hiểu

    Một tam giác có ba cạnh là 52,\ 56,\ 60. Bán kính đường tròn ngoại tiếp tam giác đó là:

    Ta có: p = \frac{52 + 56 + 60}{2} = 84.

    Áp dụng hệ thức Hê - rông ta có:

    S = \sqrt{84 \cdot (84 - 52) \cdot (84 - 56) \cdot (84 - 60)} = 1344.

    Mặt khác S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S\ } = \frac{52.56.60}{4.1344} = 32.5

  • Câu 13: Vận dụng

    Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; - \ 1) và B(3;2). Tìm M thuộc trục tung sao cho MA^{2} + MB^{2} nhỏ nhất.

    Vì M \in Oy \Rightarrow M(0;b).

    Ta có: \overrightarrow{MA} = (1; - 1 - b) \Rightarrow \left| \overrightarrow{MA} ight| = \sqrt{1^{2} + ( - 1 - b)^{2}}

    Ta có: \overrightarrow{MB} = (3;2 - b) \Rightarrow \left| \overrightarrow{MB} ight| = \sqrt{3^{2} + (2 - b)^{2}}

    MA^{2} + MB^{2} = 1 + 1 + 2b + b^{2} + 9 + 4 - 4b + b^{2} = 2b^{2} - 2b + 15 = 2\left\lbrack \left( b - \frac{1}{2} ight)^{2} + \frac{29}{4} ightbrack \geq \frac{29}{2}

    Suy ra MA^{2} + MB^{2} nhỏ nhất khi và chỉ khi b = \frac{1}{2} \Rightarrow M\left( 0;\frac{1}{2} ight).

  • Câu 14: Vận dụng cao

    Với mọi góc \alpha, giá trị của biểu thức

    \cos\alpha + \cos\left( \alpha + \frac{\pi}{5} ight) + \cos\left( \alpha + \frac{2\pi}{5} ight) + ... + \cos\left( \alpha + \frac{9\pi}{5} ight)

    Ta có:

    \cos\alpha = - \cos\left( \alpha + \frac{5\pi}{5} ight)

    \cos\left( \alpha + \frac{\pi}{5} ight) = - \cos\left( \alpha + \frac{6\pi}{5} ight)

    \cos\left( \alpha + \frac{2\pi}{5} ight) = - \cos\left( \alpha + \frac{7\pi}{5} ight)

    \cos\left( \alpha + \frac{3\pi}{5} ight) = - \cos\left( \alpha + \frac{8\pi}{5} ight)

    \cos\left( \alpha + \frac{4\pi}{5} ight) = - \cos\left( \alpha + \frac{9\pi}{5} ight)

    Do đó:

    \cos\alpha + \cos\left( \alpha + \frac{\pi}{5} ight) + \cos\left( \alpha + \frac{2\pi}{5} ight) + ... + \cos\left( \alpha + \frac{9\pi}{5} ight) = 0

  • Câu 15: Nhận biết

    Vectơ có điểm đầu là D, điểm cuối là E được kí hiệu là

    Vectơ có điểm đầu là D, điểm cuối là E được kí hiệu là \overrightarrow{DE}.

  • Câu 16: Vận dụng

    Cho K(1; - 3). Điểm A \in Ox,B \in Oy sao cho A là trung điểm KB. Tìm tọa độ của điểm B.

    Ta có: A \in Ox,B \in Oy nên A(x;0),B(0;y).

    A là trung điểm KB nên \left\{ \begin{matrix} x = \frac{1 + 0}{2} \\ 0 = \frac{- 3 + y}{2} \\ \end{matrix} \Leftrightarrow ight.\ \left\{ \begin{matrix} x = \frac{1}{2} \\ y = 3 \\ \end{matrix} ight.

    Vậy B(0;3).

  • Câu 17: Vận dụng cao

    Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x4 − 4x3 − x2 + 10x − 3 trên đoạn [−1; 4] là

    Ta có y = x4 − 4x3 − x2 + 10x − 3 = x4 − 4x3 + 4x2 − 5x2 + 10x − 5 + 2

     = (x2−2x)2 − 5(x−1)2 + 2 = [(x−1)2−1]2 − 5(x−1)2 + 2.

    Đặt t = (x−1)2, x ∈ [−1; 4] ⇒ t ∈ [0; 9].

    y = (t - 1)^{2} - 5t + 2 = t^{2} - 7t + 3= \left( t - \frac{7}{2} ight)^{2} - \frac{37}{4}.

    Cách 1: Ta có 0 \leq \left( t -\frac{7}{2} ight)^{2} \leq \frac{121}{4} \Leftrightarrow -\frac{37}{4} \leq y \leq 21.

    Cách 2: Vẽ BBT

    Description: Capture

    Vậy y_{\min} = - \frac{37}{4}, ymax = 21.

  • Câu 18: Nhận biết

    Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2.

    Vì (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên điểm A(2;0) thuộc (P). Thay \left\{ \begin{matrix} x = 2 \\ y = 0 \\ \end{matrix} ight. vào (P), ta được 0 = 4a + 6 − 2 ⇔ a =  − 1.

    Vậy (P) : y =  − x2 + 3x − 2.

  • Câu 19: Vận dụng

    Cho ba mệnh đề: P: “số 20chia hết cho 5 và chia hết cho 2 ”

    Q: “ Số 35 chia hết cho 9”

    R: “ Số 17 là số nguyên tố ”

    Hãy tìm mệnh đề sai trong các mệnh đề dưới đây:

    P đúng, Q sai, R đúng.

    \overline{Q} đúng, R đúng nên \overline{Q} \Rightarrow Rđúng,

    P đúng, \overline{Q} \Rightarrow Rđúng nên P \Leftrightarrow \left( \overline{Q} \Rightarrow R ight)đúng, \left( \overline{Q} \Rightarrow R ight) \Rightarrow P đúng.

    R đúng, \overline{Q} đúng nên R \Leftrightarrow \overline{Q}đúng.

    R đúng, P đúng nên R \Rightarrow P đúng,

    R \Rightarrow P đúng, Q sai nên (R \Rightarrow P) \Rightarrow Q sai.

    Chọn đáp án (R \Rightarrow P) \Rightarrow Q.

  • Câu 20: Vận dụng

    Nghiệm của bất phương trình x - \frac{x^{2} - x + 6}{- x^{2} + 3x + 4} > 0 có

    x - \frac{x^{2} - x + 6}{- x^{2} + 3x + 4} = \frac{- x^{3} + 2x^{2} + 5x - 6}{- x^{2} + 3x + 4}

    = \frac{(x - 1)\left( - x^{2} + x + 6 ight)}{- x^{2} + 3x + 4}

    - x^{2} + x + 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 \\ x = 3 \\ \end{matrix} ight.\ ,\

    - x^{2} + 3x + 4 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 4 \\ \end{matrix} ight.

    Bảng xét dấu

    Suy ra

    x - \frac{x^{2} - x + 6}{- x^{2} + 3x + 4} > 0 \Leftrightarrow x \in ( - 2; - 1) \cup (1;3) \cup (4; + \infty).

    Vậy nghiệm của bất phương trình có 3 khoảng.

  • Câu 21: Thông hiểu

    Cho hai tập hợp A = ( - 3;5brack,B = \lbrack a; + \infty). Tìm a để A \cap B có đúng một phần tử.

    Để A \cap B có đúng một phần tử khi và chỉ khi a = 5. Khi đó A \cap B = \{ 5\}.

    Vậy a = 5 là giá trị cần tìm.

  • Câu 22: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 23: Nhận biết

    Trong mặt phẳng tọa độ Oxy cho 2 điểm M(2; 1) và N(1; 2). Tọa độ vectơ \overrightarrow{MN} là

    Ta có: 

    \overrightarrow {MN} = \left( {{x_N} - {x_M};{y_M} - {y_N}} ight) = \left( { - 1;1} ight)

  • Câu 24: Nhận biết

    Biết \overrightarrow{a},\overrightarrow{b}eq \overrightarrow{0} và \overrightarrow{a}\times \overrightarrow{b}=-|\overrightarrow{a}|\times |\overrightarrow{b}|. Câu nào sau đây đúng?

     Ta có:

    \begin{matrix} \vec a.\vec b = - |\vec a|.|\vec b| = |\vec a|.|\vec b|.\cos {180^0} \hfill \\ \Rightarrow \left( {\vec a,\vec b} ight) = {180^0} \hfill \\ \end{matrix}

    => \overrightarrow{a} và \overrightarrow{b} ngược hướng.

  • Câu 25: Thông hiểu

    Cho tam giác ABC và điểm M thỏa mãn \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0} Xác định vị trí điểm M.

    Giả sử G là trọng tâm tam giác ABC, khi đó ta có:

    \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0

    \Rightarrow M \equiv G

    => M là trọng tâm của tam giác ABC.

  • Câu 26: Thông hiểu

    Với giá trị nào của x thì mệnh đề chứa biến "\sqrt{x^{2}-3x+5}>2x+3" là đúng?

     Thay x=-1 vào 2 vế, ta được: 3>1 (đúng).

  • Câu 27: Vận dụng

    Tam giác ABC vuông tại A, có AB = c,\ \ AC = b. Gọi \mathcal{l}_{a} là độ dài đoạn phân giác trong góc \widehat{BAC}. Tính \mathcal{l}_{a} theo b và c.

    Ta có BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{b^{2} + c^{2}}

    Do AD là phân giác trong của \widehat{BAC}

    \Rightarrow BD = \frac{AB}{AC}.DC = \frac{c}{b}.DC = \frac{c}{b + c}.BC = \frac{c\sqrt{b^{2} + c^{2}}}{b + c}.

    Theo định lí hàm cosin, ta có

    BD^{2} = AB^{2} + AD^{2} - 2.AB.AD.cos\widehat{ABD} \Leftrightarrow \frac{c^{2}\left( b^{2} + c^{2} ight)}{(b + c)^{2}} = c^{2} + AD^{2} - 2c.AD.cos45{^\circ}

    \Rightarrow AD^{2} - c\sqrt{2}.AD + \left( c^{2} - \frac{c^{2}\left( b^{2} + c^{2} ight)}{(b + c)^{2}} ight) = 0 \Leftrightarrow AD^{2} - c\sqrt{2}.AD + \frac{2bc^{3}}{(b + c)^{2}} = 0.

    \Rightarrow AD = \frac{\sqrt{2}bc}{b + c} hay \mathcal{l}_{a} = \frac{\sqrt{2}bc}{b + c}.

  • Câu 28: Nhận biết

    Cách viết tập hợp nào đúng trong các cách viết sau để xác định tập hợp A các ước dương của 12:

    Các ước dương của 12 là: 1; 2; 3; 4; 6; 12

    => Cách viết tập hợp đúng là: A = \left \{ 1; 2; 3; 4; 6; 12ight \}

  • Câu 29: Thông hiểu

    Cho tam giác ABC, gọi M là trung điểm của BC và G là trọng tâm của tam giác ABC. Câu nào sau đây đúng?

    Do M là trung điểm của BC nên ta có: \overrightarrow{GB} + \overrightarrow{GC} = 2\overrightarrow{GM}.

  • Câu 30: Thông hiểu

    Tập xác định của hàm số f(x) = \sqrt{3 - x} + \frac{1}{\sqrt{x - 1}} là

    Hàm số xác định khi \left\{ \begin{matrix} 3 - x \geq 0 \\ x - 1 > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \leq 3 \\ x > 1 \\ \end{matrix} ight.\ \Leftrightarrow 1 < x \leq 3.

    Vậy tập xác định của hàm số là D = (1; 3].

  • Câu 31: Vận dụng

    Cho tam giác ABC với trực tâm H. D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng?

    Ta có BD là đường kính\Rightarrow \overrightarrow{OB} = \overrightarrow{DO}.

    Ta có AH\bot BC,DC\bot BC \Rightarrow AH//DC(1)

    Ta lại cóCH\bot AB,DA\bot AB \Rightarrow CH//DA(2)

    Từ (1)(2) \Rightarrowtứ giác HADC là hình bình hành\Rightarrow \overrightarrow{HA} = \overrightarrow{CD};\overrightarrow{AD} = \overrightarrow{HC}.

  • Câu 32: Thông hiểu

    Miền nghiệm của bất phương trình - 3x - 5y > 11 không chứa điểm nào sau đây?

    Xét điểm (1; - 3). Ta có: - 3.1 - 5.3 = - 18 > 11 không thỏa mãn. Do đó (1;3) không thuộc miền nghiệm của bất phương trình - 3x - 5y > 11.

  • Câu 33: Thông hiểu

    Tam giác ABC vuông ở A và có góc \widehat{B} = 50^{o}. Hệ thức nào sau đây là sai?

    Vì \left( \overrightarrow{AB},\ \overrightarrow{BC} ight) = 180^{0} - \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = 130^{o} nên loại \left( \overrightarrow{AB},\ \overrightarrow{BC} ight) = 130^{o}.

    Vì \left( \overrightarrow{BC},\ \overrightarrow{AC} ight) = \left( \overrightarrow{CB},\ \overrightarrow{CA} ight) = 40^{o} nên loại \left( \overrightarrow{BC},\ \overrightarrow{AC} ight) = 40^{o}.

    Vì \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = \left( \overrightarrow{BA},\ \overrightarrow{BC} ight) = 50^{o} nên loại \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = 50^{o}.

    Vì \left( \overrightarrow{AC},\ \overrightarrow{CB} ight) = 180^{0} - \left( \overrightarrow{CA},\ \overrightarrow{CB} ight) = 140^{o}nên chọn \left( \overrightarrow{AC},\ \overrightarrow{CB} ight) = 120^{o}.

  • Câu 34: Thông hiểu

    Cho hệ bất phương trình \left\{ \begin{matrix} 5x - 2y - 1 > 0 \\ 2x + 2y + 5 > 0 \\ x + y + 1 < 0 \\ \end{matrix} ight.. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

    Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

    Với O(0;0) \Rightarrow \left\{ \begin{matrix} 5.0 - 2.0 - 1 > 0 \\ 2.0 + 2.0 + 5 > 0 \\ 0 + 0 + 1 < 0 \\ \end{matrix} ight.. Bất phương trình thứ nhất sai nên không thỏa mãn.

    Với M(1;0) \Rightarrow \left\{ \begin{matrix} 5.1 - 2.0 - 1 > 0 \\ 2.1 + 2.0 + 5 > 0 \\ 1 + 0 + 1 < 0 \\ \end{matrix} ight.. Bất phương trình thứ ba sai nên không thỏa mãn.

    Với N(0; - 2) \Rightarrow \left\{ \begin{matrix} 5.0 - 2. - 2 - 1 > 0 \\ 2.0 + 2. - 2 + 5 > 0 \\ 0 - 2 + 1 < 0 \\ \end{matrix} ight.. Đúng. Chọn đáp án này.

  • Câu 35: Thông hiểu

    Trong mặt phẳng tọa độ Oxy, cho hai vectơ \overrightarrow{u} = (3;4) và \overrightarrow{v} = ( - \ 8;6). Khẳng định nào sau đây đúng?

    Vì \overrightarrow{u} = (3;4) \Rightarrow \left| \overrightarrow{u} ight| = \sqrt{3^{2} + 4^{2}} = 5 và \overrightarrow{v} = ( - \ 8;6) \Rightarrow \left| \overrightarrow{v} ight| = \sqrt{( - 8)^{2} + 6^{2}} = 10 nên đáp án \left| \overrightarrow{u} ight| = \left| \overrightarrow{v} ight| sai.

    Vì \frac{3}{- 8} eq \frac{4}{6} nên đáp án M\left( 0; - \frac{1}{2} ight). và \overrightarrow{v} cùng phương sai.

    Vì \overrightarrow{u}.\overrightarrow{v} = 3.( - 8) + 4.6 = 0 \Rightarrow \overrightarrow{u}\bot\overrightarrow{v} nên đáp án \overrightarrow{u} vuông góc với \overrightarrow{v} đúng.

  • Câu 36: Thông hiểu

    Diện tích tam giác có ba cạnh lần lượt là \sqrt{3},\sqrt{2} và 1 là:

    Nửa chu vi của tam giác là: p = \frac{{a + b + c}}{2} = \frac{{\sqrt 3 + \sqrt 2 + 1}}{2}

    Áp dụng công thức Herong ta có:

    \begin{matrix} S = \sqrt {p\left( {p - a} ight)\left( {p - b} ight)\left( {p - a} ight)} \hfill \\ S = \sqrt {p\left( {p - \sqrt 3 } ight)\left( {p - \sqrt 2 } ight)\left( {p - 1} ight)} \hfill \\ S = \dfrac{{\sqrt 2 }}{2} \hfill \\ \end{matrix}

  • Câu 37: Nhận biết

    Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

    Ta có: 3x - 7y > 19 là bất phương trình bậc nhất hai ẩn.

  • Câu 38: Thông hiểu

    Tam giác ABC có AB=\sqrt{2},AC=\sqrt{3} và \widehat{C}=45°. Tính độ dài cạnh BC.

     Áp dụng định lý côsin: A{B^2} = C{A^2} + C{B^2} - 2CA.CB.\cos 45^\circ\Leftrightarrow 2 = 3 + C{B^2} - 2\sqrt 3 .CB.\frac{{\sqrt 2 }}{2}\Leftrightarrow C{B^2} - \sqrt 6 CB + 1 = 0\Rightarrow BC=\frac{{\sqrt 6 + \sqrt 2 }}{2}.

     

  • Câu 39: Thông hiểu

    Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, AC, AB. Xác định các vectơ 

     \overrightarrow {PB} + \overrightarrow {MC} + \overrightarrow {NA}

    Ta có:

    \begin{matrix} \overrightarrow {PB} + \overrightarrow {MC} + \overrightarrow {NA} \hfill \\ = \overrightarrow {AP} + \overrightarrow {PN} + \overrightarrow {NA} \hfill \\ = \overrightarrow {AP} + \overrightarrow {PA} = \overrightarrow 0 \hfill \\ \end{matrix}

  • Câu 40: Nhận biết

    Tìm mệnh đề chứa biến.

    “x + 2 = 11.” là mệnh đề chứa biến.

  • Câu 41: Thông hiểu

    Cho \overrightarrow{a} = ( - 5;0),\ \overrightarrow{b} = (4;x). Tìm x để hai vectơ \overrightarrow{a},\ \overrightarrow{b} cùng phương.

    Hai vectơ \overrightarrow{a},\ \overrightarrow{b} cùng phương \Leftrightarrow - 5.x = 0.4\overset{}{ightarrow}x = 0.

  • Câu 42: Thông hiểu

    Cho bất phương trình m{x^2} - (2m - 1)x + m + 1 < 0 (1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.

    Để m{x^2} - (2m - 1)x + m + 1 < 0 thì m{x^2} - (2m - 1)x + m + 1 \geqslant 0 nghiệm đúng với \forall x \in \mathbb{R}.

    Nghĩa là:\left\{ {\begin{array}{*{20}{c}} {a > 0} \\ {\Delta \leqslant 0} \end{array}} ight.

    \begin{matrix} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {{{\left( {2m - 1} ight)}^2} - 4m\left( {m + 1} ight) \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {4{m^2} - 4m + 1 - 4{m^2} - 4m \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ { - 8m + 1 \leqslant 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m \geqslant \dfrac{1}{8}} \end{array}} ight. \Leftrightarrow m \geqslant \frac{1}{8} \hfill \\ \end{matrix}

  • Câu 43: Nhận biết

    Cho tam giác ABC có AB = 12,AC = 13,BC = 5. Diện tích S của tam giác ABC là:

    Ta có: BA^{2} + BC^{2} = AC^{2} nên tam giác ABC vuông tại B.

    Diện tích tam giác là: S = \frac{1}{2}BA \cdot BC = 30.

  • Câu 44: Vận dụng cao

    Tìm tất cả các giá trị thực âm của tham số m để hai khoảng ( - \infty;2m) và \left( \frac{2}{m}; + \infty ight) có khoảng giao khác rỗng.

    Với m < 0 thì \frac{2}{m} luôn có nghĩa. 

    Giao của hai tập đã cho khác rỗng khi hai tập hợp này có phần tử chung 

    \Leftrightarrow 2m > \frac{2}{m} \Leftrightarrow 2m^{2} < 2 (vì m < 0) \Leftrightarrow 2(m - 1)(m + 1) < 0

    Vì m < 0 nên ta xét các trường hợp sau

    Nếu m < - 1 thì m + 1 < 0,m - 1 < 0 = > 2(m - 1)(m + 1) > 0

    Vậy m < - 1 không thỏa yêu cầu bài toán.

    Nếu −1 < m < 0 thì m + 1 > 0,m - 1 < 0 \Rightarrow 2(m - 1)(m + 1) < 0

    Vậy giá trị cần tìm của m là - 1 < m < 0.

  • Câu 45: Thông hiểu

    Xác định parabol (P):y=ax^{2}+bx+2 biết rằng Parabol đi qua hai điểm M(1;5) và N(2;-2)

     Thay tọa độ M(1;5) và N(2;-2) vào hàm số, ta được:

    \left\{ {\begin{array}{*{20}{c}}{5 = a + b + 2}\\{ - 2 = 4a + 2b + 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 5}\\{b = 8}\end{array}} ight.} ight..

    Vậy đó là hàm số y=-5x^{2}+8x+2.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 48 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập