Cho biểu thức B xác định, rút gọn biểu thức
![]() với
với ![]() ?
?
Ta có:
Do đó:
Vì nên
Cho biểu thức B xác định, rút gọn biểu thức
![]() với
với ![]() ?
?
Ta có:
Do đó:
Vì nên
Cho ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Ta có:
và
.
Hai mệnh đề sau là mệnh đề gì: “x chia hết cho 9” và “x chia hết cho 3”.
Nếu x chia hết cho 9 thì x chia hết cho 3.
Nếu x chia hết cho 3 thì x có thể không chia hết cho 9.
=> Hai mệnh đề “x chia hết cho 9” và “x chia hết cho 3” là mệnh đề kéo theo.
Cho ![]() Tìm
Tìm ![]()
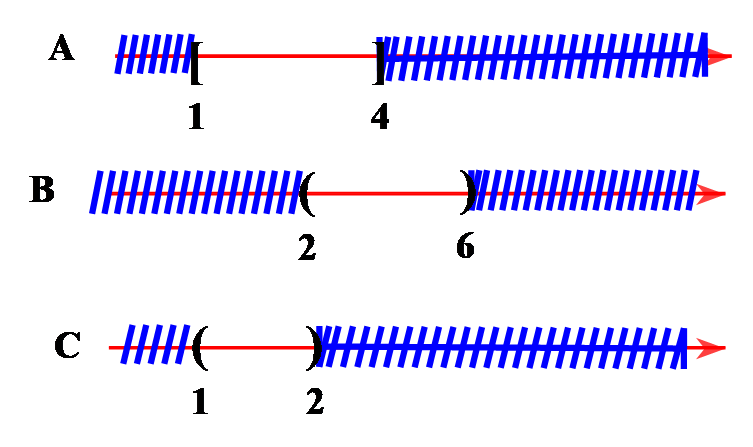
Vậy .
Cho ![]() và
và ![]() là hai vectơ cùng hướng và đều khác vectơ
là hai vectơ cùng hướng và đều khác vectơ ![]() .Trong các kết quả sau đây,hãy chọn kết quả đúng.
.Trong các kết quả sau đây,hãy chọn kết quả đúng.
Ta thấy vế trái của 4 phương án giống nhau.
Bài toán cho và
là hai vectơ cùng hướng và đều khác vectơ
suy ra
Do đó nên
Điểm kiểm tra môn Lịch Sử của một học sinh qua 8 lần thi được ghi lại như sau:
![]()
Biết số trung vị của mẫu số liệu trên bằng ![]() . Kết quả nào dưới đây đúng?
. Kết quả nào dưới đây đúng?
Vì là số chẵn nên trung vị của mẫu số liệu là trung bình cộng của số liện ở vị trí thứ 4 và thứ 5.
Suy ra
Vậy .
Cho bất phương trình ![]() (1). Chọn khẳng định đúng trong các khẳng định sau:
(1). Chọn khẳng định đúng trong các khẳng định sau:
Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Cho tứ giác ![]() . Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác?
. Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác?
Xét các vectơ có điểm là điểm đầu thì có các vectơ thỏa mãn bài toán là
có 3 vectơ.
Tương tự cho các điểm còn lại
Vậy chọn đáp án 12.
Tìm phát biểu không phải mệnh đề.
“Buồn ngủ quá!” là mệnh đề.
Người ta thường kí hiệu tập hợp số như thế nào?
Người ta thường kí hiệu các tập hợp số như sau:
Số quy tròn của số gần đúng ![]() với
với ![]() là:
là:
Quy tròn đến hàng trăm nên số quy tròn của số gần đúng
là:
.
Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() của tứ giác
của tứ giác ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Do M là trung điểm các cạnh AB nên .
Do N lần lượt là trung điểm các cạnh DC nên .
Ta có
Mặt khác
Do đó .
Tìm mốt của mẫu số liệu: 1 3 4 2 0 0 5 6.
Giá trị 0 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 0.
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm ![]() và
và ![]() . Mỗi sản phẩm
. Mỗi sản phẩm ![]() bán lãi
bán lãi ![]() nghìn đồng, mỗi sản phẩm
nghìn đồng, mỗi sản phẩm ![]() bán lãi
bán lãi ![]() nghìn đồng. Để sản xuất được một sản phẩm
nghìn đồng. Để sản xuất được một sản phẩm ![]() thì Chiến phải làm việc trong
thì Chiến phải làm việc trong ![]() giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong ![]() giờ. Để sản xuất được một sản phẩm
giờ. Để sản xuất được một sản phẩm ![]() thì Chiến phải làm việc trong
thì Chiến phải làm việc trong ![]() giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong ![]() giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá
giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá ![]() giờ và Bình không thể làm việc quá
giờ và Bình không thể làm việc quá ![]() giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.
giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.
Gọi ,
lần lượt là số sản phẩm loại
và loại
được sản xuất ra. Điều kiện
,
nguyên dương.
Ta có hệ bất phương trình sau:
Miền nghiệm của hệ trên là
Tiền lãi trong một tháng của xưởng là .
Ta thấy đạt giá trị lớn nhất chỉ có thể tại các điểm
,
,
. Vì
có tọa độ không nguyên nên loại.
Tại thì
triệu đồng.
Tại thì
triệu đồng.
Vậy tiền lãi lớn nhất trong một tháng của xưởng là triệu đồng.
Cho giá trị gần đúng của ![]() là 0,429. Sai số tuyệt đối của số 0,429 là:
là 0,429. Sai số tuyệt đối của số 0,429 là:
Ta có: nên sai số tuyệt đối của 0,429 là
Cho ![]() có
có ![]() Diện tích của tam giác là:
Diện tích của tam giác là:
Ta có:
Cho ba điểm ![]() phân biệt. Tập hợp những điểm
phân biệt. Tập hợp những điểm ![]() mà
mà ![]() là :
là :
Ta có:
.
Tập hợp điểm là đường thẳng đi qua
và vuông góc với
.
Trong mặt phẳng ![]() , cho
, cho ![]() và
và ![]() . Khẳng định nào sau đây là sai?
. Khẳng định nào sau đây là sai?
Ta có: nên đáp án Tích vô hướng của hai vectơ đã cho là
đúng.
Ta có: nên đáp án Độ lớn của vectơ
là
đúng.
Ta có: nên đáp án Độ lớn của vectơ
là
đúng.
Đáp án sai là Góc giữa hai vectơ là .
Trong hệ tọa độ ![]() cho ba điểm
cho ba điểm ![]() Tìm tọa độ của vectơ
Tìm tọa độ của vectơ ![]()
Ta có
Cách khác:
Cho hệ bất phương trình ![]() . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
Với . Ta có:
. Cả hai bất phương trình đều thỏa mãn. Chọn đáp án này.
Với ![]() (khác vectơ - không) thì độ dài đoạn
(khác vectơ - không) thì độ dài đoạn ![]() được gọi là
được gọi là
Với (khác vectơ - không) thì độ dài đoạn
được gọi là: Độ dài của
Cho tam giác ![]() có
có ![]() , độ dài các cạnh tam giác thỏa mãn biểu thức
, độ dài các cạnh tam giác thỏa mãn biểu thức ![]() . Tính độ lớn góc
. Tính độ lớn góc ![]() ?
?
Ta có:
Miền nghiệm của bất phương trình ![]() chứa điểm nào sau đây?
chứa điểm nào sau đây?
Xét điểm . Vì
nên miền nghiệm của bất phương trình chứa điểm
.
Cho hình bình hành ABCD tâm O. Khi đó ![]() bằng:
bằng:
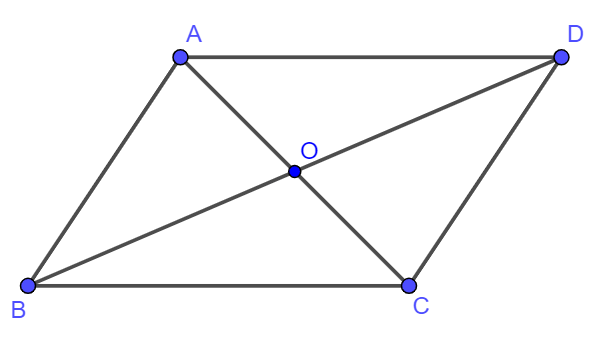
Ta có:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, AC, AB. Xác định các vectơ
![]()
Ta có:
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo ĐÚNG?
Nếu a chia hết cho 3 thì a chia hết cho 9 có mệnh đề đảo là Nếu a chia hết cho 9 thì a chia hết cho 3. Đây là mệnh đề đảo đúng.
Cho hai lực ![]() và
và ![]() có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực
có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực ![]() và
và ![]() lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là:
lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là:
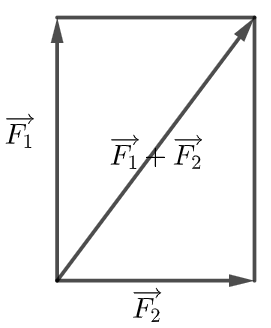
Ta có: .
Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?

Ta có: (Sai).
Bảng dưới đây thể hiện sản lượng lúa (đơn vị: tạ) của một số thửa ruộng:

Tính phương sai của mẫu số liệu.
Số trung bình của mẫu là:
.
Phương sai:
.
Cho tam giác ![]() , biết
, biết ![]() . Số đo góc
. Số đo góc ![]() là:
là:
Áp dụng hệ quả định lí cosin cho tam giác ABC ta có:
Trong mặt phẳng Oxy, cho ![]() và
và ![]() . Kết luận nào sau đây sai?
. Kết luận nào sau đây sai?
Ta có:
Vậy kết luận sai là:
Một công ty nhỏ gồm 1 giám đốc và 4 nhân viên. Thu nhập của giám đốc là 15 triệu đồng, thu nhập của nhân viên là 5 triệu đồng. Tìm trung vị cho mẫu số liệu về lương của các thành viên trong công ty.
Sắp xếp mẫu số liệu theo thứ tự không giảm: 5 5 5 5 15.
Dãy trên có giá trị chính giữa bằng 5.
Vậy trung vị của mẫu số liệu trên bằng 5.
Trong hệ tọa độ ![]() cho bốn điểm
cho bốn điểm ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Ta có ngược hướng.
Cho biết ![]() . Tính
. Tính ![]() .
.
Ta có:
.
Cho hai tập hợp ![]() ,
, ![]() . Tìm tất cả các giá trị của tham số
. Tìm tất cả các giá trị của tham số ![]() để
để ![]() .
.
Ta có:
Do đó để
Cho một mẫu dữ liệu đã được sắp xếp theo thứ tự không giảm ![]() . Khi đó khoảng biến thiên
. Khi đó khoảng biến thiên ![]() của mẫu số liệu bằng:
của mẫu số liệu bằng:
Khoảng biến thiên của mẫu số liệu bằng:
Gọi ![]() là trọng tâm tam giác vuông
là trọng tâm tam giác vuông ![]() với cạnh huyền
với cạnh huyền ![]() Tính độ dài của vectơ
Tính độ dài của vectơ ![]() .
.
Gọi là trung điểm của
Ta có
Xác định tập hợp ![]() bằng cách liệt kê các phần tử.
bằng cách liệt kê các phần tử.
Ta có: .
Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào ![]() là
là ![]() , chiều dài của hàng rào
, chiều dài của hàng rào ![]() là
là ![]() . Góc giữa hai hàng rào
. Góc giữa hai hàng rào ![]() và
và ![]() là
là ![]() (như hình vẽ)
(như hình vẽ)

Diện tích mảnh đất mà gia đình bà Sáu sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Diện tích mảnh đất của gia đình bà Sáu (tam giác ) là:
.
Điểm kiểm tra môn Văn của 2 tổ học sinh được thống kê:

Dựa vào khoảng biến thiên thì tổ nào học đều hơn?
Khoảng biến thiên điểm của tổ 1 là .
Khoảng biến thiên điểm của bạn Bình là .
Vì nên tổ 1 học đều hơn.
Trong mặt phẳng tọa độ Oxy, cho ![]() . Đâu là tọa độ của điểm A?
. Đâu là tọa độ của điểm A?
Ta có: O(0; 0)
Tam giác ![]() có
có ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Áp dụng định lí sin:
.
Cho bảng tần số như sau:
Giá trị | x1 | x2 | x3 | x4 | x5 | x6 |
Tần số | 15 | 9n - 1 | 12 |
| 10 | 17 |
Tìm n để ![]() là hai mốt của bảng tần số trên.
là hai mốt của bảng tần số trên.
Ta có:
Vậy n = 8.
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Ta có:
Diện tích ban đầu của tam giác là:
Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác là:
Một cửa hàng bán hai loại mặt hàng ![]() và
và ![]() . Biết rằng cứ bán một mặt hàng loại
. Biết rằng cứ bán một mặt hàng loại ![]() cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại
cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại ![]() cửa hàng lãi 7 nghìn đồng. Gọi
cửa hàng lãi 7 nghìn đồng. Gọi ![]() lần lượt là số mặt hàng loại
lần lượt là số mặt hàng loại ![]() và mặt hàng loại
và mặt hàng loại ![]() mà cửa hàng đó bán ra trong một tháng. Cặp số
mà cửa hàng đó bán ra trong một tháng. Cặp số ![]() nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
Đặt x là số tiền lãi của mặt hàng A
y là số tiền lãi của mặt hàng B
Đổi 30 triệu = 30 000 nghìn đồng
Theo đề bài ta có:
TH1: Thay A (1000; 2000) vào phương trình
. Thay B(3000; 1000
vào phương trình
: Thay C
vào phương trình
TH4: Thay vào phương trình
Vậy đáp án là: C
