Lớp 10 Toán 10 - Kết nối tri thức

Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2

Mô tả thêm: Đề thi học kì 1 Toán 10 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức Toán 10 Kết nối tri thức.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Cho tam giác đều ABC có đường cao AH. Tính (\overrightarrow{AH},\overrightarrow{BA}).

     Lấy D sao cho \overrightarrow {BD}=\overrightarrow {AH}.

    Ta có: (\overrightarrow{AH},\overrightarrow{BA}) =(\overrightarrow{BD},\overrightarrow{BA})=90^{\circ} +60^{\circ}= 150^{\circ}.

  • Câu 2: Thông hiểu

    Biết rằng hai vec tơ \overrightarrow{a} và \overrightarrow{b} không cùng phương nhưng hai vectơ 2\overrightarrow{a} - 3\overrightarrow{b} và \overrightarrow{a} + (x - 1)\overrightarrow{b} cùng phương. Khi đó giá trị của x là:

    Ta có: 2\overrightarrow{a} - 3\overrightarrow{b} và \overrightarrow{a} + (x - 1)\overrightarrow{b} cùng phương nên có tỉ lệ: \frac{1}{2} = \frac{x - 1}{- 3} \Rightarrow x = - \frac{1}{2}.

  • Câu 3: Thông hiểu

    Kết quả đo chiều dài của một cây cầu được ghi là 152m \pm 0,2m. Tìm sai số tương đối của phép đo chiều dài cây cầu.

    Phép đo cây cầu có sai số tương đối thỏa mãn \delta < \frac{0,2}{152} \approx 0,1316\%.

  • Câu 4: Vận dụng

    Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?

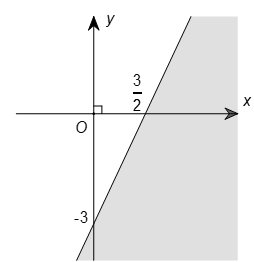
    Đường thẳng đi qua hai điểm A\left( \frac{3}{2};0 ight) và B(0; - 3) nên có phương trình 2x - y = 3.

    Mặt khác, cặp số (0;0) không thỏa mãn bất phương trình 2x - y > 3 nên phần tô đậm ở hình trên biểu diễn miền nghiệm của bất phương trình 2x - y > 3.

  • Câu 5: Thông hiểu

    Tìm m để hệ bất phương trình sau trở thành hệ bất phương trình bậc nhất hai ẩn: \left\{\begin{matrix}mx^{2}+2(m+1)x+y<1\\ my^{2}+3x-4y-1>0\end{matrix}ight..

    Để hệ bất phương trình \left\{\begin{matrix}mx^{2}+2(m+1)x+y<1\\ my^{2}+3x-4y-1>0\end{matrix}ight. trở thành hệ bất phương trình bậc nhất hai ẩn thì hệ số đứng trước x^2,y^2 phải bằng 0 nghĩa là:

    m=0

    Vậy với m=0 thì hệ bất phương trình đã cho trở thành hệ bất phương trình bậc nhất hai ẩn.

  • Câu 6: Thông hiểu

    Cho tam giác ABC có b = 7; c = 5, \cos A = \frac{3}{5}. Đường cao h_{a} của tam giác ABC là:

    Ta có: a^{2} = b^{2} + c^{2} - 2bc\cos A = 7^{2} + 5^{2} - 2.7.5.\frac{3}{5} = 32 \Rightarrow a = 4\sqrt{2}.

    Mặt khác: sin^{2}A + cos^{2}A = 1 \Rightarrow sin^{2}A = 1 - cos^{2}A = 1 - \frac{9}{25} = \frac{16}{25} \Rightarrow \sin A = \frac{4}{5} (Vì \sin A > 0).

    Mà: S_{\Delta ABC} = \frac{1}{2}b.c.sinA = \frac{1}{2}a.h_{a} \Rightarrow h_{a} = \frac{bc\sin A}{a} = \frac{7.5.\frac{4}{5}}{4\sqrt{2}} = \frac{7\sqrt{2}}{2}.

  • Câu 7: Nhận biết

    Cho \overrightarrow{a} = (3; - 4),\ \overrightarrow{b} = ( - 1;2). Tìm tọa độ của vectơ \overrightarrow{a} + \overrightarrow{b}.

    Ta có \overrightarrow{a} + \overrightarrow{b} = \left( 3 + ( - 1); - 4 + 2 ight) = (2; - 2).

  • Câu 8: Nhận biết

    Cho tam giác ABC. Gọi Mvà N lần lượt là trung điểm của AB và AC. Khẳng định nào sau đây sai?

    Vì M,\ \ N lần lượt là trung điểm của AB,\ \ AC. Suy ra MN là đường trung bình của tam giác

    ABC\overset{}{ightarrow}MN = \frac{1}{2}BC. Mà \overrightarrow{BC},\ \ \ \overrightarrow{MN} là hai vectơ cùng hướng nên \overrightarrow{BC} = 2\ \overrightarrow{MN}.

  • Câu 9: Vận dụng

    Cho A(1;2),\ B( - 2;6). Điểm M trên trục Oy sao cho ba điểm A,B,M thẳng hàng thì tọa độ điểm M là:

    Ta có: M trên trục Oy \Rightarrow M(0;y).

    Ba điểm A,B,M thẳng hàng khi \overrightarrow{AB} cùng phương với \overrightarrow{AM}.

    Ta có \overrightarrow{AB} = ( - 3;4),\ \ \overrightarrow{AM} = ( - 1;y - 2). Do đó, \overrightarrow{AB} cùng phương với \overrightarrow{AM} \Leftrightarrow \frac{- 1}{- 3} = \frac{y - 2}{4} \Rightarrow y = \frac{10}{3}. Vậy M\left( 0;\frac{10}{3} ight).Đáp án là M\left( 0;\frac{10}{3} ight)

  • Câu 10: Vận dụng

    Cho dữ liệu thống kê số vốn (đơn vị: triệu đồng) mua phân bón vụ mùa của 10 hộ nông dân ở thôn B như sau:

    2,9;\ 1,2;\ 1,1;\ 0,8;\ 3,5;\ 1,6;\ 1,8;\ 1,2;\ 1,3;\ 0,7

    Tìm các giá trị bất thường của mẫu số liệu đã cho?

    Sắp xếp dãy số liệu theo thứ tự không giảm ta được:

    \ 0,7;\ 0,8;1,1;\ 1,2;\ 1,2;\ 1,3;\ 1,6;\ 1,8;\ 2,9;\ 3,5

    Ta xác định được các tứ phân vị:\left\{ \begin{matrix} Q_{2} = 1,25 \\ Q_{1} = 1,1 \\ Q_{3} = 1,8 \\ \end{matrix} ight.

    \Rightarrow \Delta Q = Q_{3} - Q_{1} = 1,8 - 1,1 = 0,7

    \Rightarrow \left\{ \begin{matrix}Q_{1} - \dfrac{3}{2}\Delta Q = 0,05 \\Q_{3} + \dfrac{1}{2}\Delta Q = 2,85 \\\end{matrix} ight.

    Suy ra có hai giá trị bất thường là 2,9;\ 3,5.

  • Câu 11: Vận dụng cao

    Cho tam giác ABC có AB = c;BC = a;AC = b, độ dài các cạnh tam giác thỏa mãn biểu thức \frac{1}{a + b} + \frac{1}{b + c} = \frac{3}{a + b + c}. Tính độ lớn góc \widehat{B}?

    Ta có:

    \frac{1}{a + b} + \frac{1}{b + c} = \frac{3}{a + b + c}

    \Leftrightarrow \frac{a + b + c}{a + b} + \frac{a + b + c}{b + c} = 3

    \Leftrightarrow 1 + \frac{c}{a + b} + 1 + \frac{a}{b + c} = 3

    \Leftrightarrow \frac{c}{a + b} + \frac{a}{b + c} = 1

    \Leftrightarrow c(b + c) + a(a + b) = (b + c)(a + b)

    \Leftrightarrow c^{2} + cb + a^{2} + ab = ab + b^{2} + ac + bc

    \Leftrightarrow c^{2} + a^{2} - b^{2} = ac

    \Leftrightarrow \frac{c^{2} + a^{2} - b^{2}}{2ac} = \frac{1}{2}

    \Leftrightarrow \cos\widehat{B} = \frac{1}{2}

    \Leftrightarrow \widehat{B} = 60^{0}

  • Câu 12: Vận dụng

    Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang góc 30^{0}, phương nhìn BC tạo với phương nằm ngang góc 15^{0}30'. Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?

    Từ giả thiết, ta suy ra tam giác ABC có \widehat{CAB} = 60^{0},\ \ \widehat{ABC} = 105^{0}30' và c = 70. Khi đó \widehat{A} + \widehat{B} + \widehat{C} = 180^{0} \Leftrightarrow \widehat{C} = 180^{0} - \left( \widehat{A} + \widehat{B} ight) = 180^{0} - 165^{0}30' = 14^{0}30'.

    Theo định lí sin, ta có \frac{b}{\sin B} = \frac{c}{\sin C} hay \frac{b}{sin105^{0}30'} = \frac{70}{sin14^{0}30'}

    Do đó AC = b = \frac{70.sin105^{0}30'}{sin14^{0}30'} \approx 269,4m.

    Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 30^{0} nên

    CH = \frac{AC}{2} = \frac{269,4}{2} = 134,7\ m. Vậy ngọn núi cao khoảng 135m.

  • Câu 13: Thông hiểu

    Điểm nào sau đây thuộc miền nghiệm của bất phương trình 2x + y - 3 > 0?

    Xét điểm M\left( 1;\frac{3}{2}ight) . Ta có: 2.1 + \frac{3}{2}- 3 = \frac{1}{2} > 0 nên M\left( 1;\frac{3}{2} ight) thuộc miền nghiệm của bất phương trình đã cho.

  • Câu 14: Nhận biết

    Gọi M,\ \ N lần lượt là trung điểm của các cạnh AB,\ \ AC của tam giác đều ABC. Hỏi cặp vectơ nào sau đây cùng hướng?

    Cặp \overrightarrow{AB} và \overrightarrow{MB} là cặp vectơ cùng hướng.

  • Câu 15: Vận dụng cao

    Cho hai số thực x, y thoả mãn x \in \lbrack 1;2brack,y \in \lbrack 5;7brack. Hãy tìm giá trị nhỏ nhất m và lớn nhất M của biểu thức P = |2x - y|.

    Từ giả thiết suy ra 2x \in \lbrack 2;4brack và y \in \lbrack 5;7brack, P chính là khoảng cách giữa 2 số 2x và y trên trục số.

    P nhỏ nhất khi 2x = 4 và y = 5; P lớn nhất khi 2x = 2 và y = 7.

    Vậy m = 1,M = 5.

  • Câu 16: Thông hiểu

    Miền nghiệm của bất phương trình \left( 1 + \sqrt{3} ight)x - \left( 1 - \sqrt{3} ight)y \geq 2 chứa điểm nào sau đây?

    Xét điểm A(1\ \ ;\ \ - 1). Vì \left( 1 + \sqrt{3} ight).1 - \left( 1 - \sqrt{3} ight).( - 1) = 2 \geq 2 nên miền nghiệm của bất phương trình chứa điểm A(1\ \ ;\ \ - 1).

  • Câu 17: Thông hiểu

    Cho tam giác ABC có M thỏa mãn điều kiện \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = \overrightarrow{0}. Xác định vị trí điểm M.

    Gọi G là trọng tâm tam giác ABC.

    Ta có \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0} \Rightarrow M \equiv G.

  • Câu 18: Thông hiểu

    Tập hợp A = \left\{ 1,2,3,4,5,6 ight\} có bao nhiêu tập hợp con gồm 2 phần tử:

    Tập A gồm 6 phần tử.

    Mỗi phần tử ghép với 1 phần tử còn lại ta được 1 tập con của A có 2 phần tử.

    Số tập con của A có 2 phần tử bằng: \frac{6.5}{2} = 15.

  • Câu 19: Nhận biết

    Cho hình bình hành ABCD. Với mọi điểm M, ta có khẳng định nào sau đây:

     Ta có: \overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{MC}-\overrightarrow{MD} \Leftrightarrow \overrightarrow {AB}= \overrightarrow {DC} (Đúng).

  • Câu 20: Nhận biết

    Cho mẫu số liệu như sau:

    Khoảng biến thiên của mẫu số liệu trên là:

    Quan sát mẫu số liệu ta thấy:

    Giá trị lớn nhất là 29.

    Giá trị nhỏ nhất là 23

    Suy ra khoảng biến thiên của mẫu số liệu là: 29 – 23 = 6.

    Vậy đáp án là 6.

  • Câu 21: Vận dụng cao

    Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.

    Gọi x, y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x, y nguyên dương.

    Ta có hệ bất phương trình sau: \left\{ \begin{matrix} 3x + 2y \leq 180 \\ x + 6y \leq 220 \\ x > 0 \\ y > 0 \\ \end{matrix} ight.

    Miền nghiệm của hệ trên là

    Tiền lãi trong một tháng của xưởng là T = 0,5x + 0,4y .

    Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A, B, C. Vì C có tọa độ không nguyên nên loại.

    Tại A(60;\ 0) thì T = 30 triệu đồng.

    Tại B(40;\ 30) thì T = 32 triệu đồng.

    Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

  • Câu 22: Thông hiểu

    Một công ty nhỏ gồm 1 giám đốc và 4 nhân viên. Thu nhập của giám đốc là 15 triệu đồng, thu nhập của nhân viên là 5 triệu đồng. Tìm trung vị cho mẫu số liệu về lương của các thành viên trong công ty.

    Sắp xếp mẫu số liệu theo thứ tự không giảm: 5 5 5 5 15.

    Dãy trên có giá trị chính giữa bằng 5.

    Vậy trung vị của mẫu số liệu trên bằng 5.

  • Câu 23: Thông hiểu

    Cho mệnh đề A: “\forall x \in R,x^{2} - x + 7 < 0”. Mệnh đề phủ định của A là:

    Phủ định của \forall là \exists.

    Phủ định của < là \geq.

    Mệnh đề phủ định của A: \exists x \in R,x^{2} - \ x + 7 \geq 0.

  • Câu 24: Nhận biết

    Phát biểu lại mệnh đề "Nếu n = 2 thì 2n^{2}+1 là một hợp số".

     Phát biểu lại mệnh đề trên: "n = 2 là điều kiện đủ để 2n^{2}+1 là một hợp số".

  • Câu 25: Vận dụng

    Phần không tô đậm trong hình vẽ dưới đây, biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?

    Do miền nghiệm không chứa biên nên ta loại đáp án \left\{ \begin{matrix} x - 2y \leq 0 \\ x + 3y \geq - 2 \\ \end{matrix} ight. và \left\{ \begin{matrix} x - 2y \leq 0 \\ x + 3y \leq - 2 \\ \end{matrix} ight.. Chọn điểm M(0;1)thử vào các hệ bất phương trình.

    Xét đáp án \left\{ \begin{matrix} x - 2y > 0 \\ x + 3y < - 2 \\ \end{matrix} ight., ta có \left\{ \begin{matrix} 0 - 2.1 > 0 \\ 0 + 3.1 < - 2 \\ \end{matrix} ight.. Sai.

    Vậy chọn đáp án \left\{ \begin{matrix} x - 2y < 0 \\ x + 3y > - 2 \\ \end{matrix} ight..

  • Câu 26: Nhận biết

    Mệnh đề nào sau đây đúng?

    Vì vectơ - không cùng phương với mọi vectơ.

  • Câu 27: Nhận biết

    Một shop bán giày thống kê số lượng giày bán trong vài ngày trong bảng sau:

    Cỡ giày

    37

    38

    39

    40

    41

    42

    Số lượng

    35

    42

    50

    38

    32

    48

    Mốt của bảng số liệu trên là:

    Mốt là giá trị có tần số lớn nhất trong bảng số liệu

    Quan sát bảng số liệu đã cho suy ra mốt của bảng số liệu là 39.

  • Câu 28: Thông hiểu

    Hãy liệt kê các phần tử của tập hợp \mathbf{X =}\left\{ \mathbf{x}\mathbb{\in R}\mathbf{|}\mathbf{x}^{\mathbf{2}}\mathbf{+ x +}\mathbf{1}\mathbf{=}\mathbf{0} ight\}\mathbf{.}

    Ta có: x^{2} + x + 1 = 0 không có nghiệm thực.

  • Câu 29: Nhận biết

    Tập X = \left\{ x\mathbb{\in R}|2x^{2} - 5x + 3 = 0 ight\} bằng tập nào sau đây?

    Ta có: 2x^{2} - 5x + 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = \frac{3}{2} \\ \end{matrix} ight.\ \Rightarrow X = \left\{ 1;\frac{3}{2} ight\}.

  • Câu 30: Vận dụng

    Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = \lbrack - 4;4brack \cup \lbrack 7;9brack \cup \lbrack 1;7).

    Vậy A = \lbrack - 4;4brack \cup \lbrack 7;9brack \cup \lbrack 1;7) = \lbrack - 4;9brack.

  • Câu 31: Nhận biết

    Làm tròn số 1234,567 đến hàng đơn vị?

    Số 1234,567 làm tròn đến hàng đơn vị là 1235.

  • Câu 32: Thông hiểu

    Cho góc \alpha thỏa mãn \cos\alpha = - \frac{12}{13} và \frac{\pi}{2} < \alpha < \pi. Tính \tan\alpha.

    Ta có \left\{ \begin{matrix} \sin\alpha = \pm \sqrt{1 - cos^{2}\alpha} = \pm \frac{5}{13} \\ \frac{\pi}{2} < \alpha < \pi. \\ \end{matrix} ight. \overset{}{ightarrow}\sin\alpha = \frac{5}{13}\overset{}{ightarrow}\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = - \frac{5}{12}.

  • Câu 33: Nhận biết

    Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \left\{\begin{matrix}2x-5y-1>0\\ 2x+y+5>0 \\ x+y+1<0 \end{matrix}ight.

     Thay tọa độ (0;– 2) vào hệ ta được: \left\{\begin{matrix}2.0-5(-2)-1>0\\ 2.0-2+5>0 \\ 0-2+1<0 \end{matrix}ight. ta thấy cả 3 bất phương trình đều thỏa mãn. Do đó điểm này thuộc miền nghiệm của hệ.

  • Câu 34: Thông hiểu

    Cho tam giác ABC. Tập hợp các điểm M thỏa mãn \overrightarrow{MA}\times \overrightarrow{BC}=0 là:

    Ta có:

    \begin{matrix} \overrightarrow {MA} .\overrightarrow {BC} = 0 \Rightarrow \left| {\overrightarrow {MA} } ight|.\left| {\overrightarrow {BC} } ight|\cos \left( {\overrightarrow {MA} ,\overrightarrow {BC} } ight) = 0 \hfill \\ \Leftrightarrow \cos \left( {\overrightarrow {MA} ,\overrightarrow {BC} } ight) = 0 \hfill \\ \Leftrightarrow \left( {\overrightarrow {MA} ,\overrightarrow {BC} } ight) = {90^0} \hfill \\ \Leftrightarrow \overrightarrow {MA} \bot \overrightarrow {BC} \hfill \\ \Leftrightarrow MA \bot BC \hfill \\ \end{matrix}

    Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.

  • Câu 35: Thông hiểu

    Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \widehat{ACB} = 60{^\circ}. Tính độ dài cạnh cạnh BC.

    Gọi M,\ \ N lần lượt là trung điểm của AB,\ \ BC.

    \overset{}{ightarrow}MN là đường trung bình của \Delta ABC.

    \overset{}{ightarrow}MN = \frac{1}{2}AC. Mà MN = 3, suy ra AC = 6.

    Theo định lí hàm cosin, ta có:

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{ACB}

    \Leftrightarrow 9^{2} = 6^{2} + BC^{2} - 2.6.BC.cos60{^\circ}

    \Rightarrow BC = 3 + 3\sqrt{6}

  • Câu 36: Vận dụng

    Cho góc \alpha thỏa mãn 0 < \alpha < \frac{\pi}{4} và \sin\alpha + \cos\alpha = \frac{\sqrt{5}}{2}. Tính P = \sin\alpha - \cos\alpha.

    Ta có \left( \sin\alpha - \cos\alpha ight)^{2} + \left( \sin\alpha + \cos\alpha ight)^{2} = 2\left( sin^{2}\alpha + cos^{2}\alpha ight) = 2.

    Suy ra \left( \sin\alpha - \cos\alpha ight)^{2} = 2 - \left( \sin\alpha + \cos\alpha ight)^{2} = 2 - \frac{5}{4} = \frac{3}{4}.

    Do 0 < \alpha < \frac{\pi}{4} suy ra \sin\alpha < \cos\alpha nên \sin\alpha - \cos\alpha < 0. Vậy P = - \frac{\sqrt{3}}{2}.

  • Câu 37: Vận dụng

    Gọi AN,\ CM là các trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?

    Ta có \overrightarrow{AN} = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} ight) = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}

    \overrightarrow{CM} = \overrightarrow{CA} + \overrightarrow{AM} \Rightarrow \frac{1}{2}\overrightarrow{CM} = \frac{1}{2}\overrightarrow{CA} + \frac{1}{2}\overrightarrow{AM}

    Suy ra

    \overrightarrow{AN} +\frac{1}{2}\overrightarrow{CM} =\frac{1}{2}\overrightarrow{AB} +\frac{1}{2}\overrightarrow{AC} + \frac{1}{2}\overrightarrow{CA} +\frac{1}{2}\overrightarrow{AM}= \frac{1}{2}\overrightarrow{AB} +\frac{1}{2}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AC} +\frac{1}{2} \cdot \frac{1}{2}\overrightarrow{AB} =\frac{3}{4}\overrightarrow{AB}

    Do đó \overrightarrow{AB} = \frac{4}{3}\overrightarrow{AN} + \frac{2}{3}\overrightarrow{CM}.

  • Câu 38: Nhận biết

    Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y < 1?

     Thay (0; 1) vào bất phương trình, ta được: 1 < 1 (sai). Do đó cặp số này không là nghiệm của bất phương trình.

  • Câu 39: Nhận biết

    Tam giác ABC có \hat B = {60^0},\hat C = {45^0};AC = 5. Độ dài cạnh AB là:

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin B}} = \dfrac{{AB}}{{\sin C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin C}}{{\sin B}} = \dfrac{{5.\sin {{45}^0}}}{{\sin {{60}^0}}} = \dfrac{{5\sqrt 6 }}{3} \hfill \\ \end{matrix}

  • Câu 40: Nhận biết

    Tam giác ABC có AB=5,BC=7,CA=8. Số đo góc \hat A bằng:

     Áp dụng định lí côsin:

    \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}= \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.

    Suy ra \hat A = 60^{\circ}.

  • Câu 41: Vận dụng cao

    Cho tam giác ABC có M là trung điểm của BC. Điểm E xác định 2\overrightarrow{EA} + \overrightarrow{EC} = \overrightarrow{0}. Đường thẳng d đi qua E song song với AB cắt AM,BC lần lượt tại D;F. Điểm G nằm trên cạnh AB sao cho diện tích các tam giác BFG và ADE bằng nhau. Biết \overrightarrow{AG} = \alpha\overrightarrow{AB}. Tính giá trị của \alpha?

    Hình vẽ minh họa:

    Theo định lí Ta – lét ta có:

    \frac{FB}{FC} = \frac{EA}{EC} = \frac{1}{2} \Rightarrow FC = \frac{2}{3}BC

    \Rightarrow FM = \frac{2}{3}BC - MC = \frac{2}{3}BC - \frac{1}{2}BC = \frac{1}{6}BC

    \Rightarrow \overrightarrow{FM} = \frac{1}{4}\overrightarrow{FC}

    Mặt khác \overrightarrow{EC} = - 2\overrightarrow{EA};\overrightarrow{DA} = - \frac{DA}{DM}.\overrightarrow{DM} mà ba điểm D;E;F thẳng hàng nên theo định lí Menelaus ta được:

    \left( - \frac{DA}{DM} ight).\frac{1}{4}.( - 2) = 1

    \Rightarrow \frac{DA}{DM} = 2

    Ta có:

    \overrightarrow{AD} = \frac{2}{3}\overrightarrow{AM} = \frac{2}{3}.\frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} ight) = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}

    Chú ý rằng khoảng cách từ F đến AB bằng khoảng cách từ A đến DE nên hai tam giác ADE và BGF có cùng diện tích suy ra BG = DE do đó \overrightarrow{BG} = \overrightarrow{DE}

    Ta có:

    \overrightarrow{AE} = \overrightarrow{AD} + \overrightarrow{DE} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC} + \overrightarrow{BG}

    Mà \overrightarrow{AE} = \frac{1}{3}\overrightarrow{AC} \Rightarrow \overrightarrow{BG} = \frac{1}{3}\overrightarrow{BA}

    Hay \overrightarrow{AG} = \frac{2}{3}\overrightarrow{AB}

    Vậy \alpha = \frac{2}{3}

  • Câu 42: Vận dụng

    Cho đường tròn O và hai tiếp tuyến song song với nhau tiếp xúc với (O) tại hai điểm A và B. Mệnh đề nào sau đây đúng?

    Do hai tiếp tuyến song song và A,\ \ B là hai tiếp điểm nên AB là đường kính.

    Do đó O là trung điểm của AB.

    Suy ra \overrightarrow{OA} = - \overrightarrow{OB}.

  • Câu 43: Thông hiểu

    Cho mẫu số liệu: 0;5;5;5;6;6;6;7;8;10. Xác định khoảng tứ phân vị của mẫu số liệu?

    Ta có N = 10

    Suy ra Q_{2} = \frac{6 + 6}{2} = 6

    \Rightarrow \left\{ \begin{matrix} Q_{1} = 5 \\ Q_{3} = 7 \\ \end{matrix} ight.\ \Rightarrow \Delta Q = 7 - 5 = 2

    Vậy khoảng tứ phân vị bằng 2.

  • Câu 44: Thông hiểu

    Cho hai vectơ \overrightarrow{a} và \overrightarrow{b} khác \overrightarrow{0}. Xác định góc \alpha giữa hai vectơ \overrightarrow{a} và \overrightarrow{b} khi \overrightarrow{a}.\overrightarrow{b} = - \left| \overrightarrow{a} ight|.|\overrightarrow{b}|.

    Ta có \overrightarrow{a}.\overrightarrow{b} = \left|\overrightarrow{a} ight|.\left| \overrightarrow{b}ight|.\cos(\overrightarrow{a},\overrightarrow{b}).

    Mà theo giả thiết \overrightarrow{a}.\overrightarrow{b} = - \left|\overrightarrow{a} ight|.|\overrightarrow{b}|

    Suy ra \cos(\overrightarrow{a},\overrightarrow{b}) = - 1\longrightarrow (\overrightarrow{a},\overrightarrow{b}) =180^{\circ}

  • Câu 45: Thông hiểu

    Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng 5\sqrt{5} là:

    Ta có:

    \begin{matrix} \overrightarrow {AB} = \left( {x - 6;10} ight) \hfill \\ \Rightarrow \left| {\overrightarrow {AB} } ight| = \sqrt {{{\left( {x - 6} ight)}^2} + {{10}^2}} \hfill \\ \left| {\overrightarrow {AB} } ight| = 5\sqrt 5 \hfill \\ \Leftrightarrow \sqrt {{{\left( {x - 6} ight)}^2} + {{10}^2}} = 5\sqrt 5 \hfill \\ \Leftrightarrow {x^2} - 12x + 136 = 125 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 11} \\ {x = 1} \end{array}} ight. \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 16 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập