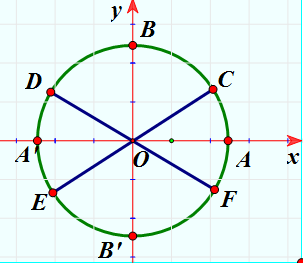
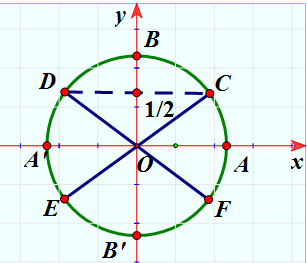
Cho hai đồ thị hàm số ![]() và
và ![]() , khi đó:
, khi đó:
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số:![]() Đúng||Sai
Đúng||Sai
b) Hoành độ giao điểm của hai đồ thị là ![]() Đúng||Sai
Đúng||Sai
c) Khi ![]() thì hai đồ thị hàm số cắt nhau tại ba điểm Sai||Đúng
thì hai đồ thị hàm số cắt nhau tại ba điểm Sai||Đúng
d) Khi ![]() thì toạ độ giao điểm của hai đồ thị hàm số là:
thì toạ độ giao điểm của hai đồ thị hàm số là: ![]() . Sai||Đúng
. Sai||Đúng
Cho hai đồ thị hàm số và
, khi đó:
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: Đúng||Sai
b) Hoành độ giao điểm của hai đồ thị là Đúng||Sai
c) Khi thì hai đồ thị hàm số cắt nhau tại ba điểm Sai||Đúng
d) Khi thì toạ độ giao điểm của hai đồ thị hàm số là:
. Sai||Đúng
Phương trình hoành độ giao điểm của hai đồ thị hàm số:
Vì .
Với với
.
Vậy toạ độ giao điểm của hai đồ thị hàm số là: .
Kết luận:
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |








 . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?