Lớp 11 Toán 11 - Cánh Diều

Đề thi học kì 1 Toán 11 Cánh Diều Đề 3

Mô tả thêm: Đề thi cuối kì 1 Toán 11 được biên soạn gồm các câu hỏi trắc nghiệm thuộc 4 chuyên đề trọng tâm Toán 11 sách Cánh Diều giúp bạn tổng hợp kiến thức và rèn luyện kĩ năng làm bài kiểm tra học kì sắp tới.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng

    Tổng các nghiệm của phương trình \cos\left( \sin x ight) = 1 trên đoạn (0;2\pibrack bằng:

    Phương trình tương đương với \sin x = k2\pi;k\mathbb{\in Z}

    Vì - 1 \leq \sin x \leq 1 nên k = 0

    Khi đó phương trình trở thành \sin x = 0 \Rightarrow x = l\pi;\left( l\mathbb{\in Z} ight)

    Vì x \in (0;2\pibrack nên x \in \left\{ 0;\pi ight\}

    => Tổng các nghiệm của phương trình là: 0 + \pi = \pi

  • Câu 2: Nhận biết

    Mệnh đề nào sau đây đúng?

    Đáp án đúng là: \sin(a + b) = \sin a\cos b + \sin b\cos a

  • Câu 3: Vận dụng

    Cho hàm số f(x) = \left\{ \begin{matrix} 2x^{2} + 3x + 30\ \ \ \ khi\ \ x \geq 2 \\ x + 3a + 4\ \ \ \ khi\ \ x \leq 2 \\ \end{matrix} ight.. Khi hàm số liên tục trên \mathbb{R} thì a \in (m;n) ( với m,n là hai số nguyên liên tiếp). Tính 100(m + n).

    Đáp án: 2500

    Đáp án là:

    Cho hàm số f(x) = \left\{ \begin{matrix} 2x^{2} + 3x + 30\ \ \ \ khi\ \ x \geq 2 \\ x + 3a + 4\ \ \ \ khi\ \ x \leq 2 \\ \end{matrix} ight.. Khi hàm số liên tục trên \mathbb{R} thì a \in (m;n) ( với m,n là hai số nguyên liên tiếp). Tính 100(m + n).

    Đáp án: 2500

    TXĐ: D\mathbb{= R}

    Hàm số liên tục khi x eq 2

    Xét tại x = 2

    Ta có: f\left( 2 ight) = 44; \lim_{x ightarrow 2^{+}}f(x) = \lim_{x ightarrow 2^{+}}\left( 2x^{2} + 3x + 30 ight) = 44;\lim_{x ightarrow 2^{-}}f(x) = \lim_{x ightarrow 2^{-}}(x + 3a + 4) = 3a + 6

    Để hàm số liên tục trên \mathbb{R} thì \lim_{x ightarrow 2^{+}}f(x) = \lim_{x ightarrow 2^{-}}f(x) = f(2)

    \Leftrightarrow 3a + 6 = 44 \Leftrightarrow a = \frac{38}{3} \in (12;13)

    \Rightarrow \left\{ \begin{matrix} m = 12 \\ n = 13 \\ \end{matrix} ight.\ \Rightarrow 100(m + n) = 2500

    Đáp án: 2500.

  • Câu 4: Thông hiểu

    \mathop {\lim }\limits_{x \to {1^ - }} \sqrt {\frac{{1 - {x^3}}}{{3{x^2} + x}}} bằng:

    Ta có: \mathop {\lim }\limits_{x \to {1^ - }} \sqrt {\frac{{1 - {x^3}}}{{3{x^2} + x}}} = \mathop {\lim }\limits_{x \to {1^ - }} \sqrt {\frac{{1 - {1^3}}}{{{{3.1}^2} + 1}}} = 0

  • Câu 5: Thông hiểu

    Cho một cấp số cộng (Un) có {u_1} = \frac{1}{3};{u_8} = 26. Công sai d của cấp số cộng là:

    Ta có:

    \begin{matrix} {u_n} = {u_1} + \left( {n - 1} ight)d \hfill \\ \Rightarrow {u_8} = {u_1} + 7d \hfill \\ \Rightarrow 26 = \dfrac{1}{3} + 7.d \hfill \\ \Rightarrow d = \dfrac{{11}}{3} \hfill \\ \end{matrix}

  • Câu 6: Nhận biết

    Cho hàm số y = sinx. Mệnh đề nào sau đây đúng?

    Ta có thể hiểu như sau:

    “ Hàm số y = sinx đồng biến khi góc x thuộc góc phần tư thứ IV và thứ I; nghịch biến khi góc x thuộc góc phần tư thứ II và III”.

  • Câu 7: Vận dụng

    Cho cấp số cộng \left( u_{n} ight) thỏa mãn u_{2} + u_{8} + u_{9} + u_{15} = 100. Tính tổng 16 số hạng đầu tiên của cấp số cộng đã cho.

    Ta có:

    u_{2} + u_{8} + u_{9} + u_{15} = 100

    \Leftrightarrow 4u_{1} + 30d = 100

    \Leftrightarrow 2u_{1} + 15d = 50

    \Rightarrow S_{16} = \frac{16}{2}.\left( u_{1} + u_{16} ight) = 8.50 = 400

  • Câu 8: Nhận biết

    Cho cấp số cộng (u_{n}) có u_{3}=15 và d=-2 . Tìm u_{n} 

    Ta có: 

    \begin{matrix} {u_3} = 15 \hfill \\ \Leftrightarrow {u_1} + 2d = 15 \hfill \\ \Rightarrow {u_1} = 19 \hfill \\ \end{matrix}

    \begin{matrix} \Rightarrow {u_n} = {u_1} + \left( {n - 1} ight).d \hfill \\ = 19 + \left( {n - 1} ight).\left( { - 2} ight) \hfill \\ = 21 - 2n \hfill \\ \Rightarrow {u_n} = - 2n + 21 \hfill \\ \end{matrix}

  • Câu 9: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử (SAB) \cap (SCD) = d. Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Ta có: (SAB) \cap (SCD) = d

    Ta lại có: \left\{ \begin{matrix} S \in (SAB);S \in (SCD) \\ AB \subset (SAB);CD \subset (SCD) \\ AB//CD \\ \end{matrix} ight. suy ra đường thẳng d đi qua S và song song với AB.

  • Câu 10: Nhận biết

    Cho cấp số nhân có số hạng thứ bảy là \frac{1}{2} và công bội \frac{1}{4}. Hỏi số hạng đầu tiên của cấp số nhân bằng bao nhiêu?

    Ta có: \left\{ \begin{matrix}u_{7} = \dfrac{1}{2} = u_{1}.q^{6} \\q = \dfrac{1}{4} \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}u_{1} = 2048 \\q = \dfrac{1}{4} \\\end{matrix} ight.

  • Câu 11: Thông hiểu

    Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là:

    Ta có cấp số nhân (un) nên khi đó:

    \begin{matrix}\left\{ {\begin{array}{*{20}{c}} {{u_m} = 16} \\ {{u_{m + 1}} = 36} \end{array}} ight. \Leftrightarrow \dfrac{{{u_{m + 1}}}}{{{u_m}}} = \dfrac{{36}}{{16}} = \dfrac{9}{4} \Rightarrow q = \dfrac{9}{4} \hfill \\ \Rightarrow {u_{m + 2}} = {u_{m + 1}}.q = 36.\dfrac{9}{4} = 81 \hfill \\ \end{matrix}

  • Câu 12: Nhận biết

    Mệnh đề nào sau đây sai?

    Mệnh đề: “Hình biểu diễn của ba điểm thẳng hàng là một tam giác” sai vì hình biểu diễn phải giữ nguyên tính chất thẳng hàng của 3 điểm.

  • Câu 13: Vận dụng cao

    Có bao nhiêu giá trị nguyên của tham số m để phương trình \sin x. \cos x - \sin x - \cos x + m = 0 có nghiệm:

     Đặt t = \sin x + \cos x;\left( {t \in \left[ { - \sqrt 2 ;\sqrt 2 } ight]} ight)

    => \sin x.\cos x = \frac{{{t^2} - 1}}{2}

    Phương trình trở thành:

    \begin{matrix} \dfrac{{{t^2} - 1}}{2} - t + m = 0 \hfill \\ \Rightarrow - 2m = {t^2} - 2t - 1 \hfill \\ \Rightarrow {\left( {t - 1} ight)^2} = - 2m + 2 \hfill \\ \end{matrix}

    Do  {t \in \left[ { - \sqrt 2 ;\sqrt 2 } ight]}

    \begin{matrix} \Leftrightarrow - \sqrt 2 - 1 \leqslant t - 1 \leqslant \sqrt 2 - 1 \hfill \\ \Leftrightarrow 0 \leqslant {\left( {t - 1} ight)^2} \leqslant 3 + 2\sqrt 2 \hfill \\ \end{matrix}

    Vậy để phương trình có nghiệm

    \begin{matrix} \Leftrightarrow 0 \leqslant - 2m + 2 \leqslant 3 + 2\sqrt 2 \hfill \\ \Leftrightarrow - \dfrac{{1 + 2\sqrt 2 }}{2} \leqslant m \leqslant 1 \hfill \\ m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} ight\} \hfill \\ \end{matrix}

  • Câu 14: Thông hiểu

    Giả sử tứ giác ABCD là hình biểu diễn của một hình vuông. Nếu ABCD là một hình bình hành, thì đường tròn ngoại tiếp hình vuông cho trước được biểu diễn là hình gì, có tính chất như thế nào với hình bình hành ABCD:

    Hình biểu diễn của hình vuông thành hình bình hành nên sẽ hình biểu diễn của đường tròn ngoại tiếp hình vuông đó là đường elip đồng thời giữ nguyên mối quan hệ liên thuộc của đỉnh hình vuông với đường tròn ngoại tiếp nên hình biểu diễn của đường tròn ngoại tiếp hình vuông là đường elip đi qua các đỉnh của hình bình hành ABCD.

  • Câu 15: Nhận biết

    Cho dãy số (un) với \left\{ \begin{matrix} u_{1} = 1 \\ u_{n + 1} = u_{n} + ( - 1)^{2n} \\ \end{matrix} ight.. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?

    Ta có un + 1 = un + (−1)2n = un + 1 ⇒ u2 = 2; u3 = 3; u4 = 4; …

    Dễ dàng dự đoán được un = n.

    Thật vậy, ta chứng minh được un = n (*) bằng phương pháp quy nạp như sau:

    Với n = 1 ⇒ u1 = 1. Vậy (*) đúng với n = 1.

    Giả sử (*) đúng với n = k (k∈ℕ*), ta có uk = k

    Ta đi chứng minh (*) cũng đúng với n = k + 1, tức là uk + 1 = k + 1

    Thật vậy, từ hệ thức xác định dãy số (un) ta có uk + 1 = uk + (−1)2k = k + 1

    Vậy (*) đúng với mọi n ∈ ℕ*. Số hạng tổng quát của dãy số là un = n.

  • Câu 16: Nhận biết

    Hình chóp ngũ giác có bao nhiêu cạnh?

    Hình chóp ngũ giác có 10 cạnh.

  • Câu 17: Nhận biết

    Cho cấp số nhân \left( u_{n} ight) với u_{1} = 3 và u_{2} = 12. Công bội của cấp số nhân đã cho bằng

    Ta có u_{2} = u_{1}.q \Rightarrow q = \frac{u_{2}}{u_{1}} = \frac{12}{3} = 4.

  • Câu 18: Vận dụng

    Giá trị lớn nhất của hàm số y = \frac{\sin x + 2\cos x + 1}{\sin x + \cos x +2} tại điểm là nghiệm của phương trình nào dưới đây?

    Theo bài ra ta có:

    y = \frac{\sin x + 2\cos x + 1}{\sin x + \cos x +2}

    \Leftrightarrow y.\left( \sin x + \cos x+ 2 ight) = \sin x + 2\cos x + 1

    \Leftrightarrow (y - 1).\sin x + (y -2)\cos x = 1 - 2y(*)

    Phương trình (*) có nghiệm

    \Leftrightarrow (y - 1)^{2} + (y - 2)^{2} \geq 1 - 2y

    \Leftrightarrow y^{2} + y - 2 \leq 0

    \Leftrightarrow - 2 \leq y \leq 1

    Vậy giá trị lớn nhất của hàm số bằng 1 lúc đó - \cos x = - 1

  • Câu 19: Thông hiểu

    Tìm chu kì T của hàm số y = - \frac{1}{2}\sin \left( {100\pi x + 50\pi } ight)

    Hàm số y = - \frac{1}{2}\sin \left( {100\pi x + 50\pi } ight) tuần hoàn với chu kì T = \frac{{2\pi }}{{100\pi }} = \frac{1}{{50}}.

  • Câu 20: Nhận biết

    Cho tứ diện ABCD, G là trọng tâm tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB = 2MC. Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Vì MG//CD nên MG // ( ACD ).

  • Câu 21: Vận dụng cao

    Cho các số thực a,b,c thỏa mãn \left\{ \begin{matrix} - 8 + 4a - 2b + c > 0 \\ 8 + 4a + 2b + c < 0 \\ \end{matrix} ight.. Khi đó số giao điểm của hàm số y = x^{3} + ax^{2} + bx + c với trục Ox là:

    Hàm số y = x^{3} + ax^{2} + bx + c xác định và liên tục trên \mathbb{R}.

    Hàm số y = x^{3} + ax^{2} + bx + c bậc ba nên đồ thị hàm số cắt Ox tối đa tại 3 điểm (1)

    Ta có:

    \lim_{x ightarrow - \infty}y = - \infty suy ra \exists\alpha < - 2 sao cho f(\alpha) < 0

    Lại có: \lim_{x ightarrow + \infty}y = + \infty suy ra \exists\beta > 2 sao cho f(\beta) > 0

    Mặt khác \left\{ \begin{matrix} y( - 2) = - 8 + 4a - 2b + c > 0 \\ y(2) = 8 + 4a + 2b + c < 0 \\ \end{matrix} ight.

    Từ đó suy ra \left\{ \begin{matrix} y(\alpha).y( - 2) < 0 \\ y( - 2).y(2) < 0 \\ y(2).y(\beta) < 0 \\ \end{matrix} ight.

    Do đó đồ thị hàm số cắt Ox tại ít nhất ba điểm (2)

    Từ (1) và (2) suy ra đồ thị hàm số đã cho cắt trục Ox tại đúng ba điểm.

  • Câu 22: Thông hiểu

    Cho dãy số (un) biết u_{n} = \frac{5^{n}}{n^{2}}. Mệnh đề nào sau đây đúng?

    Ta có u_{n} = \frac{5^{n}}{n^{2}} > 0,\forall n \in \mathbb{N}^{*} \Rightarrow u_{n + 1} = \frac{5^{n + 1}}{(n + 1)^{2}}

    Xét tỉ số:

    \frac{u_{n + 1}}{u_{n}} = \frac{5^{n + 1}}{(n + 1)^{2}} \cdot \frac{n^{2}}{5^{n}}

    = \frac{5n^{2}}{n^{2} + 2n + 1} = \frac{n^{2} + 2n + 1 + 4n^{2} - 2n - 1}{n^{2} + 2n + 1}

    = 1 + \frac{2n(n - 1) + 2n^{2} - 1}{n^{2} + 2n + 1} > 1,\forall n \in \mathbb{N}^{*}

    Vậy (un) là dãy số tăng.

  • Câu 23: Thông hiểu

    Cho tứ diện ABCD, lấy M,N lần lượt là trung điểm của BC và CD. Giả sử d = (MNA) \cap (ABD). Khẳng định nào đúng về đặc điểm của đường thẳng d?

    Hình vẽ minh họa

    Xét ba mặt phẳng (AMN),(ABD),(BCD)

    Ba mặt phẳng này đôi một cắt nhau theo ba giao tuyến là d,BD,MN.

    Theo định lí về giao tuyến của ba mặt phẳng thì d,BD,MN đồng quy hoặc đôi một song song.

    Mà BD//MN nên d//BD.

    Vậy đường thẳng d đi qua A và song song với BD.

  • Câu 24: Nhận biết

    Giá trị của \lim\sqrt[n]{a} với a> 0 bằng:

    Nếu a=1 thì ta có luôn giới hạn bằng 1.

    • Với  a > 1 thì khi đó: a = \left\lbrack 1 +\left( \sqrt[n]{a} - 1 ight) ightbrack^{n} > n(\sqrt[n]{a} -1)

    Suy ra: 0 < \sqrt[n]{a - 1} <\frac{a}{n} ightarrow 0 nên \lim\sqrt[n]{a} = 1

    • Với 0 < a < 1 thì khi đó:  \frac{1}{a} >1 .

    Suy ra: \lim \sqrt[n]{\frac{1}{a} }=1 \Rightarrow \lim \sqrt[n]{a}=1.\frac{1}{a}>1 \Rightarrow \lim \sqrt[n]{a}=1

    Tóm lại ta luôn có: \lim\sqrt[n]{a} =1 với a > 0 .

  • Câu 25: Vận dụng

    Cho cấp số nhân (un) có \left\{ {\begin{array}{*{20}{c}} {{u_{20}} = 8{u_{17}}} \\ {{u_1} + {u_5} = 272} \end{array}} ight.. Tìm số hạng đầu tiên của dãy biết số đó không lớn hơn 100.

     Ta có: 

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {{u_{20}} = 8{u_{17}}} \\ {{u_1} + {u_5} = 272} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{u_1}{q^{19}} = 8{u_1}.{q^{16}}} \\ {{u_1} + {u_1}.{q^4} = 272} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{u_1}{q^{16}}\left( {{q^3} - 8} ight) = 0} \\ {{u_1}.\left( {1 + {q^4}} ight) = 272} \end{array}} ight. \hfill \\ \Rightarrow \left[ {\begin{array}{*{20}{c}} {q = 0 \Rightarrow {u_1} = 272 > 100\left( L ight)} \\ {q = 2 \Rightarrow {u_1} = 16 < 100\left( {tm} ight)} \end{array}} ight. \hfill \\ \end{matrix}

  • Câu 26: Thông hiểu

    Tất cả các nghiệm của phương trình tan (x) = cot (x) là?

     Điều kiện \left\{ \begin{gathered} \sin x e 0 \hfill \\ \cos x e 0 \hfill \\ \end{gathered} ight.\, \Leftrightarrow \sin 2x e 0\, \Leftrightarrow x e m\frac{\pi }{2}\,{\text{ , }}m \in \mathbb{Z}

    \tan x = \cot x \Leftrightarrow \tan x = \tan \left( {\frac{\pi }{2} - x} ight)

    \Leftrightarrow x = \frac{\pi }{2} - x + k\pi

    \Leftrightarrow x = \frac{\pi }{4} + k\frac{\pi }{2}\,\,\,\left( {\,k \in \mathbb{Z}} ight) thỏa mãn điều kiện.

  • Câu 27: Thông hiểu

    Nhận định sự đúng sai của các kết luận sau?

    a) \lim_{x ightarrow 1}\frac{3x + 2}{2 - x} = 5 . Đúng||Sai

    b) Phương trình x^{3} - 3x^{2} + 3 = 0 có đúng 3 nghiệm phân biệt. Đúng||Sai

    c) Nếu \lim_{x ightarrow 0}f(x) = 5 thì \lim_{x ightarrow 0}\left\lbrack 3x - 4f(x) ightbrack bằng - 15. Sai||Đúng

    d) Hàm số f(x) = \left\{ \begin{matrix}\dfrac{\sqrt{1 + 2x} - 1}{x}\ \ \ khi\ x\ > \ 0 \\1 + 3x\ \ \ \ \ \ \ \ \ khi\ x \leq 0 \\\end{matrix} ight. gián đoạn tại x = 0. Sai||Đúng

    Đáp án là:

    Nhận định sự đúng sai của các kết luận sau?

    a) \lim_{x ightarrow 1}\frac{3x + 2}{2 - x} = 5 . Đúng||Sai

    b) Phương trình x^{3} - 3x^{2} + 3 = 0 có đúng 3 nghiệm phân biệt. Đúng||Sai

    c) Nếu \lim_{x ightarrow 0}f(x) = 5 thì \lim_{x ightarrow 0}\left\lbrack 3x - 4f(x) ightbrack bằng - 15. Sai||Đúng

    d) Hàm số f(x) = \left\{ \begin{matrix}\dfrac{\sqrt{1 + 2x} - 1}{x}\ \ \ khi\ x\ > \ 0 \\1 + 3x\ \ \ \ \ \ \ \ \ khi\ x \leq 0 \\\end{matrix} ight. gián đoạn tại x = 0. Sai||Đúng

    Ta có: \lim_{x ightarrow 1}\frac{3x + 2}{2 - x} = \frac{3.1 + 2}{3 - 1} = 5

    Xét phương trình x^{2} - 3x^{2} + 3 = 0. Đặt x^{2} - 3x^{2} + 3 = f(x) là hàm số liên tục trên \mathbb{R} suy ra hàm số cũng liên tục trên \lbrack - 1;3brack.

    Ta có: f( - 1) = - 1;f(1) = 1;f(2) = - 1;f(3) = 3

    Khi đó: \left\{ \begin{matrix} f( - 1).f(1) < 0 \\ f(1).f(2) < 0 \\ f(2).f(3) < 0 \\ \end{matrix} ight. nên phương trình f(x) = 0 có ít nhất 3 nghiệm

    f(x) = 0 là phương trình bậc 3 có tối đa 3 nghiệm

    Vậy phương trình đã cho có đúng 3 nghiệm.

    Ta có:

    Nếu \lim_{x ightarrow 0}f(x) = 5 suy ra

    \lim_{x ightarrow 0}\left\lbrack 3x - 4f(x) ightbrack

    = \lim_{x ightarrow 0}(3x) - 4\lim_{x ightarrow 0}f(x) = 3.0 - 4.5 = - 20

    Ta có:

    \lim_{x ightarrow 0^{+}}\frac{\sqrt{1 + 2x} - 1}{x} = \lim_{x ightarrow 0^{+}}\frac{\left( \sqrt{1 + 2x} - 1 ight)\left( \sqrt{1 + 2x} + 1 ight)}{x\left( \sqrt{1 + 2x} + 1 ight)}

    = \lim_{x ightarrow 0^{+}}\frac{2}{\sqrt{1 + 2x} + 1} = 1

    \lim_{x ightarrow 0^{-}}f(x) = \lim_{x ightarrow 0^{-}}(1 + 3x) = 1

    Vậy hàm số đã cho liên tục tại x = 0.

  • Câu 28: Vận dụng cao

    Cho hình lập phương ABCD.A'B'C'D' cạnh a. Mặt phẳng (\alpha) đi qua tâm của hình lập phương và song song với (ABC). Xác định các giao tuyến của mặt phẳng (\alpha) và tứ diện AB'CD'. Hình tạo bởi các giao tuyến đó có diện tích bằng bao nhiêu?

    Hình vẽ minh họa:

    Gọi I là tâm của hình lập phương

    => I là trung điểm của AC’.

    Gọi (P) là mặt phẳng qua I và song song với (ABC).

    Khi đó (P) cắt các đường thẳng AB’, B’C, CD’, AD’ lần lượt tại các trung điểm M, N, P, Q.

    Khi đó \left\{ \begin{matrix}MN = QP = \dfrac{1}{2}AC = \dfrac{a\sqrt{2}}{2} \\NP = MQ = \dfrac{1}{2}B'D' = \dfrac{a\sqrt{2}}{2} \\\end{matrix} ight.

    => Hình tạo bởi các giao tuyến của mặt phẳng (\alpha) và tứ diện AB'CD' là hình thoi MNPQ cạnh bằng \frac{a\sqrt{2}}{2}

    Mặt khác NQ = MP = BC = a

    Diện tích hình thoi MNPQ là S = \frac{1}{2}NQ.MP = \frac{a^{2}}{2}

  • Câu 29: Vận dụng

    Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của MA và SD.

    Hình vẽ minh họa:

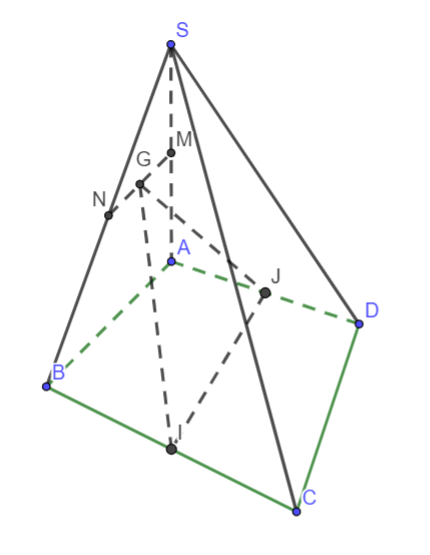
    Tìm giao tuyến của MA và SD

    Xét hình thang ABCD có I và J lần lượt là trung điểm của AD; BC nên:

    IJ là đường trung bình hình thang ABCD => IJ // AB

    Hai mặt phẳng (GIJ) và (SAB): lần lượt chứa hai đường thẳng song song (là IJ và AB) và có điểm G chung

    => Giao tuyến của chúng là đường thẳng đi qua G và song song với AB.

    Đường thẳng này cắt SA tại M và cắt SB tại N.

  • Câu 30: Nhận biết

    Cho hàm số f(x) xác định trên tập số thực và có đồ thị như hình vẽ:

    Hỏi hàm số f(x) không liên tục tại điểm nào sau đây?

    Quan sát đồ thị hàm số ta thấy: \left\{ \begin{matrix} \lim_{x ightarrow 1^{-}}f(x) = 3 \\ \lim_{x ightarrow 1^{+}}f(x) = 0 \\ \end{matrix} ight.

    Vậy \lim_{x ightarrow 1^{-}}f(x) eq \lim_{x ightarrow 1^{+}}f(x) nên không tồn tại \lim_{x ightarrow 1}f(x). Do đó hàm số gián đoạn tại x_{0} = 1.

  • Câu 31: Vận dụng cao

    Tổng S = sin(x) + sin(2x) + … + sin(nx) (với x ≠ kπ ) có công thức thu gọn là?

    Ta có 2sin\frac{x}{2} \cdot S = 2sinx\cdot sin\frac{x}{2} + 2sin2x \cdot sin\frac{x}{2} + .. + 2sinnx \cdotsin\frac{x}{2}

    = \cos\frac{x}{2} - \cos\frac{3x}{2} +\cos\frac{3x}{2} - \cos{x\frac{5x}{2}} + \ldots + \cos{x\frac{2n -1}{2}x} - \cos{\frac{2n + 1}{2}x}

    = cos\frac{x}{2} - cos\frac{2n +1}{2}x

    Vậy S = \frac{cos\frac{x}{2} - cos\frac{2n+ 1}{2}x}{2sin\frac{x}{2}}

  • Câu 32: Vận dụng

    Cho tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều các cạnh tương ứng thành các phần bằng nhau. Hỏi có bao nhiêu tam giác được tạo thành mà có 3 đỉnh lấy từ 18 điểm đã đánh dấu sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho?

    Đáp án: 216

    Đáp án là:

    Cho tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều các cạnh tương ứng thành các phần bằng nhau. Hỏi có bao nhiêu tam giác được tạo thành mà có 3 đỉnh lấy từ 18 điểm đã đánh dấu sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho?

    Đáp án: 216

    Hình vẽ minh họa

    Không mất tính tổng quát, xét mặt bên \Delta ABC.

    Giả sử MN song song với BC. Khi đó, số tam giác có cạnh MN nằm trong mặt phẳng song song với đúng một cạnh của tứ diện là 6 tam giác, gồm \Delta PMN, \Delta QMN, \Delta IMN,\Delta JMN, \Delta KMN, \Delta LMN.

    Trong mặt bên \Delta ABC, nối các điểm chia đều các cạnh AB,BC,CA ta thấy có 3 đoạn thẳng song song với AB, 3 đoạn thẳng song song với BC và 3 đoạn thẳng song song với CA.

    Mặt khác, vai trò 4 mặt của tứ diện là như nhau.

    Vậy, số tam giác thỏa mãn yêu cầu đề bài là 6.(3 + 3 + 3).4 = 216.

  • Câu 33: Nhận biết

    Chọn khẳng định đúng.

    Ta có: \pi rad tương ứng với 180^{0}.

  • Câu 34: Thông hiểu

    Có bao nhiêu mặt phẳng đi qua 3 điểm không thẳng hàng?

    Có duy nhất 1 mặt phẳng đi qua ba điểm không thẳng hàng.

  • Câu 35: Vận dụng cao

    Kết quả của giới hạn\lim\frac{2^{n + 1} + 3n + 10}{3n^{2} - n + 2} là:

    Ta có:

    \begin{matrix} {2^n} = \sum\limits_{k = 0}^n {C_n^k} \hfill \\ \Rightarrow {2^n} \geqslant C_n^3 = \dfrac{{n\left( {n - 1} ight)\left( {n - 2} ight)}}{6} \sim \dfrac{{{n^3}}}{6} \hfill \\ \end{matrix}

    \Rightarrow \left\{ \begin{matrix}\dfrac{n}{2^{n}} ightarrow 0 \\\dfrac{2^{n}}{n^{2}} ightarrow + \infty \\\end{matrix} ight.

    Khi đó:

    \begin{matrix} \lim \dfrac{{{2^{n + 1}} + 3n + 10}}{{3{n^2} - n + 2}} \hfill \\ = \lim \dfrac{{{2^n}}}{{{n^2}}}.\dfrac{{2 + 3.\dfrac{n}{{{2^n}}} + 10.{{\left( {\dfrac{1}{2}} ight)}^n}}}{{3 - \dfrac{1}{n} + \dfrac{2}{{{n^2}}}}} \hfill \\ \end{matrix}

    Vì \left\{ \begin{matrix}\lim\dfrac{2^{n}}{n^{2}} = + \infty \\\lim\dfrac{2 + 3.\dfrac{n}{2^{n}} + 10.\left( \dfrac{1}{2} ight)^{n}}{3 -\dfrac{1}{n} + \dfrac{2}{n^{2}}} = \dfrac{2}{3} > 0 \\\end{matrix} ight.

    Vậy \lim\dfrac{2^{n + 1} + 3n + 10}{3n^{2}- n + 2} = + \infty

  • Câu 36: Thông hiểu

    Kiểm tra sự đúng sai của các kết luận sau?

    a) Có hai trong ba hàm số y = \sin;y =\cos\sqrt{x};y = \tan x liên tục trên tập số thực. Sai||Đúng

    b) \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = - 1 Đúng||Sai

    c) Phương trình 2x^{4} - 5x^{2} + x + 1 = 0 có ít nhất hai nghiệm thuộc khoảng (0;2).Đúng||Sai

    d) Biết hàm số f\left( x ight) = \left\{ \begin{gathered} \dfrac{{{x^2} + 1}}{{1 - x}}{\text{ khi x < 1}} \hfill \\ \sqrt {2x - 2} {\text{ khi x}} \geqslant {\text{1}} \hfill \\ \end{gathered} ight.. Khi đó \lim_{x ightarrow 1^{-}}f(x) = - \infty. Sai||Đúng

    Đáp án là:

    Kiểm tra sự đúng sai của các kết luận sau?

    a) Có hai trong ba hàm số y = \sin;y =\cos\sqrt{x};y = \tan x liên tục trên tập số thực. Sai||Đúng

    b) \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = - 1 Đúng||Sai

    c) Phương trình 2x^{4} - 5x^{2} + x + 1 = 0 có ít nhất hai nghiệm thuộc khoảng (0;2).Đúng||Sai

    d) Biết hàm số f\left( x ight) = \left\{ \begin{gathered} \dfrac{{{x^2} + 1}}{{1 - x}}{\text{ khi x < 1}} \hfill \\ \sqrt {2x - 2} {\text{ khi x}} \geqslant {\text{1}} \hfill \\ \end{gathered} ight.. Khi đó \lim_{x ightarrow 1^{-}}f(x) = - \infty. Sai||Đúng

    a) Ta có hàm số lượng giác liên tục trên từng khoảng xác định của nó.

    Hàm số y = \sin xác định trên tập số thực suy ra hàm số liên tục trên \mathbb{R}

    Hàm số y = \cos\sqrt{x} xác định trên D = \lbrack 0; + \infty)

    Hàm sốy = \tan x xác định trên D\mathbb{= R}\backslash\left\{ \frac{\pi}{2} + k\pi|k\mathbb{\in Z} ight\}

    Vậy chỉ có suy nhất một hàm số liên tục trên tập số thực.

    b) Ta có:

    \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x ight) - \lim_{x ightarrow - \infty}1

    = \lim_{x ightarrow - \infty}\left( \frac{1}{\sqrt{x^{2} + 1} - x} ight) - 1 = \lim_{x ightarrow - \infty}\left( \frac{\frac{1}{x}}{- \sqrt{1 + \frac{1}{x}} - 1} ight) - 1 = - 1

    c) Xét hàm số 2x^{4} - 5x^{2} + x + 1 = f(x) liên tục trên \mathbb{R}

    Ta có: \left\{ \begin{matrix} f( - 2) = 11;f( - 1) = - 3 \\ f(0) = 1;f(1) = - 1;f(2) = 15 \\ \end{matrix} ight.

    Vì \left\{ \begin{matrix} f(0).f( - 1) < 0 \\ f(1).f(2) < 0 \\ \end{matrix} ight. nên phương trình đã cho có ít nhất hai nghiệm thuộc khoảng (0;2).

    d) Ta có: \left\{ \begin{matrix} \lim_{x ightarrow 1^{-}}\left( x^{2} + 1 ight) = 2 > 0 \\ \lim_{x ightarrow 1^{-}}(1 - x) = 0 \\ \end{matrix} ight.. Khi x ightarrow 1^{-} \Leftrightarrow x < 1 \Leftrightarrow 1 - x > 0

    \lim_{x ightarrow 1^{-}}f(x) = \lim_{x ightarrow 1^{-}}\frac{x^{2} + 1}{1 - x} = + \infty.

  • Câu 37: Vận dụng

    \lim_{x ightarrow 1}\frac{x^{100} - 2x + 1}{x^{50} - 2x + 1} bằng:

    Ta có:

    \lim_{x ightarrow 1}\frac{x^{100} - 2x + 1}{x^{50} - 2x + 1}

    = \lim_{x ightarrow 1}\frac{\left( x^{100} - 1 ight) - 2(x - 1)}{\left( x^{50} - 1 ight) - 2(x - 1)}

    = \lim_{x ightarrow 1}\frac{(x - 1)\left( x^{99} + x^{98} + .... + x + 1 - 2 ight)}{(x - 1)\left( x^{49} + x^{48} + .... + x + 1 - 2 ight)}

    = \lim_{x ightarrow 1}\frac{x^{99} + x^{98} + .... + x + 1 - 2}{x^{49} + x^{48} + .... + x + 1 - 2} = \frac{98}{48} = \frac{49}{24}

  • Câu 38: Thông hiểu

    Tính giá trị của biểu thức C = \dfrac{\sin\dfrac{5\pi}{18}.\cos\dfrac{\pi}{9} -\sin\dfrac{\pi}{9}.\cos\dfrac{5\pi}{18}}{\cos\dfrac{\pi}{4}.\cos\dfrac{\pi}{12}- \sin\dfrac{\pi}{4}.\sin\dfrac{\pi}{12}} là:

    Ta có:

    \sin\dfrac{5\pi}{18}.\cos\dfrac{\pi}{9} -\sin\dfrac{\pi}{9}.\cos\dfrac{5\pi}{18}

    = \sin\left( \frac{5\pi}{18} -\frac{\pi}{9} ight)

    = \sin\frac{\pi}{6} =\frac{1}{2}

    \cos\dfrac{\pi}{4}.\cos\dfrac{\pi}{12} -\sin\dfrac{\pi}{4}.\sin\frac{\pi}{12}

    = \cos\left( \frac{\pi}{4} +\frac{\pi}{12} ight)

    = \cos\frac{\pi}{3} =\frac{1}{2}

    Vậy C=1

  • Câu 39: Thông hiểu

    Cho cấp số cộng (Un) có u_1=11 và công sai d = 4. Tính {u_{99}}?

    Ta có: {u_{99}} = {u_1} + 99d = 11 + 98.4 = 403

  • Câu 40: Nhận biết

    Cho hàm số y = f(x) = \frac{2x + 3}{x - 1}. Tính \lim_{x ightarrow - \infty}f(x).

    Hàm số đã cho xác định trên ( - \infty;1) và (1; + \infty)

    Giả sử \left( x_{n} ight) là một dãy số bất kì, thỏa mãn x_{n} < 1;x_{n} ightarrow - \infty

    Ta có: \lim f\left( x_{n} ight) =\lim\dfrac{2x_{n} + 3}{x_{n} - 1} = \lim\dfrac{2 + \dfrac{3}{x_{n}}}{1 -\dfrac{1}{x_{n}}} = 2

    Vậy \lim_{x ightarrow - \infty}\frac{2x + 3}{x - 1} = 2

  • Câu 41: Nhận biết

    Khẳng định nào sau đây là đúng?

    Khẳng định đúng là: "Cho hai mặt phẳng (P), (Q) song song. Khi đó nếu đường thẳng a không nằm trong mặt phẳng (Q) và a song song với (P) thì a song song với (Q)."

  • Câu 42: Nhận biết

    Phương trình \tan x = \tan 3x có nghiệm là:

     Giải phương trình:

    \begin{matrix} \tan x = \tan 3x \hfill \\ \Leftrightarrow \tan 3x = \tan x \hfill \\ \Leftrightarrow 3x = x + k\pi \hfill \\ \Leftrightarrow 2x = k\pi \hfill \\ \Leftrightarrow x = \dfrac{{k\pi }}{2};\left( {k \in \mathbb{Z}} ight) \hfill \\ \end{matrix}

  • Câu 43: Thông hiểu

    Tìm nghiệm dương nhỏ nhất của phương trình 2\sin \left( {4x - \frac{\pi }{3}} ight) - 1 = 0.

     Ta có 2\sin \left( {4x - \frac{\pi }{3}} ight) - 1 = 0 \Leftrightarrow \sin \left( {4x - \frac{\pi }{3}} ight) = \frac{1}{2}

    \Leftrightarrow \sin \left( {4x - \frac{\pi }{3}} ight) = \sin \frac{\pi }{6}

    \Leftrightarrow \left[ \begin{gathered} 4x - \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \hfill \\ 4x - \frac{\pi }{3} = \pi - \frac{\pi }{6} + k2\pi \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} 4x = \frac{\pi }{2} + k2\pi \hfill \\ 4x = \frac{{7\pi }}{6} + k2\pi \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{8} + \frac{{k\pi }}{2} \hfill \\ x = \frac{{7\pi }}{{24}} + \frac{{k\pi }}{2} \hfill \\ \end{gathered} ight.{\text{ }}\left( {k \in \mathbb{Z}} ight).

    TH1. Với x = \frac{\pi }{8} + \frac{{k\pi }}{2}\xrightarrow{{{\text{Cho}} > 0}}\frac{\pi }{8} + \frac{{k\pi }}{2} > 0

    \Leftrightarrow k > - \frac{1}{4} \to {k_{\min }} = 0 \Rightarrow x = \frac{\pi }{8}

    TH2. Với x = \frac{{7\pi }}{{24}} + \frac{{k\pi }}{2}\xrightarrow{{{\text{Cho}} > 0}}\frac{{7\pi }}{{24}} + \frac{{k\pi }}{2} > 0

    \Leftrightarrow k > - \frac{7}{{12}} \to {k_{\min }} = 0 \Rightarrow x = \frac{{7\pi }}{{24}}

    So sánh hai nghiệm ta được x = \frac{\pi }{8} là nghiệm dương nhỏ nhất.

  • Câu 44: Nhận biết

    Cho dãy số \left( u_{n} ight) với u_{n} = \frac{4^{n - 1}}{5^{n - 2}}. Tính \lim_{n ightarrow + \infty}u_{n}.

    Ta có:

    \lim_{n ightarrow + \infty}u_{n} = \lim_{n ightarrow + \infty}\frac{4^{n - 1}}{5^{n - 2}} = \lim_{n ightarrow + \infty}\left( \left( \frac{4}{5} ight)^{n}.\frac{4^{- 1}}{5^{- 2}} ight) = 0

  • Câu 45: Thông hiểu

    Chọn mệnh đề sai trong các mệnh đề sau:

    Nếu hình chiếu song song của hai đường thẳng là một đường thẳng thì hai đường thẳng đó phải nằm trong một mặt phẳng song song hoặc chứa phương chiếu.

    Mặt khác hai đường thẳng chéo nhau không cùng nằm trong bất kì mặt phẳng nào.

    Do đó mệnh đề sai là: “Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.”.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 11 Cánh Diều Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 53 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 11 Cánh Diều Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập