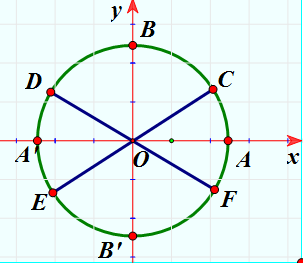
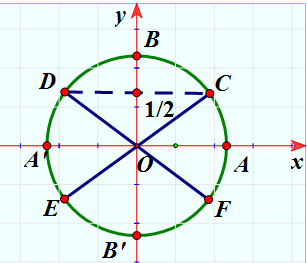
Xét đường tròn lượng giác như hình vẽ. Biết ![]() , E và D lần lượt là các điểm đối xứng của C và F qua gốc O. Nghiệm của phương trình
, E và D lần lượt là các điểm đối xứng của C và F qua gốc O. Nghiệm của phương trình ![]() được biểu diễn trên đường tròn lượng giác là những điểm nào?
được biểu diễn trên đường tròn lượng giác là những điểm nào?
Ta có:
Dựa vào đường tròn lượng giác ta có điểm biểu diễn nghiệm của phương trình là điểm C và điểm D.








 liên tục tại
liên tục tại 