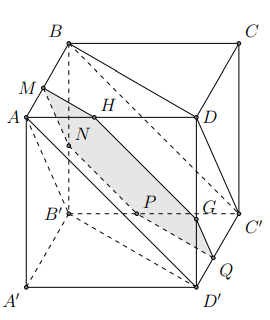
Cho hình chóp ![]() có đáy
có đáy ![]() là hình thang
là hình thang ![]() . Gọi
. Gọi ![]() lần lượt là các điểm thuộc các cạnh
lần lượt là các điểm thuộc các cạnh ![]() thỏa mãn
thỏa mãn ![]()
![]() . Biết
. Biết ![]() và
và ![]() là trung điểm của
là trung điểm của ![]() . Phân tích sự đúng sai của các phát biểu dưới đây?
. Phân tích sự đúng sai của các phát biểu dưới đây?
a) ![]() Đúng||Sai
Đúng||Sai
b) ![]() Đúng||Sai
Đúng||Sai
c) ![]() Đúng||Sai
Đúng||Sai
d) Thiết diện tạo bởi mặt phẳng ![]() và mặt phẳng
và mặt phẳng ![]() là một hình thang. Sai||Đúng
là một hình thang. Sai||Đúng
Cho hình chóp có đáy
là hình thang
. Gọi
lần lượt là các điểm thuộc các cạnh
thỏa mãn
. Biết
và
là trung điểm của
. Phân tích sự đúng sai của các phát biểu dưới đây?
a) Đúng||Sai
b) Đúng||Sai
c) Đúng||Sai
d) Thiết diện tạo bởi mặt phẳng và mặt phẳng
là một hình thang. Sai||Đúng
Hình vẽ minh họa
Xét tam giác DBC có
Xét tam giác ABC có:
Suy ra ba điểm O; K; J thẳng hàng
Suy ra đúng
Tương tự ta cũng chúng minh được (Vì
)
Suy ra
Gọi F là trung điểm của SA khi đó
Mà tứ giác CDEF là hình bình hành nên CE // DF. Từ đó suy ra IH // CE.
Ta lại có: IJKH là thiết diện của hình chóp S.ABCD và (IJK) và nó không là hình thang.