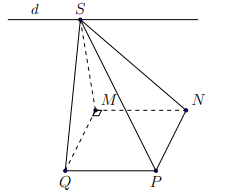Cho hình chóp ![]() có đáy là hình bình hành. Qua
có đáy là hình bình hành. Qua ![]() kẻ
kẻ ![]() lần lượt song song với
lần lượt song song với ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Các mệnh đề sau đúng hay sai?
. Các mệnh đề sau đúng hay sai?
a) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
b) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
c) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Đúng||Sai
. Đúng||Sai
d) Giao tuyến của ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() . Sai||Đúng
. Sai||Đúng
Cho hình chóp có đáy là hình bình hành. Qua
kẻ
lần lượt song song với
. Gọi
là giao điểm của
và
. Các mệnh đề sau đúng hay sai?
a) Giao tuyến của và
là đường thẳng
. Sai||Đúng
b) Giao tuyến của và
là đường thẳng
. Sai||Đúng
c) Giao tuyến của và
là đường thẳng
. Đúng||Sai
d) Giao tuyến của và
là đường thẳng
. Sai||Đúng
Hình vẽ minh họa
Ta có:
với
.
Kết luận:
|
a) Sai |
b) Sai |
c) Đúng |
d) Sai |








 . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?