Có bao nhiêu giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() ?
?
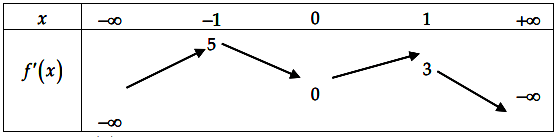
Đặt
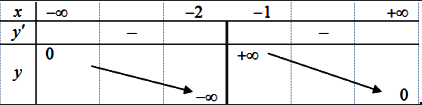
Khi đó hàm số đã cho đồng biến trên khoảng khi và chỉ khi hàm số
đồng biến trên khoảng
Hàm số đồng biến trên khoảng
khi và chỉ khi:
Vì
Vậy có tất cả 2020 số nguyên m thỏa mãn yêu cầu bài toán.








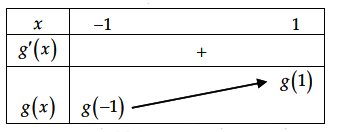
 với x > 1 và a + b = 2. Tính giá trị của biểu thức
với x > 1 và a + b = 2. Tính giá trị của biểu thức