Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 1

Mô tả thêm: Đề kiểm tra học kì 2 Toán 10 được biên soạn gồm 40 câu hỏi trắc nghiệm chia thành 4 mức độ bám sát chương trình sách Chân trời sáng tạo.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:\left\{ \begin{matrix} x = 1 - 4t \\ y = - 2 + 3t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight). Hãy chỉ ra vectơ chỉ phương của đường thẳng d?

    Vectơ chỉ phương của đường thẳng dlà: \overrightarrow{u_{d}} = ( - 4;3).

  • Câu 2: Nhận biết

    Xét một phép thử T và không gian mẫu là \Omega. Giả sử C là một biến cố liên quan đến phép thử. Xác suất của biến cố C là:

    Công thức đúng là: P(C) = \frac{n(C)}{n(\Omega)}.

  • Câu 4: Nhận biết

    Cho phương trình x^{2} + y^{2} + 2mx + 2(m–1)y + 2m^{2} = 0(1). Tìm điều kiện của m để (1) là phương trình đường tròn.

    Ta có: x^{2} + y^{2} + 2mx + 2(m–1)y + 2m^{2} = 0

    ightarrow \left\{ \begin{matrix} a = - m \\ b = 1 - m \\ c = 2m^{2} \\ \end{matrix} ight.\ ightarrow a^{2} + b^{2} - c > 0 \Leftrightarrow - 2m + 1 > 0 \Leftrightarrow m < \frac{1}{2}.

  • Câu 5: Nhận biết

    Phương trình đường tròn (C) có tâm I( - 1;2) và bán kinh R = 6 là:

    Ta có: (C):\left\{ \begin{matrix} I( - 1;2) \\ R = 6 \\ \end{matrix} ight.\ \Rightarrow (C):(x + 1)^{2} + (y - 2)^{2} = 36

  • Câu 6: Thông hiểu

    Cho đường tròn (C) có tâm I thuộc đường thẳng d_{1}:x - y + 1 = 0 có bán kính R = 2 và cắt đường thẳng d_{2}:3x - 4y = 0 tại hai điểm A;B sao cho AB = 2\sqrt{3}. Phương trình đường tròn (C) cần tìm là:

    Gọi tâm I thuộc đường thẳng d_{1} nên suy ra I(a;a + 1)

    d\left( I;\left( d_{2} ight) ight) = \sqrt{R^{2} - \frac{AB^{2}}{4}} = \sqrt{4 - \frac{12}{4}} = 1

    Do đó:

    \frac{\left| 3a - 4(a + 1) ight|}{\sqrt{3^{2} + ( - 4)^{2}}} = 1 \Leftrightarrow | - a - 4| = 5 \Leftrightarrow \left\lbrack \begin{matrix} a = 1 \\ a = - 9 \\ \end{matrix} ight.

    Với a = 1 \Rightarrow I(1;2) nên phương trình đường tròn là (x - 1)^{2} + (y - 2)^{2} = 4.

    Với a = - 9 \Rightarrow I( - 8; - 8) nên phương trình đường tròn là (x + 9)^{2} + (y + 8)^{2} = 4.

  • Câu 7: Nhận biết

    Trong các phương trình sau đây, phương trình nào là phương trình chính tắc của Elip?

    Phương trình Elip có dạng \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1;c^{2} = a^{2} - b^{2}

    Vậy phương trình cần tìm là \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1

  • Câu 8: Thông hiểu

    Trong hệ trục tọa độ Oxy, viết phương trình đường trung trực của đoạn thẳng MN biết M(1;0),N(3;6)?

    Đường thẳng trung trực của MN là đường thẳng đi qua trung điểm I(2;3) của MN và nhận \overrightarrow{MN} = (2;6) = 2(1;3) làm vectơ pháp tuyến. Khi đó:

    1(x - 2) + 3(y - 3) = 0

    \Leftrightarrow x + 3y - 11 = 0

    Vậy phương trình đường trung trực của MN là x + 3y - 11 = 0.

  • Câu 9: Thông hiểu

    Biết điểm M \in (H):\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1. Giả sử x_{M} = 8 thì khoảng cách từ điểm M đến các tiêu điểm của (H) bằng bao nhiêu?

    Ta có: M \in (H) và x_{M} = 8

    \Rightarrow \frac{8^{2}}{16} - \frac{{y_{M}}^{2}}{9} = 1 \Rightarrow y_{M} = \pm 3\sqrt{3}

    Có hai điểm M thỏa mãn là: M_{1}\left( 8;3\sqrt{3} ight),M_{2}\left( 8; - 3\sqrt{3} ight)

    Tiêu điểm của (H) là: F_{1}( - 5;0),F_{2}(0;5)

    \Rightarrow \left\{ \begin{matrix} M_{1}F_{1} = M_{2}F_{1} = 14 \\ M_{1}F_{2} = M_{2}F_{2} = 6 \\ \end{matrix} ight.

    Vậy đáp án cần tìm là: 6 và 14.

  • Câu 10: Thông hiểu

    Tính góc tạo bởi giữa hai đường thẳng d_{1}:6x - 5y + 15 = 0 và d_{2}:\left\{ \begin{matrix} x = 10 - 6t \\ y = 1 + 5t \\ \end{matrix} ight.\ .

    \left\{ \begin{matrix} d_{1}:6x - 5y + 15 = 0 ightarrow {\overrightarrow{n}}_{1} = (6; - 5) \\ d_{2}:\left\{ \begin{matrix} x = 10 - 6t \\ y = 1 + 5t \\ \end{matrix} ight.\ ightarrow {\overrightarrow{n}}_{2} = (5;6) \\ \end{matrix} ight.

    ightarrow {\overrightarrow{n}}_{1} \cdot {\overrightarrow{n}}_{2} = 0\overset{\varphi = \left( d_{1};d_{2} ight)}{ightarrow}\varphi = 90^{\circ}.

  • Câu 11: Thông hiểu

    Cho bất phương trình m{x^2} - (2m - 1)x + m + 1 < 0 (1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.

    Để m{x^2} - (2m - 1)x + m + 1 < 0 thì m{x^2} - (2m - 1)x + m + 1 \geqslant 0 nghiệm đúng với \forall x \in \mathbb{R}.

    Nghĩa là:\left\{ {\begin{array}{*{20}{c}} {a > 0} \\ {\Delta \leqslant 0} \end{array}} ight.

    \begin{matrix} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {{{\left( {2m - 1} ight)}^2} - 4m\left( {m + 1} ight) \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {4{m^2} - 4m + 1 - 4{m^2} - 4m \leqslant 0} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ { - 8m + 1 \leqslant 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m \geqslant \dfrac{1}{8}} \end{array}} ight. \Leftrightarrow m \geqslant \frac{1}{8} \hfill \\ \end{matrix}

  • Câu 12: Vận dụng

    Tìm hệ số của số hạng chứa x^{6} trong khai triển \left( 2x^{2} - \frac{3}{x} ight)^{n}(x eq 0), biết rằng \frac{2}{C_{n}^{2}} + \frac{14}{3C_{n}^{3}} = \frac{1}{n} \left( C_{n}^{k} ight. là số tổ hợp chập k của n phần tử).

    Xét phương trình \frac{2}{C_{n}^{2}} + \frac{14}{3C_{n}^{3}} = \frac{1}{n} (1)

    Điều kiện: n \geq 3,\ n\mathbb{\in N}

    (1) \Leftrightarrow \frac{2.(n - 2)!.2!}{n!} + \frac{14(n - 3)!.3!}{3.n!} = \frac{1}{n} \Leftrightarrow \frac{4}{n(n - 1)} + \frac{28}{n(n - 1)(n - 2)} = \frac{1}{n}

    \Leftrightarrow \frac{4}{n - 1} +\frac{28}{(n - 1)(n - 2)} = 1 \Leftrightarrow 4(n - 2) + 28 = (n - 1)(n- 2)

    \Leftrightarrow n^{2} - 7n - 18 = 0 \Leftrightarrow \left\lbrack\begin{matrix}n = 9 \ = - 2\ (l) \\\end{matrix} ight.

    Với n = 9 ta có: \left( 2x^{2} - \frac{3}{x} ight)^{9} = \sum_{k = 0}^{9}{C_{9}^{k}.}\left( 2x^{2} ight)^{9 - k}.\left( - \frac{3}{x} ight)^{k} = \sum_{k = 0}^{9}{C_{9}^{k}.}2^{9 - k}.( - 3)^{k}.x^{18 - 3k}

    Số hạng tổng quát của khai triển là C_{9}^{k}.2^{9 - k}.( - 3)^{k}.x^{18 - 3k}

    Cho 18 - 3k = 6 \Rightarrow k = 4 \Rightarrow hệ số của số hạng chứa x^{6} trong khai triển là C_{9}^{4}.2^{5}.( - 3)^{4} = 326592.

  • Câu 13: Vận dụng

    Cho đa giác đều có 24 đỉnh. Chọn ngẫu nhiên bốn đỉnh. Tính xác suất chọn ra được hình chữ nhật có các đỉnh là 4 trong 24 đỉnh của đa giác đó?

    Số phần tử của không gian mẫu là: n(\Omega) = C_{24}^{4}

    Ta vẽ đường tròn ngoại tiếp đa giác đều 24 đỉnh. Vẽ một đường kính của đường tròn này. Khi đó 2 nửa đường tròn đều chứa 12 đình.

    Với mỗi đỉnh thuộc nửa đường tròn thứ nhất ta đều có 1 đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại.

    Như vậy cứ 2 đỉnh thuộc đường tròn thứ nhất ta xác định được hai đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại, bốn đỉnh này tạo thành hình chữ nhật.

    Vậy số hình chữ nhật tạo thành từ 4 đa giác đã cho là C_{12}^{2}

    Xác suất cần tìm là: P = \frac{C_{12}^{2}}{C_{24}^{4}} = \frac{1}{161}.

  • Câu 14: Nhận biết

    Tìm phương trình chính tắc của parabol (P) biết (P) có tiêu điểm là F(0\ ;\ 5).

    Gọi phương trình chính tắc của (P) là: y^{2}= 2px.

    Do tọa độ tiêu điểm F(0\ ;\ 5) nên \frac{p}{2} = 5 \Leftrightarrow p =10.

    Vậy phương trình của (P) là: y^{2} = 20x.

  • Câu 15: Nhận biết

    Cho hai đường thẳng \left( d_{1} ight):2x + y + 15 = 0 và \left( d_{2} ight): - 4x - 2y + 3 = 0. Khẳng định nào sau đây đúng?

    Ta có: \frac{2}{- 4} = \frac{1}{- 2} eq \frac{15}{3} suy ra \left( d_{1} ight) và \left( d_{2} ight) song song với nhau.

  • Câu 16: Nhận biết

    Tổng tất cả các nghiệm của phương trình \sqrt{x^{2} + 3x - 2} = \sqrt{1 + x} bằng:

    \sqrt{x^{2} + 3x - 2} = \sqrt{1 + x} \Leftrightarrow \left\{ \begin{matrix} 1 + x \geq 0 \\ x^{2} + 3x - 2 = 1 + x \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ x^{2} + 2x - 3 = 0 \\ \end{matrix} ight.\ \Leftrightarrow x = 1.

    Phương trình chỉ có nghiệm x = 1 nên tổng các nghiệm bằng 1.

  • Câu 17: Thông hiểu

    Cho 40 tấm thẻ được đánh số theo thứ tự từ 1 đến 40. Chọn ngẫu nhiên 3 tấm thẻ. Tính xác suất để ba tấm thẻ được chọn có tổng các số ghi trên ba tấm thẻ đó là một số chẵn?

    Số phần tử không gian mẫu là: n(\Omega) = C_{40}^{3} = 9880

    Gọi A là biến cố chọn được 3 tấm thẻ có các số ghi trên ba tấm thẻ đó là một số chẵn.

    TH1: 2 số ghi số lẻ, 1 số ghi số chẵn ta có: C_{20}^{2}.C_{20}^{1} = 3800

    TH2: 3 số ghi số chẵn ta có: C_{20}^{3} = 1140

    Vậy xác suất để chọn được 3 tấm thẻ có tổng các số ghi trên các thẻ là một số chẵn là: \frac{3800 + 1140}{9880} = \frac{1}{2}

  • Câu 18: Nhận biết

    Giả sử một công việc phải hoàn thành qua 2 giai đoạn:

    Giai đoạn 1 có a cách thực hiện.

    Với mỗi cách thực hiện của giai đoạn 1 ta có b cách thực hiện cho giai đoạn 2.

    Khi đó số cách thực hiện công việc là:

    Áp dụng quy tắc nhân ta có số cách thực hiện công việc là a.b cách.

  • Câu 19: Thông hiểu

    Giáo viên chủ nhiệm mang đến lớp 6 cuốn sách khoa học và 4 cuốn sách tham khảo (các sách khác nhau từng đôi một). Giáo viên cho bạn C mượn ngẫu nhiên 3 quyển sách để đọc. Tính xác suất của biến cố: “X mượn ít nhất một cuốn sách tham khảo”.

    Số phần tử không gian mẫu là: n(\Omega) = C_{10}^{3} = 120

    Gọi A là biến cố: “X mượn ít nhất một cuốn sách tham khảo”.

    Khi đó \overline{A} là biến cố X mượn 3 cuốn sách khoa học. Khi đó: n\left( \overline{A} ight) = C_{6}^{3} = 20

    Vậy xác suất của biến cố A là: P(A) = 1 - P\left( \overline{A} ight) = 1 - \frac{20}{120} = \frac{5}{6}

  • Câu 20: Nhận biết

    Xét một phép thử có không gian mẫu \Omega gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố bất kì trong phép thử đó. Chọn phát biểu đúng dưới đây?

    Xét một phép thử có không gian mẫu \Omega gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố bất kì của phép thử đó. Khi đó A \subset \Omega là phát biểu đúng.

  • Câu 21: Thông hiểu

    Nguyên tố X có cấu hình electron là 1s22s22p3. Vậy vị trí X trong bảng tuần hoàn và công thức hợp chất khí với hydrogen của X là:

    Cấu hình electron: 1s22s22p3 

    ⇒ X có 7e ⇒ X ở ô số 7, chu kì 2, nhóm VA

    ⇒ hóa trị với H là 8 - 5 = 3

    ⇒ công thức hợp chất khí với hiđro là XH3

  • Câu 22: Thông hiểu

    Trong mặt phẳng Oxy có đường thẳng \Delta đi qua điểm A(1;1) và tạo với đường thẳng d:2x + 3y + 1 = 0 một góc bằng 45^{0}. Biết rằng \Delta có dạng ax - 5y + 4 = 0 và a'x + y - 6 = 0. Tính tổng hai giá trị a và a'?

    Gọi \overrightarrow{n} = (a;b) là vectơ pháp tuyến của đường thẳng \Delta.

    Phương trình tổng quát của đường thẳng \Delta là: ax + by - a - b = 0

    Ta có:

    \cos(d;\Delta) = \frac{|2a + 3b|}{\sqrt{13}.\sqrt{a^{2} + b^{2}}}

    \Leftrightarrow cos45^{0} = \frac{|2a + 3b|}{\sqrt{13}.\sqrt{a^{2} + b^{2}}}

    \Leftrightarrow \frac{\sqrt{2}}{2} = \frac{|2a + 3b|}{\sqrt{13}.\sqrt{a^{2} + b^{2}}}

    \Leftrightarrow \sqrt{2}.\sqrt{13}.\sqrt{a^{2} + b^{2}} = 2|2a + 3b|

    \Leftrightarrow 10a^{2} - 48ab - 10b^{2} = 0

    \Leftrightarrow \left\lbrack\begin{matrix}a = 5b \\a = - \dfrac{1}{5}b \\\end{matrix} ight.

    Vậy ta có phương trình của \Delta là: x - 5y + 4 = 0 và 5x + y - 6 = 0

    Vậy a = 1;a' = 5 \Rightarrow a + a' = 1 + 5 = 6

  • Câu 23: Nhận biết

    Trong mặt phẳng tọa độ Oxy, mỗi đường thẳng có bao nhiêu vectơ pháp tuyến?

    Một đường thẳng có vô số vectơ pháp tuyến và chúng có cùng phương với nhau.

  • Câu 24: Thông hiểu

    Xếp 6 chữ số 1, 1, 2, 2, 3, 4 thành hàng ngang sao cho hai chữ số giống nhau thì không xếp cạnh nhau. Hỏi có bao nhiêu cách sắp xếp như vậy?

    Số cách xếp sáu chữ số thành hàng một cách tùy ý là \frac{6!}{2!.2!} = 180.

    *) Tìm số cách xếp sáu chữ số sao cho có hai chữ số giống nhau đứng cạnh nhau

    +) TH1: Số cách xếp sao cho có hai chữ số 1 đứng cạnh nhau 5.\frac{4!}{2!} = 60.

    +) TH2: Số cách xếp sao cho có hai chữ số 2 đứng cạnh nhau 5.\frac{4!}{2!} = 60.

    +) TH3: Số cách xếp sao cho có hai chữ số 1 đứng cạnh nhau và hai chữ số 2 đứng cạnh nhau

    -) Nếu hai chữ số 1 ở vị trí (1;2)và (5;6) ta có số cách xếp là 2.3.2 = 12.

    -) Nếu hai chữ số 1 ở ba vị trí còn lại thì số các xếp là 3.2.2 =12.

    Vậy số cách xếp hai chữ số giống nhau đứng cạnh nhau là 60 + 60 - 12 - 12 = 96.

    \Rightarrow Số cách xếp không có hai chữ số giống nhau nào đứng cạnh nhau là 180 - 96 = 84.

  • Câu 25: Vận dụng

    Cho hai đường tròn (C):x^{2} + y^{2} = 1 và (C'):x^{2} + y^{2} - 2(m + 1)x + 4my - 5 = 0. Tìm giá trị tham số m để hai đường tròn tiếp xúc nhau?

    Dễ thấy đường tròn (C) có tâm O(0; 0) và bán kính R = 1

    Đường tròn (C’) có tâm I(m + 1; -2m) và bán kính R' = \sqrt{(m + 1)^{2} + 4m^{2} + 5}

    Ta thấy:

    OI = \sqrt{(m + 1)^{2} + 4m^{2}} < R' điểm O nằm trong đường tròn tâm I suy ra (C) và (C’) chỉ có thể tiếp xúc trong với nhau.

    Điều kiện để hai đường tròn tiếp xúc trong là:

    R' - R = OI

    \Leftrightarrow \sqrt{(m + 1)^{2} + 4m^{2} + 5} - 1 = \sqrt{(m + 1)^{2} + 4m^{2}}

    \Leftrightarrow \left\lbrack \begin{matrix} m = - 1 \\ m = \frac{3}{5} \\ \end{matrix} ight.

    Vậy có hai giá trị m thỏa mãn điều kiện là: m = - 1 hoặc m = \frac{3}{5}.

    VD

     

    1

  • Câu 26: Vận dụng cao

    Giả sử phương trình đường thẳng (\Delta):ax + by + c = 0 với a,b \in \mathbb{N}^{*} và \frac{b}{a} là phân số tối giản. Biết rằng đường thẳng (\Delta) đi qua điểm A(1;2) và cách điểm B( - 2;3) một khoảng bằng \frac{4\sqrt{2}}{\sqrt{5}}. Khi đó giá trị biểu thức Q = 3a + 2b + 1 là:

    Ta có:

    d\left( (\Delta);B ight) = \frac{4\sqrt{2}}{\sqrt{5}}

    \Leftrightarrow \frac{\left| a( - 2 - 1) + b(3 - 2) ight|}{\sqrt{a^{2} + b^{2}}} = \frac{8}{\sqrt{10}}

    \Leftrightarrow \sqrt{10}.| - 3a + b| = 8\sqrt{a^{2} + b^{2}}

    \Leftrightarrow 10\left( 9a^{2} - 6ab + b^{2} ight) = 64\left( a^{2} + b^{2} ight)

    \Leftrightarrow 13a^{2} - 30ab - 27b^{2} = 0(*)

    Với b = 0 thì (*) \Leftrightarrow 13a^{2} = 0 \Leftrightarrow a = 0 (loại do a^{2} + b^{2} > 0)

    Xét b eq 0 thì (*) \Leftrightarrow 13\left( \frac{a}{b} ight)^{2} - 30\left( \frac{a}{b} ight) - 27 = 0

    \Leftrightarrow \left\lbrack\begin{matrix}\dfrac{a}{b} = - \dfrac{9}{13}(ktm) \\\dfrac{a}{b} = 3(tm) \\\end{matrix} ight.

    Với \frac{a}{b} = 3 thì ta chọn a = 3;b = 1 \Rightarrow (\Delta):3x + y - 5 = 0

    Vậy Q = 3a + 2b + 1 = 12

  • Câu 27: Thông hiểu

    Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn \lbrack 40;60brack. Tính xác suất của biến cố: “Chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục”.

    Từ 40 đến 60 có 21 số nên n(\Omega) = 21

    Các số thỏa mãn yêu cầu đề bài là: 45;45;47;48;49;56;57;58;59

    Suy ra số kết quả thuận lợi cho biến cố: “Chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục” là 9.

    Suy ra xác suất của biến cố cần tìm là \frac{9}{21} = \frac{3}{7}

  • Câu 28: Vận dụng

    Cho tam thức bậc hai f(x) = ax^{2} + bx + c có đồ thị như hình vẽ dưới đây

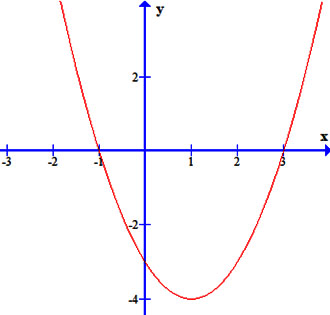
    Tìm bảng biến thiên của tam thức bậc hai

    Bảng biến thiên của tam thức bậc hai là

    Từ đồ thị ta có:

    Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ x = – 1 và x = 3

    => f(x) có 2 nghiệm phân biệt là x = –1; x = 3 ta loại các đáp án

    Tìm bảng biến thiên của tam thức bậc hai Tìm bảng biến thiên của tam thức bậc hai

    Ta lại có: f(x) nhận giá trị dương trên các khoảng (– ∞; –1) và (3; + ∞); f(x) nhận giá trị âm trên khoảng (–1; 3) ta loại đáp án 

    Tìm bảng biến thiên của tam thức bậc hai

    Vậy bảng biến thiên đúng là

    Tìm bảng biến thiên của tam thức bậc hai
  • Câu 29: Nhận biết

    Tính số chỉnh hợp chập 2 của 5 là:

    Số chỉnh hợp chập 2 của 5 là: A_{5}^{2}.

  • Câu 30: Thông hiểu

    Tính giá trị biểu thức S = 2^{5}C_{5}^{0} + 2^{4}C_{5}^{1} + 2^{3}C_{5}^{2} + 2.C_{5}^{4} + C_{5}^{5}

    Áp dụng công thức (a + b)^{n} cho a = 2,b = 1,n = 5 ta có:

    S = 2^{5}C_{5}^{0} + 2^{4}C_{5}^{1} + 2^{3}C_{5}^{2} + 2.C_{5}^{4} + C_{5}^{5}

    S = (2 + 1)^{5} = 243

  • Câu 31: Thông hiểu

    Phương trình tiếp tuyến của đường tròn (C):(x - 2)^{2} + (y + 3)^{2} = 5 tại điểm N( - 3;1) là:

    Đường tròn (C) có tâm I(2; - 3)

    Phương trình tiếp tuyến của (C) tại điểm N( - 3;1) là:

    (3 - 2)(x - 3) + ( - 1 + 3)(y + 1) = 0

    \Leftrightarrow x + 2y - 1 = 0

    Vậy phương trình tiếp tuyến của đường tròn tại N( - 3;1) là: x + 2y - 1 = 0

  • Câu 32: Vận dụng

    Viết phương trình tổng quát của đường thẳng (d). Biết rằng (d) đi qua điểm N(2;3) cắt đường thẳng (\Delta):3x - y + 1 = 0 tại điểm B có x_{B} > 0 sao cho BN = 2\sqrt{2}?

    Gọi B(b;3b + 1);(b > 0) là giao điểm của d và \Delta:3x - y + 1 = 0.

    Suy ra \overrightarrow{NB} = (b - 2;3b - 2)

    Theo giả thiết ta có:

    BN = 2\sqrt{2} \Leftrightarrow (b - 2)^{2} + (3b - 2)^{2} = 8

    \Leftrightarrow 10b^{2} - 16b = 0\Leftrightarrow \left\lbrack \begin{matrix}b = 0(ktm) \\b = \dfrac{8}{5}(tm) \\\end{matrix} ight.

    Khi đó \overrightarrow{NB} = \left( - \frac{2}{5};\frac{14}{5} ight) \Rightarrow \overrightarrow{n_{d}} = (7;1)

    Phương trình tổng quát của đường thẳng d là: 7(x - 2) + 1(y - 3) = 0 \Leftrightarrow 7x + y - 17 = 0

  • Câu 33: Vận dụng cao

    Tập tất cả các giá trị của tham số m để phương trình \sqrt{x^{2} - 2mx + 1} = m - 2 có nghiệm thực là

    * Với m < 2 ⇒ phương trình vô nghiệm

    * Với m ≥ 2, \sqrt{x^2-2mx+1}=m-2

    \Leftrightarrow x^2-2mx+1=m^2-4m+4

    \Leftrightarrow x^2-2mx-m^2+4m-3=0.

    Phương trình có nghiệm Δ′ = 2(m−1)2 + 1 > 0 đúng mọi m.

    Vậy m ≥ 2 là những giá trị cần tìm hay m thuộc [2;  + ∞).

  • Câu 34: Thông hiểu

    Tam thức bậc hai f(x)=−x^{2}+5x−6 nhận giá trị dương khi và chỉ khi

     Ta có: \Delta >0 và a=-1<0.

    Phươn trình f(x)=0 có hai nghiệm phân biệt x=2;x=3.

    Do đó f(x)>0 \Leftrightarrow x \in (2;3).

  • Câu 35: Thông hiểu

    Cặp bất phương trình nào sau đây là tương đương?

    Ta có: x-2 \le 0 \Leftrightarrow x \le2.

    Ta có: x^{2}(x-2)\leq 0 \Leftrightarrow x-2 \le0 (Vì x^2\ge0 với mọi giá trị x). Do đó x \le 2.

  • Câu 36: Thông hiểu

    Tập nghiệm của phương trình: \sqrt{3-x+x^{2}}-\sqrt{2+x-x^{2}}=1 là:

    Điều kiện: \left\{ {\begin{array}{*{20}{c}} {3 - x + {x^2} \geqslant 0} \\ {2 + x - {x^2} \geqslant 0} \end{array}} ight. => x \in \left[ { - 1,2} ight]

    Phương trình tương đương

    \begin{matrix} \sqrt {3 - x + {x^2}} - \sqrt {2 + x - {x^2}} = 1 \hfill \\ \Leftrightarrow \sqrt {3 - x + {x^2}} - 2 + 1 - \sqrt {2 + x - {x^2}} = 0 \hfill \\ \Leftrightarrow \dfrac{{{x^2} - x - 1}}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{{{x^2} - x - 1}}{{1 + \sqrt {2 + x - {x^2}} }} = 0 \hfill \\ \Leftrightarrow \left( {{x^2} - x - 1} ight)\left( {\dfrac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \dfrac{1}{{1 + \sqrt {2 + x - {x^2}} }}} ight) = 0 \hfill \\ \end{matrix}

    Ta có: \frac{1}{{\sqrt {3 - x + {x^2}} + 2}} + \frac{1}{{1 + \sqrt {2 + x - {x^2}} }} > 0,\forall x \in \left[ { - 1,2} ight]

    \begin{matrix} \Leftrightarrow {x^2} - x - 1 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{{1 - \sqrt 5 }}{2}} \\ {x = \dfrac{{1 + \sqrt 5 }}{2}} \end{array}} ight.\left( {tm} ight) \hfill \\ \end{matrix}

    Vậy tập nghiệm của phương trình là: \left\{ {\frac{{1 + \sqrt 5 }}{2};\frac{{1 - \sqrt 5 }}{2}} ight\}

  • Câu 37: Thông hiểu

    Cho Hypebol có độ dài trục thực và tiêu cự lần lượt là 14 và 20. Phương trình chính tắc của Hypebol là:

    Phương trình chính tắc của Hypebol có dạng \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1

    Ta có: \left\{ \begin{matrix} 2a = 14 \\ 2c = 20 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} a = 7 \\ c = 10 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} a^{2} = 49 \\ c^{2} = 100 \\ \end{matrix} ight.

    \Rightarrow b^{2} = c^{2} - a^{2} = 51

    Vậy phương trình chính tắc của Hypebol là: \frac{x^{2}}{49} - \frac{y^{2}}{51} = 1.

  • Câu 38: Nhận biết

    Cho tập A gồm 12 phần tử. Số tập con có 4 phần tử của tập A là:

    Theo định nghĩa tổ hợp. “ Giả sử tập A có n phần tử (n \geq 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho”.

    Do đó theo yêu cầu bài toán số tập con có 4 phần tử của tập A là C_{12}^{4}.

  • Câu 39: Nhận biết

    Số nghiệm của phương trình 3x + \sqrt{x - 8} = \sqrt{4 - x}. là bao nhiêu?

    Xét phương trình: 3x + \sqrt{x - 8} = \sqrt{4 - x}.

    Điều kiện: \left\{ \begin{matrix} x - 8 \geq 0 \\ 4 - x \geq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 8 \\ x \leq 4 \\ \end{matrix} ight.\ \Leftrightarrow x \in \varnothing..

    Vậy phương trình vô nghiệm.

  • Câu 40: Nhận biết

    Tam thức nào sau đây nhận giá trị không âm với mọi x ∈ ℝ?

    *x2 − x − 5 = 0 có 2 nghiệm phân biệt

    * − x2 − x − 1 = 0vô nghiệm, a =  − 1 < 0 nên  − x2 − x − 1 < 0, ∀x ∈ ℝ

    *2x2 + x = 0 có 2 nghiệm phân biệt

    *x2 + x + 1 = 0 vô nghiệm, a = 1 > 0 nên x2 + x + 1 > 0, ∀x ∈ ℝ thỏa ycbt.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 1 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 7 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 1
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập