Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 2

Mô tả thêm: Đề kiểm tra HK2 Toán 10 được biên soạn gồm 40 câu hỏi trắc nghiệm chia thành 4 mức độ bám sát chương trình sách Chân trời sáng tạo.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 0 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Vận dụng

    Số nghiệm của phương trình \sqrt{60 - 24x - 5x^{2}} = x^{2} + 5x - 10 là:

    ĐKXĐ: 60 − 24x − 5x2 ≥ 0

    Đặt t = \sqrt{60 - 24x - 5x^{2}}, (t≥0)pt trở thành \frac{1}{6}t^{2} + t - \frac{1}{6}x^{2} - x =0

    \Leftrightarrow t^{2} + 6t - x^{2} - 6x= 0 \Leftrightarrow \left\lbrack \begin{matrix}t = x \\t = - x - 6 \\\end{matrix} ight.

    \bullet \sqrt{60 - 24x - 5x^{2}} = x\Leftrightarrow \left\{ \begin{matrix}x \geq 0 \\x^{2} + 4x - 10 = 0 \\\end{matrix} ight.

    \Leftrightarrow x = - 2 +\sqrt{14}

    \bullet \sqrt{60 - 24x - 5x^{2}} = - x -6 \Leftrightarrow \left\{ \begin{matrix}- x - 6 \geq 0 \\x^{2} + 6x - 4 = 0 \\\end{matrix} ight.

    \Leftrightarrow x = - 3 -\sqrt{13}

    Vậy pt ban đầu có hai nghiệm x_{1} = - 2 -\sqrt{14},x_{2} = - 3 - \sqrt{13}.

  • Câu 2: Thông hiểu

    Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(–2\ ;\ 0),\ B(1\ ;\ 4) và đường thẳng d:\left\{ \begin{matrix} x = - t \\ y = 2 - t \\ \end{matrix} ight.. Tìm tọa độ giao điểm của đường thẳng AB và d.

    \left\{ \begin{matrix} A(–2\ ;\ 0),\ B(1\ ;\ 4) ightarrow AB:4x - 3y + 8 = 0 \\ d:\left\{ \begin{matrix} x = - t \\ y = 2 - t \\ \end{matrix} ight.\ ightarrow d:x - y + 2 = 0 \\ \end{matrix} ight.

    \overset{AB \cap d}{ightarrow}\left\{ \begin{matrix} 4x - 3y + 8 = 0 \\ x - y + 2 = 0 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} x = 2 \\ y = 0 \\ \end{matrix} ight.\ .

  • Câu 3: Nhận biết

    Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên?

    Thí nghiệm không phải là phép thử ngẫu nhiên là: “Quan sát vận động viên chạy bộ xem được bao nhiêu km/h”.

  • Câu 4: Thông hiểu

    Cho tọa độ hai điểm M\left( - 2\sqrt{3};\frac{3}{2} ight),N\left( 2;\frac{3\sqrt{3}}{2} ight). Viết phương trình chính tắc của elip có tâm là gốc tọa độ và đi qua hai điểm M;N?

    Gọi phương trình chính tắc của elip là: \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1;(a;b > 0)

    Do elip đi qua hai điểm M\left( - 2\sqrt{3};\frac{3}{2} ight),N\left( 2;\frac{3\sqrt{3}}{2} ight) nên ta có hệ phương trình:

    \left\{ \begin{matrix}\dfrac{12}{a^{2}} + \dfrac{9}{b^{2}} = 1 \\\dfrac{4}{a^{2}} + \dfrac{27}{b^{2}} = 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}a^{2} = 16 \\b^{2} = 9 \\\end{matrix} ight.

    Vậy phương trình chính tắc của elip thỏa mãn yêu cầu bài toán là: \frac{x^{2}}{16} + \frac{y^{2}}{9} = 1

  • Câu 5: Nhận biết

    Cho A là biến cố liên quan đến phép thử có không gian mẫu \Omega. Chọn khẳng định sai trong các khẳng định sau.

    Theo định nghĩa xác suất cổ điển, cho phép thử T có không gian mẫu \Omega. Giả thiết rằng các kết quả có thể của T là đồng khả năng, khi đó cho A là biến cố có liên quan đến phép thử có không gian mẫu \Omega. Thì xác suất của biến cố A được tính bởi công thức P(A) = \frac{n(A)}{n(\Omega)}, P(\varnothing) = 0, P(\Omega) = 1 , trong đó n(A);n(\Omega) tương ứng là số phần tử của biến cố A và của không gian mẫu.

    Vậy khẳng định sai là: P(\Omega) = 0.

  • Câu 7: Nhận biết

    Biết đường tròn (C) có tâm I(3; - 2) tiếp xúc với đường thẳng (d'):x - 5y + 1 = 0. Tính bán kính đường tròn (C)?

    Bán kính đường tròn là khoảng cách từ tâm I đến đường thẳng (d):

    Suy ra R = d\left( I,(d') ight) =\frac{\left| 3 - 5.( - 2) + 1 ight|}{\sqrt{1^{2} + ( - 5)^{2}}} =\frac{14}{\sqrt{26}}.

  • Câu 8: Thông hiểu

    Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):x^{2} + y^{2} - 2x + 4y - 20 = 0. Phương trình tiếp tuyến d của đường tròn (C) tại điểm M(5;1) là:

    Đường tròn (C) có tâm I(1; -2) và bán kính R = 5

    Điểm M \in (C) \Rightarrow \overrightarrow{IM} = (4;3)

    Vì d là tiếp tuyến của đường tròn (C) nên d nhận \overrightarrow{IM} là vecto pháp tuyến.

    Vậy d có phương trình 4(x - 5) + 3(y - 1) = 0 hay 4x + 3y - 23 = 0.

  • Câu 9: Thông hiểu

    Từ tập hợp các chữ số A = \left\{ 1,2,3,4,5,6 ight\} có thể lập được bao nhiêu số lẻ có bốn chữ số khác nhau?

    Gọi số tự nhiên có bốn chữ số cần tìm có dạng \overline{abcd};(a eq 0)

    Ta có: \overline{abcd} là số lẻ nên d là số lẻ. => Số cách chọn d có 3 cách.

    Tiếp theo chọn a có 5 cách chọn

    Sau đó chọn b có 4 cách chọn

    Cuối cùng chọn c có 3 cách chọn

    Vậy có thể lập được 3.5.4.3 = 180(số) thỏa mãn yêu cầu đề bài.

  • Câu 10: Nhận biết

    Tìm số tự nhiên n thỏa A_{n}^{2}=210

     Điều kiện: n \ge 2.

    Ta có: A_n^2 = 210 \Leftrightarrow \frac{{n!}}{{(n - 2)!}} = 210\Leftrightarrow n(n - 1) = 210 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{n = 15}\\{n = - 14}\end{array}} ight.

    Vậy n=15.

  • Câu 11: Thông hiểu

    Một lớp có 43 học sinh trong đó có 23 học sinh nữ và 20 học sinh nam. Chọn ngẫu nhiên 5 học sinh. Xác suất để 5 học sinh được chọn có cả nam và nữ gần nhất với kết quả nào dưới đây?

    Số phần tử của không gian mẫu là: n(\Omega) = C_{43}^{5} = 962598

    Số cách chọn 5 học sinh chỉ có nam hoặc chỉ có nữ là:

    C_{20}^{5} + C_{23}^{5} = 49153

    Số cách chọn 5 học sinh có cả nam và nữ là: C_{20}^{5}

    962598 - 49153 = 913445

    Xác suất của biến cố 5 học sinh được chọn có cả nam và nữ là: P = \frac{913445}{962598} \approx 0,95

  • Câu 12: Thông hiểu

    Có bốn hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có người?

    Vì mỗi hành khách có 4 cách chọn toa tàu nên: n(\Omega) = 4^{4} = 256

    Để xếp theo yêu cầu của bài toán ta thực hiện các bước liên tiếp như sau:

    Chọn 1 toa để xếp 3 người ta có: C_{4}^{1} = 4

    Chọn 3 người để xếp vào toa đó là: C_{4}^{3} = 4

    Chọn 1 toa từ 3 toa còn lại để xếp người còn lại vào: C_{3}^{1} = 3

    Theo quy tắc nhân ta có: 4.4.3 = 48

    Vậy xác suất cần tìm là: \frac{48}{256} = \frac{3}{16}

  • Câu 13: Nhận biết

    Tìm hệ số của số hạng chứa x^{31} trong khai triển \left( x + \frac{1}{x^{2}} ight)^{40}.

    Ta có: \left( x + \frac{1}{x^{2}} ight)^{40} = \sum_{k = 0}^{40}{C_{40}^{k}.x^{40 - k}}.\left( \frac{1}{x^{2}} ight)^{k} = \sum_{k = 0}^{40}{C_{40}^{k}.x^{40 - 3k}}.

    Số hạng tổng quát của khai triển là: T_{k + 1} = C_{40}^{k}.x^{40 - 3k}.

    Số hạng chứa x^{31} trong khai triển tương ứng với 40 - 3k = 31 \Leftrightarrow k = 3.

    Vậy hệ số cần tìm là: C_{40}^{3} = C_{40}^{37} (theo tính chất của tổ hợp: C_{n}^{k} = C_{n}^{n - k}).

  • Câu 14: Nhận biết

    Cho Parabol (P) có phương trình y^{2} = 4x. Tìm đường chuẩn của (P).

    Từ phương trình của (P), ta có: 2p = 4 nên p = 2.

    Suy ra (P) có tiêu điểm là F(1\ ;\ 0) và đường chuẩn là x + 1 = 0.

  • Câu 15: Nhận biết

    Trong hệ trục tọa độ \left( O;\overrightarrow{i};\overrightarrow{j} ight), tọa độ của vectơ \overrightarrow{a} = 2\overrightarrow{i} + 3\overrightarrow{j} là:

    Tọa độ vectơ \overrightarrow{a} = (2;3).

  • Câu 16: Thông hiểu

    Có bao nhiêu cách xếp 5 bạn A, B, C, D, E vào một băng ghế dài sao cho C luôn ở chính giữa.

    Giả sử 5 bạn ngồi vào 5 vị trí được đánh số 1, 2, 3, 4, 5.

    Xếp bạn C vào vị trí số 3: có 1 cách.

    Xếp 1 bạn trong 4 bạn còn lại vào vị trí 1: có 4 cách.

    Xếp 1 bạn trong 3 bạn còn lại vào vị trí 2: có 3 cách.

    Xếp 1 bạn trong 2 bạn còn lại vào vị trí 3: có 2 cách.

    Xếp bạn còn lại vào vị trí 5: có 1 cách.

    Áp dụng quy tắc nhân, có 1.4.3.2 = 24 cách xếp 5 bạn vào ghế băng dài sao cho C luôn ở chính giữa.

  • Câu 17: Thông hiểu

    Đường Hyperbol \frac{x^{2}}{20} - \frac{y^{2}}{16} = 1 có tiêu cự bằng:

    Ta có : \left\{ \begin{matrix} a^{2} = 20 \\ b^{2} = 16 \\ c^{2} = a^{2} + b^{2} \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} a = 2\sqrt{5} \\ b = 4 \\ c = 6 \\ \end{matrix} ight.. Tiêu cự 2c = 12.

  • Câu 18: Nhận biết

    Cho phương trình ax + by + c = 0\ \ \ (*) với a^{2} + b^{2} > 0. Mệnh đề nào sau đây là mệnh đề sai?

    Mệnh đề sai là: “Điểm M\left( x_{0};y_{0} ight) thuộc đường thẳng (*) khi và chỉ khi ax_{0} + by_{0} + c eq 0.”

  • Câu 19: Vận dụng

    Cho hai đường thẳng \left( d_{1} ight):x + my + 2m - 1 = 0 và \left( d_{2} ight):\left\{ \begin{matrix} x = m + 2y \\ y = - 5 + t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight) với m là tham số. Tìm giá trị của tham số m để hai đường thẳng tạo với nhau một góc bằng nửa góc vuông?

    VTPT của hai đường thẳng \left( d_{1} ight);\left( d_{2} ight) lần lượt là \overrightarrow{n_{1}} = (1;m);\overrightarrow{n_{2}} = (1; - 2)

    Để hai đường thẳng tạo với nhau một góc bằng 45^{0} thì

    \cos\left( \left( d_{1} ight);\left( d_{2} ight) ight) = cos45^{0} = \frac{\sqrt{2}}{2}

    \Leftrightarrow \cos\left( \overrightarrow{n_{1}};\overrightarrow{n_{2}} ight) = \frac{\sqrt{2}}{2} \Leftrightarrow \frac{\left| 1.1 + m.( - 2) ight|}{\sqrt{m^{2} + 1}.\sqrt{1^{2} + ( - 2)^{2}}} = \frac{\sqrt{2}}{2}

    \Leftrightarrow \frac{|2m - 1|}{\sqrt{m^{2} + 1}.\sqrt{5}} = \frac{\sqrt{2}}{2} \Leftrightarrow \frac{(2m - 1)^{2}}{5\left( m^{2} + 1 ight)} = \frac{1}{2}

    \Leftrightarrow 2(2m - 1)^{2} = 5\left( m^{2} + 1 ight) \Leftrightarrow 3m^{2} - 8m - 3 = 0

    \Leftrightarrow \left\lbrack\begin{matrix}m = 3 \\m = - \dfrac{1}{3} \\\end{matrix} ight.

    Vậy \left\lbrack \begin{matrix}m = 3 \\m = - \dfrac{1}{3} \\\end{matrix} ight..

  • Câu 20: Thông hiểu

    Phương trình\frac{x^{2}-4x-2}{\sqrt{x-2}}=\sqrt{x-2} có tất cả bao nhiêu nghiệm?

     Điều kiện: x>2.

    Ta có: \frac{x^{2}-4x-2}{\sqrt{x-2}}=\sqrt{x-2} \Rightarrow x^2-4x-2=x-2x^2-5x=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 5}\end{array}} ight..

    Loại x=0. Do đó phương trình có 1 nghiệm.

  • Câu 21: Thông hiểu

    Số giá trị nguyên của x để tam thức f(x)=2x^{2}−7x−9 nhận giá trị âm là:

     Ta có: \Delta >0 và a=2>0.

    Phương trình f(x)=0 có hai nghiệm x=-1;x=\frac92.

    Do đó f(x)<0 \Leftrightarrow -1 < x < \frac92 \Leftrightarrow x=\{0;1;2;3;4\} (5 giá trị).

  • Câu 22: Thông hiểu

    Khoảng cách nhỏ nhất từ điểm M(15;1) đến một điểm bất kì thuộc đường thẳng \Delta:\left\{ \begin{matrix} x = 2 + 3t \\ y = t \\ \end{matrix} ight. bằng:

    \Delta:\left\{ \begin{matrix} x = 2 + 3t \\ y = t \\ \end{matrix} ight.\ ightarrow \Delta:x - 3y - 2 = 0

    \overset{\forall N \in \Delta}{ightarrow}MN_{\min} = d(M;\Delta) = \frac{|15 - 3 - 2|}{\sqrt{1 + 9}} = \sqrt{10}.

  • Câu 23: Nhận biết

    Cho tam thức bậc hai f(x) = {x^2} - 10x + 2. Kết luận nào sau đây đúng?

    Ta có:

    \begin{matrix}f\left( { - 2} ight) = {\left( { - 2} ight)^2} - 10.\left( { - 2} ight) + 2 = 26 > 0 \hfill \\ f\left( 1 ight) = {\left( 1 ight)^2} - 10.\left( 1 ight) + 2 = - 7 < 0 \hfill \\ \end{matrix}

    Vậy khẳng định đúng là f(–2) > 0.

  • Câu 24: Thông hiểu

    Phương trình x2 + 2(m+2)x − 2m − 1 = 0 (m là tham số) có nghiệm khi

    Xét phương trình x2 + 2(m+2)x − 2m − 1 = 0, có Δ′x = (m+2)2 + 2m + 1.

    Yêu cầu bài toán ⇔  Δ′x ≥ 0 ⇔ m2 + 4m + 4 + 2m + 1 ≥ 0 ⇔ m2 + 6m + 5 ≥ 0

    \Leftrightarrow (m + 1)(m + 5) \geq 0 \Leftrightarrow \left\lbrack \begin{matrix} m \geq - \ 1 \\ m \leq - \ 5 \\ \end{matrix} ight. là giá trị cần tìm.

  • Câu 25: Nhận biết

    Cho hình elip có độ dài trục lớn và độ dài trục nhỏ lần lượt bằng 6 và 0. Viết phương trình elip.

    Ta có: \left\{ \begin{matrix} 2a = 6 \Rightarrow a = 3 \\ 2b = 4 \Rightarrow b = 2 \\ \end{matrix} ight.

    Phương trình elip là: \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1

  • Câu 26: Vận dụng cao

    Cho một đa giác đều (H) có 20 đỉnh. Chọn ngẫu nhiên ba đỉnh của (H). Tính xác suất để ba đỉnh được chọn tạo thành một tam giác vuông cân?

    Số phần tử của không gian mẫu C_{20}^{3} = 1140

    Gọi A là biến cố: “Chọn được ba đỉnh tạo thành một tam giác vuông cân”.

    Ba đỉnh được chọn tạo thành một tam giác vuông cân khi và chỉ khi trong ba đỉnh được chọn có hai đỉnh là đầu mút của một đường kính của đường tròn ngoại tiếp (H) và đỉnh còn lại là giao điểm (hai giao điểm) giữa đường thẳng qua tâm vuông góc với đường kính đã chọn và đường tròn ngoại tiếp (H).

    Đa giác đều có 20 đỉnh nên có: 20:2 = 10 đường kính.

    Số cách chọn 1 đường kính là 10

    Số cách chọn 1 đỉnh còn lại là 2

    Suy ra số tam giác vuông cân có thể tạo thành là 10.2 = 20 tam giác

    Suy ra xác suất của biến cố: “ba đỉnh được chọn tạo thành một tam giác vuông cân” là: \frac{20}{1140} = \frac{1}{57}

  • Câu 27: Nhận biết

    Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?

    Loại đáp án 5x^{2} + 4y^{2} + x - 4y + 1 = 0. vì không có dạng x^{2} + y^{2} - 2ax - 2by + c = 0.

    Xét đáp án

    x^{2} + y^{2} + 2x - 4y + 9 = \ 0 ightarrow a = - 1,\ b = 2,\ c = - 9 ightarrow a^{2} + b^{2} - c < 0 ightarrowloại.

    Xét đáp án

    x^{2} + y^{2} - 6x + 4y + 13 = 0 ightarrow a = 3,\ b = - 2,\ c = 13 ightarrow a^{2} + b^{2} - c < 0 ightarrowloại.

    Xét đáp án

    2x^{2} + 2y^{2} - 8x - 4y - 6 = 0 \Leftrightarrow x^{2} + y^{2} - 4x - 2y - 3 = 0 ightarrow \left\{ \begin{matrix} a = 2 \\ b = 1 \\ c = - 3 \\ \end{matrix} ight.\ ightarrow a^{2} + b^{2} - c > 0.

    Chọn đáp án này.

  • Câu 28: Nhận biết

    Đường thẳng nào sau đây vuông góc với đường thẳng 4x - 3y + 1 = 0 ?

    Kí hiệu d:4x - 3y + 1 = 0 ightarrow {\overrightarrow{n}}_{d} = (4; - 3).

    (i) Xét đáp án d_{1}:\left\{ \begin{matrix} x = 4t \\ y = - 3 - 3t \\ \end{matrix} ight.\ ightarrow {\overrightarrow{n}}_{1} = (3;4) ightarrow {\overrightarrow{n}}_{1} \cdot {\overrightarrow{n}}_{d} = 0 nên chọn đáp án này.

    (ii) Tương tự kiểm tra và loại các đáp án còn lại.

  • Câu 29: Thông hiểu

    Trong hệ trục tọa độ Oxy cho đường thẳng (d):2x - y - 4 = 0. Một đường tròn (C) tiếp xúc với các trục tọa độ và có tâm nằm trên đường thẳng (d). Kết quả nào dưới đây đúng?

    Ta có tâm đường tròn thuộc đường thẳng d nên I(m;2m - 4) \in (d). Theo giả thiết để bài ta có:

    d(I;Ox) = d(I;Oy)

    \Leftrightarrow |2m - 4| = |m| \Leftrightarrow \left\lbrack \begin{matrix} m = 4 \\ m = \frac{4}{3} \\ \end{matrix} ight.

    Với m = \frac{4}{3} \Rightarrow I\left( \frac{4}{3}; - \frac{4}{3} ight)

    \Rightarrow R = d(I;Oy) = |m| = \frac{4}{3}

    Vậy phương trình đường tròn là: \left( x - \frac{4}{3} ight)^{2} + \left( x + \frac{4}{3} ight)^{2} = \frac{16}{9}

    Với m = 4 \Rightarrow I(4;4)

    \Rightarrow R = d(I;Oy) = |m| = 4

    Vậy phương trình đường tròn là: (x - 4)^{2} + (y + 4)^{2} = 16.

  • Câu 30: Nhận biết

    Có 6 học sinh và 2 thầy giáo được xếp thành hàng ngang. Đếm số cách xếp sao cho hai thầy giáo không đứng cạnh nhau?

    Xếp 8 người thành hàng ngang có P_{8} cách.

    Xếp 8 người thành hàng ngang sao cho 2 thầy giáo đứng cạnh nhau có 7.2!.6! cách.

    Vậy số cách xếp cần tìm là. P_{8} - 7.2!.6! = 30240 cách.

  • Câu 31: Nhận biết

    Gọi S là tập nghiệm của bất phương trình {x^2} - 8x + 7 \geqslant 0. Trong các tập hợp sau, tập nào không là tập con của S?

    Tam thức bậc hai f\left( x ight) = {x^2} - 8x + 7 có hai nghiệm phân biệt là: {x_1} = 1;{x_2} = 7

    Vì a = 1 > 0 nên f\left( x ight) \geqslant 0 khi x \in \left( { - \infty ;1} ight] \cup \left[ {7; + \infty } ight).

    Tập không phải tập con của S là: [6; + ∞)

  • Câu 32: Thông hiểu

    Biết n là số nguyên dương thỏa mãn C_{n}^{n - 1} + C_{n}^{n - 2} = 78, số hạng chứa x^{8} trong khai triển \left( x^{3} - \frac{2}{x} ight)^{n} là:

    Ta có: C_{n}^{n - 1} + C_{n}^{n - 2} = 78 \Leftrightarrow \frac{n!}{(n - 1)!.1!} + \frac{n!}{(n - 2)!.2!} = 78 \Leftrightarrow n + \frac{(n - 1)n}{2} = 78

    \Leftrightarrow n^{2} + n - 156 = 0 \Leftrightarrow \left\lbrack \begin{matrix} n = 12 \\ n = - 13 \\ \end{matrix} ight.\ \Leftrightarrow n = 12 (vì n là số nguyên dương).

    Số hạng tổng quát trong khai triển \left( x^{3} - \frac{2}{x} ight)^{12}là: ( - 1)^{k}C_{12}^{k}\left( x^{3} ight)^{12 - k}\left( \frac{2}{x} ight)^{k} = ( - 1)^{k}C_{12}^{k}.2^{k}.x^{36 - 4k}.

    Cho 36 - 4k = 8 \Leftrightarrow k = 7.

    Vậy số hạng chứa x^{8} trong khai triển \left( x^{3} - \frac{2}{x} ight)^{12} là - C_{12}^{7}.2^{7}.x^{8} = - 101376x^{8}.

  • Câu 33: Vận dụng

    Cho khai triển (1 + 3x)^{n} = a_{0} + a_{1}x^{1} + ... + a_{n}x^{n} trong đó n\mathbb{\in N}* và các hệ số thỏa mãn hệ thức a_{0} + \frac{a_{1}}{3} + ... + \frac{a_{n}}{3^{n}} = 4096. Hệ số lớn nhất là:

    Xét khai triển (1 + 3x)^{n} = a_{0} + a_{1}x^{1} + ... + a_{n}x^{n}.

    Cho x = \frac{1}{3} ta được \left( 1 + 3.\frac{1}{3} ight)^{n} = a_{0} + \frac{a_{1}}{3^{1}} + ... + \frac{a_{n}}{3^{n}} \Rightarrow 2^{n} = 4096 \Leftrightarrow n = 12.

    Khi đó (1 + 3x)^{12} = \sum_{k = 0}^{12}{C_{12}^{k}.3^{k}.x^{k}}.

    Ta có hệ số a_{k} = 3^{k}C_{12}^{k} = 3^{k}.\frac{12!}{k!.(12 - k)!}

    Hệ số a_{k} lớn nhất nên \left\{ \begin{matrix} a_{k} \geq a_{k - 1} \\ a_{k} \geq a_{k + 1} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 3^{k}.\frac{12!}{k!.(12 - k)!} \geq 3^{k - 1}.\frac{12!}{(k - 1)!.(12 - k + 1)!} \\ 3^{k}.\frac{12!}{k!.(12 - k)!} \geq 3^{k + 1}.\frac{12!}{(k + 1)!.(12 - k - 1)!} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} \frac{3}{k} \geq \frac{1}{13 - k} \\ \frac{1}{12 - k} \geq \frac{3}{k + 1} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 39 - 3k \geq k \\ k + 1 \geq 36 - 3k \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} k \leq \frac{39}{4} \\ k \geq \frac{35}{4} \\ \end{matrix} ight.

    Vì k\mathbb{\in N} nên nhận k = 9.

    Vậy hệ số lớn nhất a_{9} = 3^{9}.C_{12}^{9} = 4330260..

  • Câu 34: Nhận biết

    Có bao nhiêu số hạng trong khai triển (6x + 4)^{4}?

    Trong khai triển nhị thức (6x + 4)^{4} có n = 4 nên có 5 số hạng.

  • Câu 35: Vận dụng cao

    Trên màn hình ra-đa của đài kiểm soát không lưu sân bay A có hệ trục tọa độ Oxy (như hình vẽ) trong đó đơn vị trên mỗi trục tính theo ki – lô – mét và đài kiểm soát được coi là gốc tọa độ O(0;0).

    Nếu máy bay trong phạm vi cách đài kiểm soát 500km thì sẽ hiển thị trên màn hình ra-đa. Một máy bay khởi hành từ sân bay X lúc 10 giờ. Sau thời gian t (giờ) vị trí của máy bay được xác định bởi điểm M có tọa độ như sau: \left\{ \begin{matrix}x = \dfrac{1600}{3} - \dfrac{1400}{3}.t \\y = \dfrac{1900}{3} - \dfrac{1400}{3}.t \\\end{matrix} ight.. Lúc mấy giờ thì máy bay bay gần đài kiểm soát không lưu nhất?

    Gọi M là vị trí máy báy

    Ta có:

    OM = \sqrt{x^{2} + y^{2}}

    = \sqrt{\left( \frac{1600}{3} - \frac{1400}{3}t ight)^{2} + \left( \frac{1900}{3} - \frac{1400}{3}.t ight)^{2}}

    = \sqrt{\left( \frac{1600}{3} - \frac{1400}{3}t ight)^{2} + \left( \frac{1400}{3}.t - \frac{1900}{3} ight)^{2}}

    Áp dụng bất đẳng thức Bunhiacopski ta có:

    \left( 1^{2} + 1^{2} ight)\left( a^{2} + b^{2} ight) \geq (a + b)^{2}

    \Leftrightarrow a^{2} + b^{2} \geq \frac{1}{2}(a + b)^{2}

    Dấu bằng xảy ra khi và chỉ khi

    a = b \Leftrightarrow \frac{1600}{3} - \frac{1400}{3}t = \frac{1400}{3}.t - \frac{1900}{3}

    \Leftrightarrow t = 1,25(h)

    Khi đó:

    OM = \sqrt{\left( \frac{1600}{3} - \frac{1400}{3}t ight)^{2} + \left( \frac{1400}{3}.t - \frac{1900}{3} ight)^{2}}

    \geq \sqrt{\frac{1}{2}\left( \frac{1600}{3} - \frac{1400}{3}t + \frac{1400}{3}.t - \frac{1900}{3} ight)^{2}}

    = \sqrt{\frac{1}{2}\left( \frac{1600}{3} - \frac{1900}{3} ight)^{2}} = 50\sqrt{2}(km)

  • Câu 36: Thông hiểu

    Phương trình nào sau đây là phương trình tổng quát của đường thẳng d:\left\{ \begin{matrix} x = 3 - 5t \\ y = 1 + 4t \\ \end{matrix} ight.?

    Ta có: d:\left\{ \begin{matrix} x = 3 - 5t \\ y = 1 + 4t \\ \end{matrix} ight.\ ightarrow \left\{ \begin{matrix} A(3;1) \in d \\ {\overrightarrow{u}}_{d} = ( - 5;4) ightarrow {\overrightarrow{n}}_{d} = (4;5) \\ \end{matrix} ight.\ \overset{ightarrow}{}d:4(x - 3) + 5(y - 1) = 0

    \Leftrightarrow d:4x + 5y - 17 = 0.

  • Câu 37: Vận dụng

    Có bao nhiêu giá trị nguyên dương của x thỏa mãn \frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} < \frac{2x}{2x - x^{2}} ?

    Điều kiện: \left\{ \begin{matrix} x^{2} - 4 eq 0 \\ x + 2 eq 0 \\ 2x - x^{2} eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x eq 0 \\ x eq \pm \ 2 \\ \end{matrix} ight.\ . Bất phương trình:

    \frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} < \frac{2x}{2x - x^{2}} \Leftrightarrow \frac{x + 3}{x^{2} - 4} - \frac{1}{x + 2} + \frac{2x}{x^{2} - 2x} < 0 \Leftrightarrow \frac{2x + 9}{x^{2} - 4} < 0.

    Bảng xét dấu:

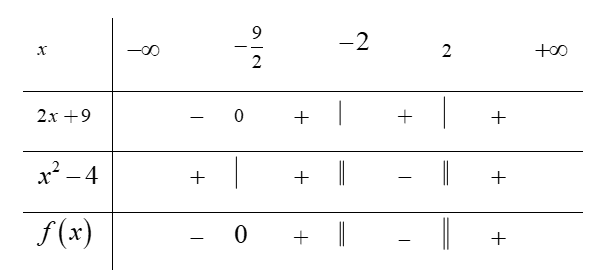
    Dựa vào bảng xét dấu, ta thấy \frac{2x + 9}{x^{2} - 4} < 0 \Leftrightarrow x \in \left( - \ \infty; - \frac{9}{2} ight) \cup ( - \ 2;2).

    Vậy có chỉ có duy nhất một giá trị nguyên dương của x (x=1) thỏa mãn yêu cầu.

  • Câu 38: Thông hiểu

    Một đội cổ động viên gồm có 3 người mặc áo vàng, 4 người mặc áo đỏ, 5 người mặc áo xanh. Hỏi có bao nhiêu cách chọn 2 người sao cho luôn có 2 màu áo khác nhau.

     Trường hợp 1: 1 áo vàng + 1 áo đỏ

    Có: C_3^1.C_4^1 = 12 (cách).

    Trường hợp 2: 1 áo đỏ + 1 áo xanh

    Có: C_4^1.C_5^1 = 20 (cách).

    Trường hợp 3: 1 áo xanh + 1 áo vàng

    Có: C_5^1.C_3^1 = 15 (cách)

    Vậy có 12+20+15=47 (cách).

  • Câu 39: Nhận biết

    Tìm tập nghiệm của phương trình \sqrt{4x+1}+5=0

     Nhận xét: \sqrt{4x+1} \ge 0 \Leftrightarrow \sqrt{4x+1}+5 >0. 

    Do đó \sqrt{4x+1}+5=0 vô lí. 

    Vậy S=\varnothing.

  • Câu 40: Thông hiểu

    Tập nghiệm S của bất phương trình 5(x+1)−x(7−x)>−2x là:

     Ta có: 5(x+1)−x(7−x)>−2x \Leftrightarrow x^2+5>0 (hiển nhiên).

    Vậy S = \mathbb{R}.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 5 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 2 Toán 10 Chân trời sáng tạo – Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập