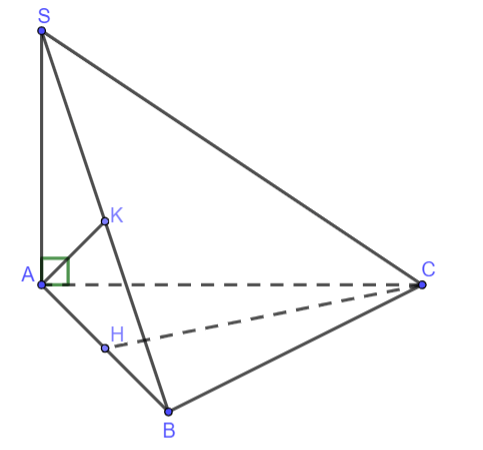
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy, I là trung điểm của AC, H là hình chiếu của I trên SC. Kí hiệu d(a, b) là khoảng cách giữa hai đường thẳng a và b. Khẳng định nào sau đây là đúng?
Hình vẽ minh họa:
Ta có:
=> d(SA, BC) = AB








 . Tính đạo hàm của hàm số tại
. Tính đạo hàm của hàm số tại