Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA ⊥ (ABCD) , ![]() . Góc giữa SC với mặt phẳng (ABCD) là:
. Góc giữa SC với mặt phẳng (ABCD) là:
Hình vẽ minh họa:
Ta có:
Lại có:
=>
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA ⊥ (ABCD) , ![]() . Góc giữa SC với mặt phẳng (ABCD) là:
. Góc giữa SC với mặt phẳng (ABCD) là:
Hình vẽ minh họa:
Ta có:
Lại có:
=>
Tính giá trị biểu thức: ![]() . Biết hàm số
. Biết hàm số ![]() xác định bởi công thức
xác định bởi công thức ![]() .
.
Kết quả: ![]() 2017/2018
2017/2018
(Kết quả ghi dưới dạng phân số tối giản dạng a/b)
Tính giá trị biểu thức: . Biết hàm số
xác định bởi công thức
.
Kết quả: 2017/2018
(Kết quả ghi dưới dạng phân số tối giản dạng a/b)
Ta có:
Khi đó:
Đạo hàm của hàm số ![]() là:
là:
Ta có:
Kết quả khi thu gọn biểu thức ![]() khi
khi ![]() là:
là:
Ta có:
Sơ đồ phân phối điện như hình vẽ:

Điện được tải từ trạm điện P đến nơi tiêu thụ Q qua các trạm tải nhỏ A, B, C. Xác suất có sự cố kĩ thuật sau một thời gian hoạt động của các trạm tải nhỏ A, B, C lần lượt là ![]() . Hãy tính xác suất để nơi tiêu thụ Q không bị mất điện (biết rằng các trạm tải nhỏ hoạt động độc lập với nhau).
. Hãy tính xác suất để nơi tiêu thụ Q không bị mất điện (biết rằng các trạm tải nhỏ hoạt động độc lập với nhau).
Gọi Q là biến cố nơi tiêu thụ Q không mất điện
A, B, C là biến cố các trạm tải nhỏ A, B, C gặp sự cố kĩ thuật.
Ta có:
Suy ra
Cho hình chóp ![]() có đáy là hình vuông cạnh bằng
có đáy là hình vuông cạnh bằng ![]() . Biết góc giữa hai mặt phẳng
. Biết góc giữa hai mặt phẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng
bằng ![]() ,
, ![]() . Tính tan góc giữa
. Tính tan góc giữa ![]() và mặt phẳng
và mặt phẳng ![]() , biết thể tích khối chóp
, biết thể tích khối chóp ![]() bằng
bằng ![]() ?
?
Hình vẽ minh họa
Kẻ , gọi
Ta có:
Lại có:
Do tam giác SAB cân tại S nên H là trung điểm của AB
Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
Chọn vị trí cho hai nhóm 3 nam và 3 nữ có 2 cách chọn (1 nhóm ở vị trí chẵn và nhóm còn lại ở vị trí lẻ)
Xếp 3 nam có: 3.2.1 = 6 cách xếp
Xếp 3 nữ có: 3.2.1 = 6 cách xếp
Vậy có 2.(3.2.1)2 = 72 cách xếp
Gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Gọi biến cố lần đầu xuất hiện mặt 3 chấm là A và biến cố lần thứ hai xuất hiện mặt 3 chấm là B. Khẳng định nào dưới dây sai?
Hai biến cố A và B có thể cùng xảy ra suy ra khẳng định sai là: “ là hai biến cố xung khắc.”
Tính thể tích khối lập phương có cạnh bằng ![]() ?
?
Ta có:
Trong các phát biểu sau, phát biểu nào sau là đúng?
Đáp án đúng là "Nếu hàm số có đạo hàm tại
thì nó liên tục tại điểm đó."
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60◦. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
Hình vẽ minh họa:
Gọi H là hình chiếu của S lên (ABCD).
Ta có:
=> AB ⊥ MH
=> MH là đường trung bình của hình vuông ABCD
Giả sử MH cắt CD tại N, ta có N là trung điểm CD
Ta cũng có SN ⊥ CD nên
Gọi P là trung điểm BC, ta có MP // AC nên AC // (SMP)
Do đó, d(SM, AC) = d(AC,(SMP)) = d(O,(SMP))
Gọi K là hình chiếu của H lên MP (nhận thấy HK // OB), I là hình chiếu của H lên SK
Khi đó d(H, (SMP)) = HI
Áp dụng định lý cosin cho tam giác SMN, ta có:
Xét tam giác vuông SHN ta có:
Xét tam giác SHK vuông tại H, ta có:
Mặt khác:
Biết hai biến cố ![]() độc lập với nhau và
độc lập với nhau và ![]() . Tính giá trị
. Tính giá trị ![]() ?
?
Do A và B là hai biến cố độc lập với nhau nên
Đạo hàm cấp hai của hàm số ![]() là:
là:
Ta có:
Lẫy ngẫu nhiên 5 viên bi trong hộp có 13 viên bi gồm 6 bi xanh, 7 bi đỏ. Tính xác suất để 5 viên bi lấy được có số bi xanh nhiều hơn số bi đỏ?
Gọi A là biến cố lấy số bi xanh nhiều hơn bi đỏ
Khi đó ta có:
TH1: lấy được 5 viên bi xanh cách
TH2: lấy được 4 viên bi xanh; 1 viên bi đỏ cách
TH3: lấy được 3 viên bi xanh; 2 viên bi đỏ cách
Do đó xác suất của biến cố A là:
Cho hình chóp ![]() có đáy là hình thoi tâm
có đáy là hình thoi tâm ![]() . Biết rằng
. Biết rằng ![]() . Hãy chọn kết luận sai dưới đây?
. Hãy chọn kết luận sai dưới đây?
Hình vẽ minh họa
Ta có tam giác SAC cân tại S và SO là đường trung tuyến cũng đồng thời là đường cao
=>
Trong tam giác SOA thì AC và SA không thể vuông tại A
Vậy khẳng định sai là: .
Cho các số thực a và b thỏa mãn ![]() . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?
Điều kiện để các căn thức có nghĩa là
Ta có:
Xét hiệu
Vì nên
Từ đó ta có:
Từ (*) và (**) suy ra
Cho bất phương trình ![]() . Xác định nghiệm của bất phương trình đã cho?
. Xác định nghiệm của bất phương trình đã cho?
Ta có:
Vậy tập nghiệm của bất phương trình là
Có bao nhiêu giá trị nguyên của dương của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên tập số thực?
đồng biến trên tập số thực?
Đáp án: 4
Có bao nhiêu giá trị nguyên của dương của tham số để hàm số
đồng biến trên tập số thực?
Đáp án: 4
Hàm số đồng biến trên
khi và chỉ khi
Mà
Vậy có 4 giá trị của tham số m thỏa mãn điều kiện đề bài.
Cho tứ diện S.ABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác SBC đều, tam giác ABC vuông tại A. Gọi H, I lần lượt là trung điểm của BC và AB. Khẳng định nào sau đây sai?
Hình vẽ minh họa:
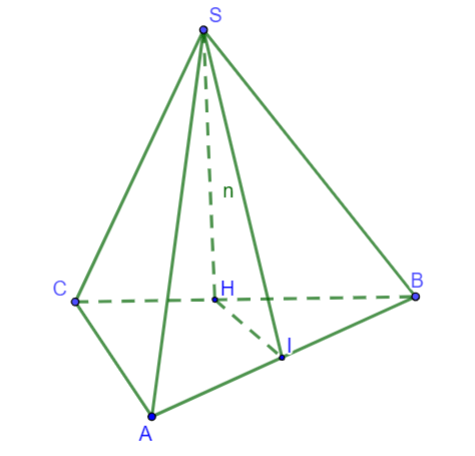
Ta có: SBC là tam giác đều có H là trung điểm BC nên
Mà (SBC)⊥(ABC) theo giao tuyến BC
=> đúng.
Ta có HI là đường trung bình của ΔABC nên
=> đúng.
Ta có
=> đúng
Có bao nhiêu cách chọn một tổ tưởng tổ dân phố từ một nhóm cư dân gồm 25 nam và 20 nữ?
Số cách chọn một người từ 45 người là: (cách)
Vậy có 45 cách chọn tổ trưởng tổ dân phố.
Hình chóp tam giác đều ![]() . Gọi
. Gọi ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có khối chóp tam giác đều có đáy
là tam giác đều, trọng tâm G cũng là tâm của đáy nên
.
Đặt ![]() . Hãy biểu diễn
. Hãy biểu diễn ![]() theo a và b.
theo a và b.
Ta có:
Bà A gửi ngân hàng 100 triệu đồng vào ngân hàng với lãi suất 10%/ 1 năm theo hình thức lại kép một thời gian dài (nghĩa là nếu bà không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo). Năm nay gia đình có việc cần nên bà rút hết tiền trong ngân hàng để xử lí công việc. Sau khi rút cả vốn và lãi, bà trích ra 10 triệu để mua đồ tân gia cho con trai thì bà còn 240 triệu. Hỏi bà A đã gửi tiết kiệm được bao nhiêu năm? 10 năm||12 năm||20 năm||15 năm
Bà A gửi ngân hàng 100 triệu đồng vào ngân hàng với lãi suất 10%/ 1 năm theo hình thức lại kép một thời gian dài (nghĩa là nếu bà không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo). Năm nay gia đình có việc cần nên bà rút hết tiền trong ngân hàng để xử lí công việc. Sau khi rút cả vốn và lãi, bà trích ra 10 triệu để mua đồ tân gia cho con trai thì bà còn 240 triệu. Hỏi bà A đã gửi tiết kiệm được bao nhiêu năm? 10 năm||12 năm||20 năm||15 năm
Giả sử bà A đã gửi ngân hàng trong x năm
Số tiền bà nhận được là 250 triệu đồng
Áp dụng công thức lại kép thì sau n năm số tiền bà A nhận được là
Vậy bà A đã gửi tiết kiệm trong 10 năm.
Cho 4 chữ số ![]() có thể lập được bao nhiêu chữ số biết rằng các số tạo thành thuộc khoảng
có thể lập được bao nhiêu chữ số biết rằng các số tạo thành thuộc khoảng ![]() ?
?
Gọi số cần tìm có dạng với
.
Theo giả thiết ta có hai cách chọn a
Với mỗi cách chọn a ta có 4 cách chọn b và 4 cách chọn x.
Vậy có số thỏa mãn yêu cầu đề bài.
Cho hình chóp ![]() có
có ![]() là hình vuông cạnh
là hình vuông cạnh ![]() , tam giác
, tam giác ![]() đều. góc giữa
đều. góc giữa ![]() và
và ![]() là:
là:
Hình vẽ minh họa
Vì
Quản lí xưởng kiểm tra 4 sản phẩm trong kho gồm hai loại là đạt và không đạt. Gọi ![]() là biến cố sản phẩm được kiểm tra lần thứ
là biến cố sản phẩm được kiểm tra lần thứ ![]() thuộc loại không đạt,
thuộc loại không đạt, ![]() . Mô tả nào sau đây mô tả đúng biến cố chỉ có một sản phẩm thuộc loại đạt qua các
. Mô tả nào sau đây mô tả đúng biến cố chỉ có một sản phẩm thuộc loại đạt qua các ![]() ?
?
Mô tả đúng là:
Một hộp đựng 8 viên bi màu xanh, 5 viên bi đỏ, 3 viên bi màu vàng. Có bao nhiêu cách chọn từ hộp đó ra 4 viên bi trong đó có đúng 2 viên bi xanh?
Trong 4 viên bi có đúng 2 viên bi màu xanh
=> 2 viên bi còn lại nằm trong 8 viên bi (màu đỏ và màu vàng)
=> Số cách chọn 4 viên bi trong đó có đúng 2 viên bi xanh là: cách
Ba bạn A, B, C độc lập với nhau thi ném phi tiêu vào cùng một bia. Biết xác xuất ném trúng của A, B, C lần lượt là ![]() và
và ![]() . Tính xác suất để có ít nhất một người ném trúng bia?
. Tính xác suất để có ít nhất một người ném trúng bia?
Gọi A, B, C tương ứng là biến cố A ném trúng bia, B ném trúng bia và C ném trúng bia
A, B, C là các biến cố độc lập. Do đó A, B, C là các biến cố đôi một độc lập
Xác suất để cả ba người đều không ném trúng là:
Gieo một con xúc xắc cân đối và đồng chất 2 lần liên tiếp. Giả sử N là biến cố “Có ít nhất một mặt 6 chấm xuất hiện” Mô tả nào sau đây đúng khi mô tả biến cố N?
Mô tả đúng biến cố N là:
Phương trình chuyển động của một chất điểm được biểu diễn ![]() ,
, ![]() tính bằng giây,
tính bằng giây, ![]() tính bằng mét. Tại thời điểm
tính bằng mét. Tại thời điểm ![]() thì gia tốc tức thời của chất điểm bằng bao nhiêu?
thì gia tốc tức thời của chất điểm bằng bao nhiêu?
Gọi gia tốc của chuyển động tính theo thời gian t là a(t) ta có:
Gia tốc tức thời tại thời điểm t = 2s là
Tính giá trị biểu thức: ![]() . Biết
. Biết ![]() là các số thực dương khác 1 và thỏa mãn
là các số thực dương khác 1 và thỏa mãn ![]() ?
?
Ta có:
Lại có
Trong các mệnh đề sau, mệnh đề nào sai?
Trong trường hợp a và b vuông góc nhau và chéo nhau, nếu (P) ⊃ a, (P) // b và (Q) ⊃ b, (Q) // a thì (P) // (Q).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a. Giả sử góc BAD bằng 600. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng:
Hình vẽ minh họa
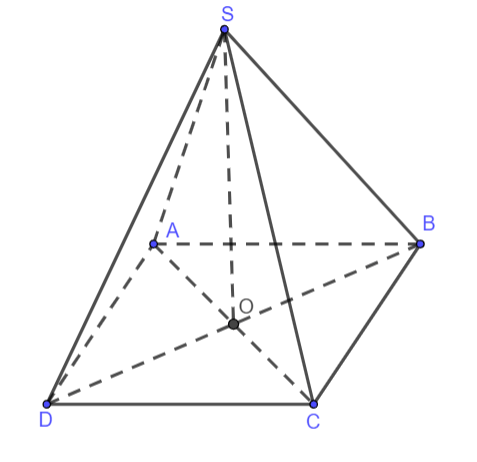
Từ S vẽ SO ⊥ (ABCD) ⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau) ⇒ O là tâm đường tròn ngoại tiếp đáy
Giả sử ![]() là tổng các nghiệm của phương trình
là tổng các nghiệm của phương trình ![]() . Giá trị của
. Giá trị của ![]() là:
là:
Điều kiện xác định
Phương trình đã cho tương đương:
Cho khối chóp ![]() có
có ![]() biết độ dài các cạnh
biết độ dài các cạnh ![]()
![]() . Thể tích khối chóp
. Thể tích khối chóp ![]() là:
là:
Hình vẽ minh họa
Ta có:
Nên tam giác ABC vuông tại A
Suy ra
Vậy
Cho hình lăng trụ đứng tam giác ![]() có đáy
có đáy ![]() là tam giác cân,
là tam giác cân, ![]() và cạnh bên
và cạnh bên ![]() . Tính góc giữa hai đường thẳng
. Tính góc giữa hai đường thẳng ![]() và
và ![]() ?
?
Hình vẽ minh họa
Ta có:
Xét tam giác ta có:
Áp dụng định lí cosin cho tam giác ABC ta có:
Vậy tam giác đều
Viết phương trình tiếp tuyến của đồ thị hàm số ![]() . Biết
. Biết ![]() song song với đường thẳng
song song với đường thẳng ![]() ?
?
Gọi là tiếp điểm của tiếp tuyến
Ta có:
Do song song với đường thẳng
nên
Với nên phương trình tiếp tuyến tương ứng là
Với nên phương trình tiếp tuyến tương ứng là
Hàm số nào sau đây phù hợp với hình vẽ:

Ta có: và hàm số đồng biến trên
nên chỉ có hàm số
thỏa mãn.
Cho hình lập phương ![]() . Giả sử mặt phẳng
. Giả sử mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() vuông góc với
vuông góc với ![]() . Thiết diện tạo bởi
. Thiết diện tạo bởi ![]() và hình lập phương là:
và hình lập phương là:
Hình vẽ minh họa
Ta có:
Vậy chính là mặt phẳng
. Thiết diện là một hình chữ nhật.
Cấu trúc đề thi cuối học kì I môn Vật lí gồm 50 câu trắc nghiệm, mỗi câu có 4 đáp án trắc nghiệm và chỉ có duy nhất 1 đáp án đúng. Mỗi câu trả lời đúng được 0,2 điểm. Học sinh A chọn ngẫu nhiên đáp án cho các câu hỏi. Xác suất để học sinh A thi được 6 điểm môn Vật lí là:
Để đạt được điểm 6 học sinh đó cần trả lời đúng 30 câu và trả lời sai 20 câu.
Theo đó xác suất trả lời đúng 1 câu là 0,25, xác suất trả lời sai mỗi câu là 0,75
Vậy xác suất để học sinh đạt 6 điểm là: .
