Cho bất phương trình ![]() (1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
(1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
Để thì
nghiệm đúng với
.
Nghĩa là:
Cho bất phương trình ![]() (1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
(1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
Để thì
nghiệm đúng với
.
Nghĩa là:
Một bình chứa ![]() viên bi màu, trong đó có
viên bi màu, trong đó có ![]() bi xanh,
bi xanh, ![]() bi đỏ,
bi đỏ, ![]() bi trắng. Lấy ngẫu nhiên
bi trắng. Lấy ngẫu nhiên ![]() viên bi từ bình đó. Tính xác suất để lấy được
viên bi từ bình đó. Tính xác suất để lấy được ![]() viên bi khác màu.
viên bi khác màu.
Lấy viên bi bất kì trong
viên bi trong bình thì có
(cách).
Lấy viên bi cùng màu thì có
(cách) nên có
(cách) lấy được
viên bi khác màu.
Xác suất để lấy được viên bi khác màu trong tổng số
viên bi là
.
Có bao nhiêu cách xếp 8 người vào một bàn tròn?
Vì xếp vào bàn tròn nên vị trí xếp đầu tiên là như nhau nên có 1 cách xếp, ta xếp 7 người còn lại vào 7 vị trí nên có 7! cách xếp.
Vậy có 1.7! = 5040 cách xếp
Cho tam thức bậc hai f(x) = 5x − x2 − 6. Tìm x để f(x) ≥ 0.

Dựa vào bảng xét dấu, ta chọn đáp án x ∈ [2; 3].
Cho dường tròn ![]() và đường thẳng
và đường thẳng ![]() . Biết rằng các tiếp tuyến của
. Biết rằng các tiếp tuyến của ![]() tạo với đường thẳng
tạo với đường thẳng ![]() một góc
một góc ![]() với
với ![]() tạo thành một đa giác. Chu vi của đa giác là:
tạo thành một đa giác. Chu vi của đa giác là:
Đường tròn (C) có tâm I(1; -2) bán kính r = 5
Gọi là tiếp tuyến của
. Gọi
là một vectơ pháp tuyến của
.
thấy
Khi thì ta chọn
. Khi đó, ta được
. Do
là tiếp tuyến của
nên ta có
Lúc đó, ta có .
Khi thì ta chọn
. Khi đó, ta được
.
Do là tiếp tuyến của
nên ta có:
.
Lúc đó, ta có .
Ta thấy 4 tiếp tuyến này tạo thành hình thoi , với tọa độ của
là nghiệm của hệ
hay
.
Tọa độ của là nghiệm của hệ phương trình
hay
.
Tọa độ của là nghiệm của hệ phương trình:
hay
.
Ta được nên chu vi của hình thoi
sẽ bằng
.
Tìm hàm số bậc hai trong các hàm số dưới đây?
Theo định nghĩa ta có:
Hàm số bậc hai là .
Một tổ có 10 học sinh. Hỏi có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó.
Số cách chọn hai học sinh từ 10 học sinh là chỉnh hợp chập 2 của 10 phần tử
=> Số cách chọn là: (cách)
Cho tập hợp ![]() . Chọn ngẫu nhiên ba số từ tập đó. Tính xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.
. Chọn ngẫu nhiên ba số từ tập đó. Tính xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.
Số phần tử không gian mẫu là .
Gọi là biến cố “Ba số chọn ra không có hai số nào là hai số nguyên liên tiếp”.
là biến cố “Ba số được chọn có ít nhất hai số là các số tự nhiên liên tiếp”.
+ Bộ ba số dạng , với
: có
bộ ba số.
+ Bộ ba số có dạng , với
: có
bộ ba số.
+ Tương tự mỗi bộ ba số dạng ,
,
,
,
,
,
đều có
bộ.
.
.
Trong các phương trình sau đây, phương trình nào là phương trình chính tắc của Hypebol?
Phương trình Hypebol có dạng
Vậy phương trình cần tìm là .
Tìm số hạng chứa ![]() trong khai triển
trong khai triển ![]() ?
?
Số hạng tổng quát theo thứ tự giảm dần số mũ x là:
Số hạng chứa ứng với
Số hạng cần tìm là .
Trong mặt phẳng tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]() và
và ![]() . Tìm giá trị của tham số
. Tìm giá trị của tham số ![]() để hai đường thẳng vuông góc với nhau?
để hai đường thẳng vuông góc với nhau?
Ta có:
Hai đường thẳng vuông góc với nhau khi và chỉ khi:
Vậy hai đường thẳng vuông góc với nhau khi và chỉ khi .
Trên hệ trục tọa độ cho đường tròn ![]() . Trong các điểm sau điểm nào nằm trên đường tròn đã cho?
. Trong các điểm sau điểm nào nằm trên đường tròn đã cho?
Thay tọa độ điểm vào phương trình đường tròn
ta được:
Vậy điểm thuộc đường tròn là .
Kí hiệu nào sau đây là kí hiệu của biến cố chắc chắn?
Kí hiệu biến cố chắc chắn là Ω.
Viết phương trình tham số của đường thẳng đi qua hai điểm ![]() và
và ![]() .
.
Ta có:
Cho phương trình ![]() . Số nghiệm của phương trình này là:
. Số nghiệm của phương trình này là:
ĐKXĐ: x > 2 khi đó phương trình trở thành .
Đối chiếu điều kiện suy ra phương trình có một nghiệm x = 4.
Cho đường tròn ![]() và đường thẳng
và đường thẳng ![]() . Tìm phương trình tiếp tuyến của
. Tìm phương trình tiếp tuyến của ![]() song song với đường thẳng
song song với đường thẳng ![]() ?
?
Ta có: Phương trình đường tròn (C) có tâm I(2; 3) bán kính R = 5
Phương trình đường thẳng song song với d có dạng
tiếp xúc với
nên
Hay
Vậy phương trình tiếp tuyến của song song với
là:
hoặc
.
Thí nghiệm nào không phải là phép thử ngẫu nhiên?
Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.
Đáp án “Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.” không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể số bi xanh và số bi đỏ.
Xác định m để biểu thức ![]() là tam thức bậc hai.
là tam thức bậc hai.
Để biểu thức là tam thức bậc hai ta có:
Có tất cả bao nhiêu số hạng trong khai triển nhị thức Newton của ![]() ?
?
Khi viết nhị thức dưới dạng khai triển
số hạng.
Nhận xét nào đúng về vị trí tương đối của hai đường thẳng ![]() và
và ![]() ?
?
Ta có:
Vectơ pháp tuyến của đường thẳng là:
Vectơ pháp tuyến của đường thẳng là:
Suy ra và
không cùng phương và
Suy ra hai đường thẳng cắt nhau và không vuông góc.
Khoảng cách từ điểm M( –1; 1) đến đường thẳng ∆: 3x – 4y – 3 = 0 bằng:
Ta có: .
Trong các phương trình sau, phương trình nào là phương trình đường tròn?
Phương trình có dạng
với
Ta có:
Vậy phương trình không là phương trình đường tròn.
Phương trình có dạng
với
Ta có:
Vậy phương trình không là phương trình đường tròn.
Ta có:
Vậy đường tròn có bán kính và bán kính
Phương trình không phải là phương trình đường tròn vì hệ số của
khác nhau.
Có thể lập được bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau?
Gọi số tự nhiên có ba chữ số có dạng
Có 9 cách chọn a
Có 9 cách chọn b
Có 8 cách chọn c
=> Số các số được tạo thành là: số.
Một đường thẳng có vectơ chỉ phương là ![]() . Vectơ nào sau đây là vectơ pháp tuyến của
. Vectơ nào sau đây là vectơ pháp tuyến của ![]() ?
?
Ta có:
Đường thẳng có vectơ chỉ phương
thì sẽ có một vectơ pháp tuyến là:
Áp dụng vào bài toán ta được:
Vectơ pháp tuyến của là:
.
Cho các chữ số ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Từ các chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có
. Từ các chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có ![]() chữ số và các chữ số đôi một bất kỳ khác nhau?
chữ số và các chữ số đôi một bất kỳ khác nhau?
Gọi số cần tìm là: (với
,
).
Trường hợp 1:
Chọn , nên có
cách chọn.
Chọn nên có
cách chọn.
Chọn có
cách chọn.
Chọn có
cách chọn.
Suy ra, có số.
Trường hợp 2:
Chọn , nên có
cách chọn.
Chọn nên có
cách chọn.
Chọn có
cách chọn.
Chọn có
cách chọn.
Suy ra, có số.
Vậy có tất cả: số.
Biết rằng ![]() . Chọn kết luận đúng?
. Chọn kết luận đúng?
Thay vào
ta được:
Có ![]() học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc trong đó khối
học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc trong đó khối ![]() có
có ![]() học sinh nam và
học sinh nam và ![]() học sinh nữ, khối
học sinh nữ, khối ![]() có
có ![]() học sinh nam. Chọn ngẫu nhiên
học sinh nam. Chọn ngẫu nhiên ![]() học sinh bất kỳ để trao thưởng, xác suất để
học sinh bất kỳ để trao thưởng, xác suất để ![]() học sinh được có cả nam và nữ đồng thời có cả khối
học sinh được có cả nam và nữ đồng thời có cả khối ![]() và khối
và khối ![]() là bao nhiêu?
là bao nhiêu?
Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là .
Gọi là biến cố
học sinh được ó cả nam và nữ đồng thời có cả khối
và khối
. Ta có các trường hợp thuận lợi cho biến cố
là:
TH1: Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có cách.
TH2: Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có cách.
TH3: Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có cách.
Suy ra số phần tử của biến cố là
.
Vậy xác suất cần tính
Một bài trắc nghiệm khách quan có 10 câu hỏi. Mỗi câu hỏi có 4 phương án trả lời. Có bao nhiêu phương án trả lời?
Mỗi câu hỏi có 4 cách chọn phương án trả lời.
Mười câu hỏi sẽ có số cách chọn phương án trả lời là 410.
Gieo một đồng tiền liên tiếp 3 lần. Xác suất của biến cố ![]() : "có đúng 2 lần xuất hiện mặt sấp" là bao nhiêu?
: "có đúng 2 lần xuất hiện mặt sấp" là bao nhiêu?
Chọn 2 trong 3 lần để xuất hiện mặt sấp có cách.
2 lần xuất hiện mặt sấp có xác suất mỗi lần là . Lần xuất hiện mặt ngửa có xác suất là
.
Vậy: .
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
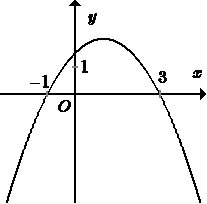
Nhận xét:
Parabol có bề lõm hướng xuống.
Parabol cắt trục hoành tại 2 điểm (3;0) và (−1;0). Xét các đáp án, đáp án thỏa mãn.
Chọn đáp án đúng khi khai triển nhị thức ![]() ?
?
Ta có:
Đạt và Phong tham gia chơi trò một trò chơi đối kháng, thỏa thuận rằng ai thắng 5 ván trước là thắng chung cuộc và được hưởng toàn bộ số tiền thưởng của chương trình (không có ván nào hòa). Tuy nhiên khi Đạt thắng được 4 ván và Phong thắng được 2 ván rồi thì xảy ra sự cố kĩ thuật và chương trình buộc phải dừng lại. Biết rằng giới chuyên môn đánh giá Phong và Đạt ngang tài ngang sức. Hỏi phải chia số tiền thưởng như thế nào cho hợp lý (dựa trên quan điểm tiền thưởng tỉ lệ thuận với xác suất thắng cuộc của mỗi người).
Phân tích: Đề bài cho các điều kiện khá dài dòng, ta cần đưa chúng về dạng ngắn gọn dễ hiểu hơn.
+) “Biết rằng giới chuyên môn đánh giá Phong và Đạt ngang tài ngang sức”: xác suất để Phong và Đạt thắng trong một ván là như nhau và bằng .
+) “Khi Đạt thắng được 4 ván và Phong thắng được 2 ván rồi”: nghĩa là Đạt chỉ cần thắng một ván nữa là được 5 ván, còn Phong phải thắng 3 ván nữa mới đạt được.
Để xác định xác suất thắng chung cuộc của Đạt và Phong ta tiếp tục chơi thêm các ván “giả tưởng”. Để Phong có thể thắng chung cuộc thì anh phải thắng Đạt 3 ván liên tiếp (vì Đạt chỉ còn một ván nữa là thắng).
Như vậy xác suất thắng cuộc của Phong là: .
Xác suất thắng cuộc của Đạt là .
Vậy Tỉ lệ chia tiền phù hợp là .
Viết tập hợp Ω là không gian mẫu trong trò chơi tung đồng xu hai lần liên tiếp.
Ta có: Ω = {SS; SN; NS; NN}.
Tìm tập xác định D của hàm số ![]()
Điều kiện .
Vậy tập xác định của hàm số là .
Với ![]() là số nguyên dương thỏa mãn
là số nguyên dương thỏa mãn ![]() . Trong khai triển biểu thức
. Trong khai triển biểu thức ![]() , gọi
, gọi ![]() là số hạng mà tổng số mũ của
là số hạng mà tổng số mũ của ![]() và
và ![]() của số hạng đó bằng
của số hạng đó bằng ![]() . Hệ số của
. Hệ số của ![]() là :
là :
Điều kiện: ,
.
Ta có
.
.
.
Ta có: . Vậy hệ số
.
Xác định góc giữa hai đường thẳng ![]() và
và ![]() ?
?
Ta có:
Một Elip đi qua điểm ![]() và có độ dài trục lớn là
và có độ dài trục lớn là ![]() . Hãy xác định phương trình chính tắc của elip đó?
. Hãy xác định phương trình chính tắc của elip đó?
Phương trình chính tắc của elip có dạng
Do (E) có độ dài trục lớn là nên
Do (E) đi qua điểm nên
Vậy phương trình chính tắc của elip là: .
Trong mặt phẳng tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]() . Phương trình tổng quát của đường trung tuyến kẻ từ đỉnh
. Phương trình tổng quát của đường trung tuyến kẻ từ đỉnh ![]() của tam giác
của tam giác ![]() là:
là:
Gọi I là trung điểm của AC. Ta có:
Đường trung tuyến BI đi qua điểm B và nhận làm vectơ chỉ phương nên có vectơ pháp tuyến
.
Phương trình tổng quát của đường thẳng là:
Tất cả các giá trị của tham số m để phương trình ![]() có nghiệm là:
có nghiệm là:
ĐKXĐ x > − 1
pt ⇔ 3mx + 1 + x + 1 = 2x + 5m + 3 ⇔ (3m−1)x = 5m + 1.
Phương trình đã cho có nghiệm .
