Tập nghiệm ![]() của phương trình
của phương trình ![]() là:
là:
Ta có: .
Thử lại thấy không thỏa mãn.
Vậy .
Tập nghiệm ![]() của phương trình
của phương trình ![]() là:
là:
Ta có: .
Thử lại thấy không thỏa mãn.
Vậy .
Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ ba có 6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào lọ hoa, tính xác suất để trong 7 hoa được có số hoa hồng bằng số hoa ly.
Không gian mẫu là số cách chọn ngẫu nhiên 7 hoa từ ba bó hoa gồm 21 hoa.
Suy ra số phần tử của không gian mẫu là .
Gọi là biến cố
7 hoa được ó số hoa hồng bằng số hoa ly
. Ta có các trường hợp thuận lợi cho biến cố
là:
TH1: Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có cách.
TH2: Chọn 2 hoa hồng, 2 hoa ly và 3 hoa huệ nên có cách.
TH3: Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có cách.
Suy ra số phần tử của biến cố là
.
Vậy xác suất cần tính
Cho đường tròn ![]() và đường thẳng
và đường thẳng ![]() . Tìm giá trị của tham số m để
. Tìm giá trị của tham số m để ![]() không cắt
không cắt ![]() ?
?
Đường tròn (C) có tâm I(1; 2) và
Để không cắt
thì
Vậy thỏa mãn yêu cầu bài toán.
Viết phương trình tham số của đường thẳng ![]() có phương trình
có phương trình ![]() ?
?
Đường thẳng đi qua điểm
và có vectơ pháp tuyến là
nên có vectơ chỉ phương là:
.
Vậy phương trình tham số của là:
.
Số giá trị nguyên của x để tam thức f(x) = 2x2 − 7x − 9 nhận giá trị âm là
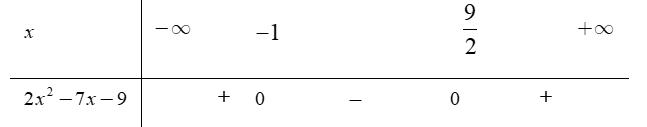
Dựa vào bảng xét dấu, .
Mà x ∈ ℤ⇒ x ∈ {0;1;2;3;4} (5 giá trị).
Chọn ngẫu nhiên 3 số tự nhiên từ tập hợp ![]() . Xác suất của
. Xác suất của ![]() để trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp bằng bao nhiêu?
để trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp bằng bao nhiêu?
Có tất cả cách chọn 3 số tự nhiên từ tập hợp
.
Suy ra .
Xét biến cố “Chọn 3 số tự nhiên sao cho không có 2 số tự nhiên liên tiếp”.
Ta có “Chọn 3 số tự nhiên sao luôn có 2 số tự nhiên liên tiếp”.
Xét các trường hợp sau:
+ Trường hợp 1: Trong ba số chọn được chỉ có 2 số liên tiếp:
- Nếu 2 số liên tiếp là hoặc
thì số thứ ba có
cách chọn (do không tính số liên tiếp sau và trước mỗi cặp số đó).
- Nếu 2 số liên tiếp là ,
,.,
thì số thứ ba có
cách chọn (do không tính 2 số liền trước và sau mỗi cặp số đó).
Trường hợp này có cách chọn.
+ Trường hợp 2: Chọn được 3 số liên tiếp.
Tức là chọn các bộ ,
,.,
: có tất cả 2017 cách.
Suy ra .
Vậy .
Tính giá trị biểu thức ![]()
Áp dụng công thức cho
ta có:
Tìm m để đường thẳng ![]() và
và ![]() tạo với nhau một góc
tạo với nhau một góc ![]() ?
?
Ta có:
Vectơ pháp tuyến của đường thẳng là:
Vectơ pháp tuyến của đường thẳng là:
Hai đường thẳng vuông góc với nhau khi và chỉ khi:
Vậy hai đường thẳng vuông góc với nhau khi và chỉ khi .
Xếp ngẫu nhiên 5 bạn nam và 3 bạn nữ vào một bàn tròn. Xác suất để không có ba bạn nữ nào ngồi cạnh nhau.
Theo công thức hoán vị vòng quanh ta có:
Để xếp các bạn nữ không ngồi cạnh nhau, trước hết ta xếp các bạn nam vào bàn tròn: có cách, giữa 5 bạn nam đó ta sẽ có được 5 ngăn (do ở đây là bàn tròn). Xếp chỉnh hợp 3 bạn nữ vào 5 ngăn đó có
cách.
Vậy xác suất xảy ra là:.
Các giá trị m làm cho biểu thức ![]() luôn dương là
luôn dương là
Biểu thức luôn dương
Công thức nào dưới đây là công thức tính khoảng cách từ một điểm ![]() đến đường thẳng
đến đường thẳng ![]() ?
?
Công thức tính khoảng cách từ một điểm đến đường thẳng
là:
Một hộp có ![]() bi đen,
bi đen, ![]() bi trắng. Chọn ngẫu nhiên
bi trắng. Chọn ngẫu nhiên ![]() bi. Tính xác suất
bi. Tính xác suất ![]() bi được chọn có đủ hai màu.
bi được chọn có đủ hai màu.
Số phần tử không gian mẫu: .
(bốc 2 bi bất kì từ 9 bi trong hộp ).
Gọi : “hai bi được chọn có đủ hai màu”. Ta có:
.
( chọn 1 bi đen từ 5 bi đen – chọn 1 bi trắng từ 4 bi trắng ).
Khi đó: .
Trong mặt phẳng tọa độ ![]() , cho tọa độ điểm
, cho tọa độ điểm ![]() và hai đường thẳng
và hai đường thẳng ![]() ;
; ![]() . Một đường tròn
. Một đường tròn ![]() có tâm
có tâm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() , đi qua điểm
, đi qua điểm ![]() và tiếp xúc với
và tiếp xúc với ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Ta có:
Lại có đường tròn tâm I đi qua P và tiếp xúc với đường thẳng nên
Vậy khẳng định đúng là: .
Phát biểu nào sau đây đúng?
Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.
Phương trình tham số của đường thẳng ![]() đi qua hai điểm
đi qua hai điểm ![]() và
và ![]() là:
là:
Phương trình tham số của đường thẳng AB đi qua điểm và nhận
làm vectơ chỉ phương.
Vậy phương trình cần tìm là: .
Hoạt động nào sau đây không phải là phép thử?
Các hoạt động ở các phương án:
" Chọn một trong ba bạn An, Bình, Cường tham gia cuộc thi chạy điền kinh."
"Chơi trò chơi gắp thú nhồi bông."
"Chọn một quyển sách bất kì trên giá sách và đọc tên của quyển sách đó."
Đều là phép thử vì ta không thể đoán trước được kết quả của hoạt động đó mặc dù biết được tất cả các kết quả có thể xảy ra.
Hoạt động ở phương án A không phải là phép thử vì ta có thể đoán trước được kết quả của hoạt động đó là: 2 + 5 + 3 = 10 (chiếc bút bi).
Trong mặt phẳng hệ trục tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() cắt hai trục
cắt hai trục ![]() lần lượt tại điểm
lần lượt tại điểm ![]() với
với ![]() . Khi đó phương trình đường thẳng
. Khi đó phương trình đường thẳng ![]() là:
là:
Phương trình đường thẳng d là: .
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
Vậy tập nghiệm của bất phương trình là:
Xét phép thử tung con súc sắc 6 mặt hai lần. Xác định số phần tử của không gian mẫu.
Không gian mẫu gồm các bộ , trong đó
.
nhận 6 giá trị,
cũng nhận 6 giá trị nên có
bộ
.
Vậy và
.
Gieo một con xúc xắc cân đối đồng chất 2 lần. Tính xác suất để biến cố có tích 2 lần số chấm khi gieo xúc xắc là một số chẵn.
Số phần tử của không gian mẫu là
Gọi là biến cố
Tích hai lần số chấm khi gieo xúc xắc là một số chẵn
. Ta xét các trường hợp:
TH1:. Gieo lần một, số chấm xuất hiện trên mặt là số lẻ thì khi gieo lần hai, số chấm xuất hiện phải là số chẵn. Khi đó có cách gieo.
TH2:. Gieo lần một, số chấm xuất hiện trên mặt là số chẵn thì có hai trường hợp xảy ra là số chấm xuất hiện trên mặt khi gieo lần hai là số lẻ hoặc số chẵn. Khi đó có cách gieo.
Suy ra số kết quả thuận lợi cho biến cố là
Vậy xác suất cần tìm tính
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x + 3y + 5 = 0 và A(1; –3). Khoảng cách từ điểm A đến đường thẳng d là:
Ta có: .
Khai triển biểu thức ![]() ta thu được kết quả:
ta thu được kết quả:
Ta có:
Khai triển ![]() thành đa thức ta được biểu thức gồm mấy số hạng?
thành đa thức ta được biểu thức gồm mấy số hạng?
Biểu thức khai triển thành đa thức có 5 hạng tử.
Cho tam giác ![]() nội tiếp đường tròn
nội tiếp đường tròn ![]() . Gọi
. Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên cạnh
trên cạnh ![]() . Đường tròn đường kính
. Đường tròn đường kính ![]() cắt
cắt ![]() lần lượt tại
lần lượt tại ![]() . Biết đường thẳng chứa
. Biết đường thẳng chứa ![]() có phương trình
có phương trình ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() ?
?
Hình vẽ minh họa
Do tam giác ABC vuông tại A và nội tiếp đường tròn (C) nên (C) là đường tròn đường kính BC (tâm I(3; 1) là trung điểm của BC.
Đường tròn đường kính AH cắt AB và AC lần lượt tại M và N nên
Ta có:
Do đó AI có phương trình
Ta có:
Suy ra phương trình AI là
Mà nên ta có tọa độ điểm A thỏa mãn hệ phương trình:
Nếu khi đó
khi đó A và I nằm cùng phía đối với đường thẳng MN nên không thỏa mãn yêu cầu đề bài.
Vậy tọa độ điểm A là
Tại khu vực giá sách tham khảo lớp 11 có 20 sách tham khảo môn Toán khác nhau, 40 sách tham khảo môn Vật lý khác nhau và 50 quyển sách tham khảo môn Hóa học khác nhau. Hỏi có bao nhiêu cách chọn một quyển sách trên giá sách?
Số cách chọn sách Toán là 20 cách.
Số cách chọn sách Vật lí là 40 cách.
Số cách chọn sách Hóa học là 50 cách.
Vậy để chọn một cuốn sách trên giá sách ta có 20 + 40 + 50 = 110 cách chọn.
Phương trình đường tròn ![]() có tâm và bán kính lần lượt là:
có tâm và bán kính lần lượt là:
Ta có:
Vậy phương trình đường tròn đã cho có tâm và bán kính lần lượt là:
Cho đường thẳng ![]() và đường thẳng
và đường thẳng ![]() . Tính góc hợp bởi hai đường thẳng?
. Tính góc hợp bởi hai đường thẳng?
Vectơ chỉ phương của là:
Vectơ chỉ phương của là:
Ta có:
Vậy góc hợp bởi hai đường thẳng đã cho bằng .
Phương trình ![]() có mấy nghiệm nguyên ?
có mấy nghiệm nguyên ?
Đặt . Phương trình đã cho trở thành:
Vậy phương trình có 0 nghiệm nguyên.
Có thể lập được bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau?
Gọi số tự nhiên có ba chữ số có dạng
Có 9 cách chọn a
Có 9 cách chọn b
Có 8 cách chọn c
=> Số các số được tạo thành là: số.
Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Hàm số bậc hai y = x2 – 3x + 2 có tập xác định là ℝ. Khẳng định "Tập xác định của hàm số là D = (0; +∞)." sai.
Xét điểm M(1; 0): thay x = 1; y = 0 vào hàm số ta có: 0 = 12 – 3. 1 + 2 = 0 là mệnh đề đúng. Vậy M(1; 0) thuộc đồ thị hàm số. Khẳng định "Điểm M(1; 0) thuộc đồ thị hàm số." đúng.
Hàm số y = x2 – 3x + 2 có a = 1 > 0, b = ‒3 nên hàm số nghịch biến trên khoảng và đồng biến trên khoảng
. Khẳng định "Hàm số đồng biến trên ℝ." sai.
Hàm số y = x2 – 3x + 2 có a = 1 > 0 nên đồ thị hàm số có bề lõm quay lên trên. Khẳng định "Đồ thị hàm số có bề lõm quay xuống dưới." sai.
Cho phương trình đường tròn ![]() . Viết phương trình tiếp tuyến của đường tròn
. Viết phương trình tiếp tuyến của đường tròn ![]() biết rằng tiếp tuyến vuông góc với đường thẳng
biết rằng tiếp tuyến vuông góc với đường thẳng ![]() ?
?
Đường tròn (C) có tâm
Vì vuông góc với đường thẳng
nên phương trình
có dạng
Vì là tiếp tuyến của (C) nên ta có:
Với thì phương trình
là
Với thì phương trình
là
Từ các chữ số ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() có thể lập được bao nhiêu số tự nhiên gồm
có thể lập được bao nhiêu số tự nhiên gồm ![]() chữ số đôi một khác nhau trong đó hai chữ số
chữ số đôi một khác nhau trong đó hai chữ số ![]() và
và ![]() không đứng cạnh nhau.
không đứng cạnh nhau.
Số các số có chữ số được lập từ các chữ số
,
,
,
,
,
là
.
Số các số có chữ số và
đứng cạnh nhau:
.
Số các số có chữ số và
không đúng cạnh nhau là:
.
Tổng các nghiệm của phương trình ![]() là bao nhiêu?
là bao nhiêu?
.
Vậy tổng các nghiệm của phương trình là .
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Ta có:
Vậy phương trình đường tròn cần tìm là: .
Cho ![]() là số thực dương, số hạng không chứa
là số thực dương, số hạng không chứa ![]() trong khai triển nhị thức
trong khai triển nhị thức ![]() là:
là:
Ta có
Số hạng tổng quát thứ trong khai triển là
.
Số hạng này không chứa tương ứng với trường hợp
.
Vậy số hạng không chứa trong khai triển là
.
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Hệ số góc
. Hệ số góc ![]() của đường thẳng
của đường thẳng ![]() là:
là:
Ta có:
Đường thẳng có vectơ chỉ phương
nên có hệ số góc
.
Vậy hệ số góc của đường thẳng là .
Gieo một đồng tiền liên tiếp 3 lần. Xác suất của biến cố ![]() : "kết quả của 3 lần gieo là như nhau" là bao nhiêu?
: "kết quả của 3 lần gieo là như nhau" là bao nhiêu?
Lần đầu có thể ra tùy ý nên xác suất là 1. Lần 2 và 3 phải giống lần 1 xác suất là .
Theo quy tắc nhân xác suất: .
Cho tập hợp ![]() có
có ![]() phần tử. Số tập con gồm
phần tử. Số tập con gồm ![]() phần tử của
phần tử của ![]() là:
là:
Số tập con gồm phần tử của
chính là số tổ hợp chập
của
phần tử, nghĩa là bằng
.
Phương trình có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?
Điều kiện: .
Ta có: .
Loại . Do đó phương trình có 1 nghiệm.
