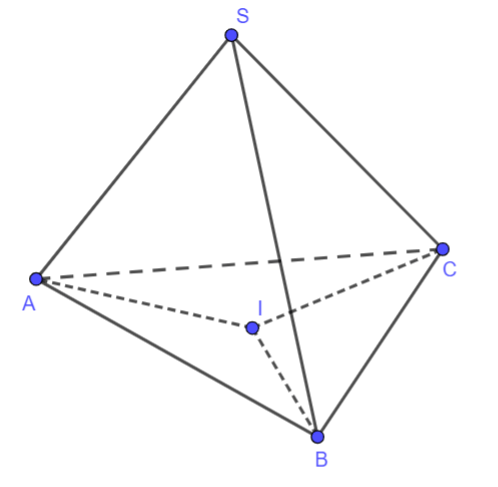
Cho hình chóp ![]() có đáy
có đáy ![]() là hình tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi
là hình tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi ![]() lần lượt là hình chiếu của điểm
lần lượt là hình chiếu của điểm ![]() trên cạnh
trên cạnh ![]() . Kết luận nào sau đây sai?
. Kết luận nào sau đây sai?
Hình vẽ minh họa
Ta có:
đúng
Ta có: đúng
Ta có: đúng
Vậy kết luận sai là: .