Lớp 11 Toán 11 - Kết nối tri thức với cuộc sống

Đề thi giữa HK2 Toán 11 Kết nối tri thức năm học 2023 – 2024 (Đề 4)

Mô tả thêm: Đề thi giữa HK2 Toán 11 được biên soạn chuẩn ma trận đề thi gồm 40 các câu hỏi trắc nghiệm bám sát chương trình sách Kết nối tri thức, giúp bạn học củng cố kiến thức chuẩn bị cho kì thi sắp tới
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Chọn mệnh đề đúng trong các mệnh đề sau?

    Ta có: \left\{ \begin{matrix} a\bot b \\ b//c \\ \end{matrix} ight.\ \Rightarrow a\bot c

    Vậy mệnh đề đúng là: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.”

  • Câu 2: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a; \widehat{ABC} = 60^{0}. Biết SO\bot(ABCD);SO = a\sqrt{3}. Gọi \alpha là góc giữa đường thẳng SB và mặt phẳng (SAC). Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Ta có:\left\{ \begin{matrix} BD\bot AC \\ BD\bot SO \\ \end{matrix} ight.\ \Rightarrow BD\bot(SAC)

    \Rightarrow (SBD)\bot(SAC)

    Mà (SBD) \cap (SAC) = SO

    \Rightarrow \left( SB;(SAC) ight) = (SB;SO) = \widehat{BSO}

    Ta có: \tan\widehat{BSO} = \frac{SB}{SO} = \frac{\frac{a\sqrt{3}}{2}}{a\sqrt{3}} = \frac{1}{2}

    \Rightarrow \widehat{BSO} = \arctan\frac{1}{2} = \alpha

    Vậy \alpha \in \left( 25^{0};27^{0} ight)

  • Câu 3: Thông hiểu

    Cho đồ thị hàm số y = f(x) như hình vẽ:

    Hàm số y = f(x) có thể là hàm số nào dưới đây?

    Dựa vào đồ thị ta có hàm số có tập xác định D\mathbb{= R} và hàm số nghịch biến suy ra hàm số tương ứng là y = \left(\frac{4}{5} ight)^{x}.

  • Câu 4: Thông hiểu

    Tính giá trị K = xy + z biết \log_{15}30 = \dfrac{1 +x\log2}{y\log3 + z\log5};\left( x,y,z\in\mathbb{ Z} ight)?

    Ta có:

    \log_{15}30 = \dfrac{1 + x\log2}{y\log3 +z\log5}

    Mặt khác

    \log_{15}30 =\frac{\log30}{\log15}

    = \frac{\log10 + \log3}{\log3 + \log5} =\frac{1 + \log3}{\log3 + \log5}

    \Rightarrow x = 1;y = 1;z = 1 \Rightarrow K = 2

  • Câu 5: Thông hiểu

    Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC). Tam giác ABC là:

    Giả sử tam giác ABC vuông tại A

    Khi đó B có hai đường thẳng BO và BA cùng vuông góc với mặt phẳng (OCA) 

    Điều này vô lí, do đó tam giác ABC không thể là tam giác vuông

    Từ O hạ OH \perp AB => CH \perp AB (theo định lí ba đường vuông góc)

    Vì điểm H giữa hai điểm A và B nên tam giác ABC không thể có góc tù.

    Suy ra ABC có ba góc nhọn.

  • Câu 6: Nhận biết

    Xác định nghiệm của bất phương trình \left( \frac{1}{7} ight)^{x^{2} + x} > \frac{1}{49}?

    Ta có:

    \left( \frac{1}{7} ight)^{x^{2} + x} > \frac{1}{49} \Leftrightarrow \left( \frac{1}{7} ight)^{x^{2} + x} > \left( \frac{1}{7} ight)^{2}

    \Leftrightarrow x^{2} + x < 2 \Leftrightarrow x^{2} + x - 2 < 0

    \Leftrightarrow - 2 < x < 1

    Vậy tập nghiệm của bất phương trình là x \in ( - 2;1)

  • Câu 7: Thông hiểu

    Cho số thực dương a tùy ý. Viết biểu thức M = a\sqrt{a^{3}\sqrt{a\sqrt{a}}} dưới dạng a^{\frac{x}{y}} trong đó \frac{x}{y} là phân số tối giản, x,y \in \mathbb{N}^{*}. Tính giá trị biểu thức H = x^{2} + y^{2}?

    Ta có:

    M = a\sqrt{a^{3}\sqrt{a\sqrt{a}}} = a\sqrt{a^{3}\sqrt{a.a^{\frac{1}{2}}}} = a\sqrt{a^{3}\sqrt{a^{\frac{3}{2}}}}

    = a\sqrt{a^{3}.a^{\frac{3}{4}}} = a.a^{\frac{15}{8}} = a^{\frac{23}{8}}

    \Rightarrow \frac{x}{y} = \frac{23}{8} \Rightarrow H = x^{2} + y^{2} = 593

  • Câu 8: Nhận biết

    Với m > 0;m eq 1 thì giá trị của \log_{\sqrt[3]{m}}m bằng bao nhiêu?

    Ta có: \log_{\sqrt[3]{m}}m =\log_{m^{\frac{1}{3}}}m = 3\log_{m}m = 3

  • Câu 9: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA = 3a\sqrt{2};SA\bot(ABCD). Tính \tan\left( SC;(SAD) ight)?

    Hình vẽ minh họa

    Ta có: ABCD là hình vuông \Rightarrow AC\bot BD

    Mặt khác SA\bot(ABCD) \Rightarrow SA\bot CD

    Suy ra CD\bot(SAD)

    => SD là hình chiếu của SC lên mặt phẳng (SAD)

    Do đó \left( SC;(SAD) ight) = (SC;SD) = \widehat{CSD}

    Xét tam giác SCD vuông tại D ta có:

    \tan\widehat{CSD} = \frac{CD}{SD} = \frac{CD}{\sqrt{SA^{2} + AD^{2}}} = \frac{a^{2}}{\sqrt{\left( 3a\sqrt{2} ight)^{2} + a^{2}}} = \frac{1}{\sqrt{19}} = \frac{\sqrt{19}}{19}

  • Câu 10: Thông hiểu

    Trên giá sách có 3 quyển sách giáo khoa và 4 quyển sách tham khảo. Gọi B là biến cố “Hai quyển sách cùng loại nằm cạnh nhau”. Tính số phần tử của biến cố B?

    Ta có: n(\Omega) = 7! = 5040

    Biến cố B là hai quyển sách cùng loại nằm cạnh nhau

    \Rightarrow \overline{B} là biến cố các quyển sách không cùng loại nằm cạnh nhau.

    Do số sách tham khảo có số lượng nhiều hơn sách giáo khoa nên để các quyển sách cùng loại không nằm cạnh nhau thì ta cần sắp xếp sách tham khảo ở các vị trí 1; 3; 5; 7 và các quyển sách kháo khoa nằm ở vị trí 2; 4; 6.

    \Rightarrow n\left( \overline{B} ight) = 3!.4! = 144

    \Rightarrow n(B) = n(\Omega) - n\left( \overline{B} ight) = 5040 - 144 = 4896

  • Câu 11: Thông hiểu

    Cho phương trình 2^{x^{2} - 3x + 2} + 2^{x^{2} + 6x + 5} = 2^{2x^{2} + 3x + 7} + 1. Tính tổng giá trị các nghiệm phương trình đã cho.

    Ta có:

    2^{x^{2} - 3x + 2} + 2^{x^{2} + 6x + 5} = 2^{2x^{2} + 3x + 7} + 1

    \Leftrightarrow 2^{x^{2} - 3x + 2} + 2^{x^{2} + 6x + 5} = 2^{x^{2} - 3x + 2}.2^{x^{2} + 6x + 5} + 1

    \Leftrightarrow \left( 2^{x^{2} - 3x + 2} - 1 ight) - 2^{x^{2} + 6x + 5}.\left( 2^{x^{2} - 3x + 2} - 1 ight) = 0

    \Leftrightarrow \left( 2^{x^{2} + 6x + 5} - 1 ight).\left( 2^{x^{2} - 3x + 2} - 1 ight) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} 2^{x^{2} + 6x + 5} - 1 = 0 \\ 2^{x^{2} - 3x + 2} - 1 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} 2^{x^{2} + 6x + 5} = 1 \\ 2^{x^{2} - 3x + 2} = 1 \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} x^{2} + 6x + 5 = 0 \\ x^{2} - 3x + 2 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = - 5 \\ x = 1 \\ x = 2 \\ \end{matrix} ight.

    Vậy tổng tất cả các nghiệm của phương trình là S = 1 + 2 + ( - 1) + ( - 5) = - 3

  • Câu 12: Nhận biết

    Tính giá trị biểu thức A = \sqrt[5]{- 4}.\sqrt[5]{8}.

    Ta có:

    A = \sqrt[5]{- 4}.\sqrt[5]{8} = \sqrt[5]{- 4.8} = \sqrt[5]{- 32} = - 2

  • Câu 13: Thông hiểu

    Cho hình lập phương ABCD.A_{1}B_{1}C_{1}D_{1}. Tính \left( AC;DA_{1} ight)?

    Hình vẽ minh họa

    Ta có:

    AC//A_{1}C_{1} \Rightarrow \left( AC;DA_{1} ight) = \left( A_{1}C_{1};DA_{1} ight) = \widehat{DA_{1}C_{1}}

    Do A_{1}C_{1};DA_{1};DC_{1} là các đường chéo hình vuông bằng nhau.

    Vậy tam giác AD_{1}C_{1} là tam giác đều \Rightarrow \widehat{DA_{1}C_{1}} = 60^{0}

    \Rightarrow \left( AC;DA_{1} ight) = \widehat{DA_{1}C_{1}} = 60^{0}

  • Câu 14: Nhận biết

    Với a,b \in \mathbb{R}^{+} thỏa mãn biểu thức 3\log a + 2\log b = 1. Khẳng định nào dưới đây đúng?

    Ta có:

    3\log a + 2\log b = 1 \Leftrightarrow \log a^{3} + \log b^{2} = 1

    \Leftrightarrow \log\left( a^{3}b^{2} ight) = 1 \Leftrightarrow a^{3}b^{2} = 10

  • Câu 15: Thông hiểu

    Quan sát đồ thị hàm số sau:

    Chọn khẳng định đúng?

    Quan sát đồ thị ta thấy

    Hai hàm số y = n^{x};y = t^{x} đồng biến nên n,t > 1

    Hàm số y = m^{x} nghịch biến nên 0 < m < 1

    Vậy \left\{ \begin{matrix} 0 < m < 1 \\ n,t > 1 \\ \end{matrix} ight.

    Đường thẳng x = 1 cắt hai đồ thị hàm số y = n^{x};y = t^{x} lần lượt tại n,t và ta thấy n > t

    Vậy m < t < n

  • Câu 16: Thông hiểu

    Cho hình lập phương ABCD.A'B'C'D'. Đường thẳng nào dưới đây vuông góc với mặt phẳng (A'BD)?

    Hình vẽ minh họa

    Ta có: AB = AD = AA' = a nên A cách đều các điểm B,D,A'

    BC' = DC' = C'A' = a\sqrt{2} nên C' cách đều các điểm B,D,A'

    Do đó A; C’ cùng nằm trên đường tròn ngoại tiếp tam giác A'BD

    \Rightarrow AC'\bot(A'BD)

  • Câu 17: Thông hiểu

    Biết x,y là các số thực dương khác 1 thỏa mãn \log_{x}y = 2. Biến đổi biểu thức C = \log_{\frac{\sqrt{x}}{y}}\left(x\sqrt[3]{y} ight) ta được kết quả là:

    Ta có:

    C = \log_{\frac{\sqrt{x}}{y}}\left(x\sqrt[3]{y} ight) = \frac{\log_{x}\left( x\sqrt[3]{y}ight)}{\log_{x}\left( \dfrac{\sqrt{x}}{y} ight)}

    = \dfrac{\log_{x}x +\log_{x}y^{\frac{1}{3}}}{\dfrac{1}{2}\log_{x}x - \log_{x}y}

    = \dfrac{1 +\dfrac{1}{3}\log_{x}y}{\dfrac{1}{2} - \log_{x}y} = \dfrac{1 +\dfrac{1}{3}.2}{\dfrac{1}{2} - 2} = - \dfrac{10}{9}

  • Câu 18: Nhận biết

    Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng (ABC). Gọi H là hình chiếu vuông góc của S lên cạnh BC. Tìm khẳng định đúng dưới đây?

    Hình vẽ minh họa

    Ta có: SA\bot(ABC) \Rightarrow SA\botBC

    Mà SH\bot BC

    \Rightarrow BC\bot(SAH) \RightarrowBC\bot AH

  • Câu 19: Nhận biết

    Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng?

    Mệnh đề đúng: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia”.

  • Câu 20: Vận dụng

    Cho hàm số y = f(x) = \frac{2016^{x}}{2016^{x} + \sqrt{2016}}. Tính giá trị của biểu thức:

    S = f\left( \frac{1}{2017} ight) + f\left( \frac{2}{2017} ight) + ... + f\left( \frac{2016}{2017} ight)

    Vì f(1 - x) = \frac{\sqrt{2016}}{2016^{x} + \sqrt{2016}} nên f(x) + f(1 - x) = 1

    \Rightarrow S = f\left( \frac{1}{2017} ight) + f\left( \frac{2}{2017} ight) + ... + f\left( \frac{2016}{2017} ight)

    \Rightarrow S = \left\lbrack f\left( \frac{1}{2017} ight) + f\left( \frac{2016}{2017} ight) ightbrack + \left\lbrack f\left( \frac{2}{2017} ight) + f\left( \frac{2015}{2017} ight) ightbrack

    + ... + \left\lbrack f\left( \frac{1008}{2017} ight) + f\left( \frac{1009}{2017} ight) ightbrack

    = 1008

  • Câu 21: Nhận biết

    Gieo ngẫu nhiên một đồng xu cân đối và đồng chất 5 lần. Không gian mẫu của phép thử có bao nhiêu phần tử?

    Mỗi lần gieo đồng xu có hai khả năng xảy ra nên khi tung đồng xu đó 5 lần thì theo quy tắc nhân ta có: {2^5} = 32

    Vậy số phần tử của không gian mẫu là n\left( \Omega ight) = 32

  • Câu 22: Thông hiểu

    Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu vuông góc của điểm S trên mặt phẳng (ABC) là:

    Gọi I là hình chiếu vuông góc của S trên mặt phẳng (ABCD)

    M, N, P lần lượt là hình chiếu vuông góc của S trên các cạnh AB, AC, BC.

    Khi đó ta có: \left\{ \begin{matrix}SI\bot AB \\SM\bot AB \\\end{matrix} ight.\ \Rightarrow AB\bot(SIM) \Rightarrow AB\botIM

    Tương tự ta có: AC\bot IN,IP\botBC

    Khi đó \left( (SAB);(ABC) ight) =(SM,IM) = \widehat{SMI}

    Tương tự suy ra \widehat{SMI} =\widehat{SNI} = \widehat{SPI}

    => \Delta SMI = \Delta SNI = \DeltaSPI \Rightarrow IM = IN = IP

    => I là tâm đường tròn nội tiếp tam giác ABC.

  • Câu 23: Nhận biết

    Giá trị B = \sqrt[3]{2021}.\sqrt[5]{2021} viết dưới dạng lũy thừa với số mũ hữu tỉ là:

    Ta có:

    B = \sqrt[3]{2021}.\sqrt[5]{2021} = 2021^{\frac{1}{3}}.2021^{\frac{1}{5}} = 2021^{\frac{1}{3} + \frac{1}{5}} = 2021^{\frac{8}{15}}

  • Câu 24: Thông hiểu

    Tìm số nghiệm của phương trình \log_{3}(2a + 1) + \log_{3}(a - 3) = 2?

    Điều kiện xác định \left\{ \begin{matrix}2a + 1 > 0 \\a - 3 > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}a > - \dfrac{1}{2} \\a > 3 \\\end{matrix} ight.\ \Rightarrow a > 3

    Phương trình đã cho tương đương:

    \Leftrightarrow \log_{3}\left\lbrack (2a+ 1)(a - 3) ightbrack = \log_{3}9

    \Leftrightarrow (2a + 1)(a - 3) = 9

    \Leftrightarrow 2a^{2} - 5a - 12 = 0\Leftrightarrow \left\lbrack \begin{matrix}a = 4(tm) \\a = - \dfrac{3}{2}(ktm) \\\end{matrix} ight.

    Vậy phương trình có 1 nghiệm duy nhất.

  • Câu 25: Thông hiểu

    Với điều kiện a \in \mathbb{R}^{+}, đơn giản biểu thức G = \frac{a^{\frac{4}{3}}.\left( a^{- \frac{1}{3}} + a^{\frac{2}{3}} ight)}{a^{\frac{1}{4}}.\left( a^{\frac{3}{4}} + a^{- \frac{1}{4}} ight)} thu được kết quả là:

    Ta có:

    G = \frac{a^{\frac{4}{3}}.\left( a^{- \frac{1}{3}} + a^{\frac{2}{3}} ight)}{a^{\frac{1}{4}}.\left( a^{\frac{3}{4}} + a^{- \frac{1}{4}} ight)} = \frac{a^{\frac{4}{3}}.a^{- \frac{1}{3}} + a^{\frac{4}{3}}.a^{\frac{2}{3}}}{a^{\frac{1}{4}}.a^{\frac{3}{4}} + a^{\frac{1}{4}}.a^{- \frac{1}{4}}}

    = \frac{a + a^{2}}{a + 1} = \frac{a(a + 1)}{a - 1} = a

  • Câu 26: Vận dụng cao

    Một người gửi 150 triệu đồng vào ngân hàng theo hình thức lãi kép với lãi suất 0,8%/tháng. Kể từ ngày gửi nếu mỗi cuối tháng người đó rút đều đặn 3 triệu đồng (trừ tháng cuối) thì sau bao nhiêu tháng số tiền đó sẽ được tút hết? (Tháng cuối cùng là tháng mà số tiền còn trong ngân hàng không vượt quá 3 triệu đồng và khi đó người đó rút hết toàn bộ số tiền còn lại).

    Gọi A_{n} là số tiền còn lại sau khi người đó rút đến tháng thứ n, A là số tiền gửi vào, r là lãi suất hàng tháng và X là số tiền rút ra hàng tháng.

    Ta có:

    A_{1} = A(1 + r) - X

    A_{2} = A(1 + r)^{2} - X\left\lbrack (1 + r) + 1 ightbrack

    A_{3} = A(1 + r)^{3} - X\left\lbrack (1 + r)^{2} + (1 + r) + 1 ightbrack

    ….

    A_{n} = A(1 + r)^{n} - X\left\lbrack (1 + r)^{n - 1} + (1 + r)^{n - 2} + ... + (1 + r) + 1 ightbrack

    \Rightarrow A_{n} = A(1 + r)^{n} - X.\frac{(1 + r)^{n - 1} - 1}{r}

    \Rightarrow n = \log_{1 + r}\frac{A_{n}.r- X}{A.r - X}

    \Rightarrow n = log_{1 + 0,8\%}\frac{- 3.10^{6}}{150.10^{6}.0,8\% - 3.10^{6}} = 64,10827659

    Vậy n = 64 tháng.

  • Câu 27: Vận dụng

    Giáo viên chọn 16 học sinh gồm 4 học sinh giỏi, 5 học sinh khá và 7 học sinh trung bình để lập thành 4 nhóm thảo luận, mỗi nhóm có 4 học sinh. Hỏi có bao nhiêu kết quả thuận lợi cho biến cố N “Nhóm nào cũng có học sinh giỏi, học sinh khá”?

    n(N) = 21772800

    Đáp án là:

    Giáo viên chọn 16 học sinh gồm 4 học sinh giỏi, 5 học sinh khá và 7 học sinh trung bình để lập thành 4 nhóm thảo luận, mỗi nhóm có 4 học sinh. Hỏi có bao nhiêu kết quả thuận lợi cho biến cố N “Nhóm nào cũng có học sinh giỏi, học sinh khá”?

    n(N) = 21772800

    Đánh số thứ tự các nhóm là A, B, C, D

    Bước 1: xếp vào mỗi nhóm một học sinh giỏi có 4! Cách.

    Bước 2: xếp 5 học sinh khá vào 4 nhóm thì 1 nhóm có 2 học sinh khá và 3 nhóm có 1 học sinh khá.

    Chọn nhóm có 2 học sinh khá có 4 cách, chọn 2 học sinh khá có C_{5}^{2} cách, xếp 3 học sinh khá còn lại có 3! cách.

    Bước 3: xếp 7 học sinh trung bình

    + Nhóm có 2 học sinh khá cần xếp vào đó 1 học sinh trung bình, có 7 cách chọn học sinh.

    + Nhóm có 1 học sinh khá cần xếp vào đó 2 học sinh trung bình.

    Chọn nhóm 2 học sinh trung bình trong 6 học sinh và xếp vào 3 nhóm có C_{6}^{2}.3 cách.

    Chọn nhóm 2 học sinh trung bình trong nhóm học sinh và xếp vào 2 nhóm có C_{4}^{2}.2 cách.

    Xếp 2 học sinh trung bình còn lại có 1 cách.

    Do đó số cách sắp xếp là: 4!.4.C_{5}^{2}.3!.7.C_{6}^{2}.3.C_{4}^{2}..1 =21772800

    Vậy n(N) = 21772800

  • Câu 28: Nhận biết

    Biết a là số thực dương khác 1. Viết và thu gọn biểu thức a^{\frac{3}{2022}}.\sqrt[2022]{a} dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó?

    Ta có:

    a^{\frac{3}{2022}}.\sqrt[2022]{a} = a^{\frac{3}{2022}}.a^{\frac{1}{2022}} = a^{\frac{3}{2022} + \frac{1}{2022}} = a^{\frac{4}{2022}} = a^{\frac{2}{1011}}

  • Câu 29: Vận dụng

    Tìm cặp số (a;b). Biết \frac{1}{2019!}\left( 1 - \frac{1}{2} ight)^{1}.\left( 1 - \frac{1}{3} ight)^{2}.\left( 1 - \frac{1}{4} ight)^{3}...\left( 1 - \frac{1}{2019} ight)^{2018} = a^{b}.

    Ta có:

    \frac{1}{2019!}\left( 1 - \frac{1}{2} ight)^{1}.\left( 1 - \frac{1}{3} ight)^{2}.\left( 1 - \frac{1}{4} ight)^{3}...\left( 1 - \frac{1}{2019} ight)^{2018}

    = \frac{1}{2019!}\left( \frac{1}{2} ight)^{1}.\left( \frac{2}{3} ight)^{2}.\left( \frac{3}{4} ight)^{3}...\left( \frac{2018}{2019} ight)^{2018}

    = \frac{1}{2019!}.\frac{1.2.3...2018}{2019^{2018}}

    = \frac{1}{2019^{2019}} = 2019^{- 2019}

  • Câu 30: Thông hiểu

    Cho tứ diện đều ABCD cạnh bằng 1, M là trung điểm của BC. Khi đó \cos(AB;DM) là:

    Hình vẽ minh họa

    Gọi E là trung điểm cạnh AC. Khi đó ta có: EM // AB.

    \Rightarrow \cos(AB,DM) = \cos(EM;DM) = \widehat{DME}

    Ta có: ABCD là tứ diện đều cạnh bằng 1 và EA = EC;BM = MC

    \Rightarrow DM = \frac{\sqrt{3}}{2};DE = \frac{\sqrt{3}}{2};EM = \frac{AB}{2} = \frac{1}{2}

    \Rightarrow \cos\widehat{DME} = \frac{DM^{2} + ME^{2} - DE^{2}}{2.DM.EM} = \frac{1}{2\sqrt{3}} = \frac{\sqrt{3}}{6}

    \Rightarrow \cos(AB,DM) = \frac{\sqrt{3}}{6}

  • Câu 31: Nhận biết

    Hàm số nào trong các hàm số sau đây là hàm nghịch biến trên tập số thực?

    Hàm số y = (0,25)^{x} nghịch biến trên \mathbb{R} vì 0 < 0,25 < 1

  • Câu 32: Vận dụng

    Cho n là số nguyên dương và một số a bất kì với a > 0,a eq 1. Biết

    \log_{a}2019 + \log_{\sqrt{a}}2019 +\log_{\sqrt[3]{a}}2019 + ... + \log_{\sqrt[n]{a}}2019 =2033136\log_{a}2019

    Khi đó giá trị của n là bao nhiêu?

    Ta có:

    \log_{a}2019 + \log_{\sqrt{a}}2019 +\log_{\sqrt[3]{a}}2019 + ... + \log_{\sqrt[n]{a}}2019 =2033136\log_{a}2019

    \Leftrightarrow \log_{a}2019 +2\log_{a}2019 + 3\log_{a}2019 + ... + n\log_{a}2019 =2033136\log_{a}2019

    \Leftrightarrow (1 + 2 + 3 + ... +n)\log_{a}2019 = 2033136\log_{a}2019

    \Leftrightarrow 1 + 2 + 3 + ... + n = 2033136

    \Leftrightarrow \frac{n(n + 1)}{2} = 2033136

    \Leftrightarrow \left\lbrack \begin{matrix} n = 2016(tm) \\ n = - 2017(ktm) \\ \end{matrix} ight.

    Vậy n = 2016

  • Câu 33: Vận dụng

    Cho lăng trụ đều ABC.A’B’C’ có AB = 1; AA’ = m (m > 0). Để góc giữa AB’ và BC’ bằng 600 thì m có giá trị là bao nhiêu?

    Hình vẽ minh họa

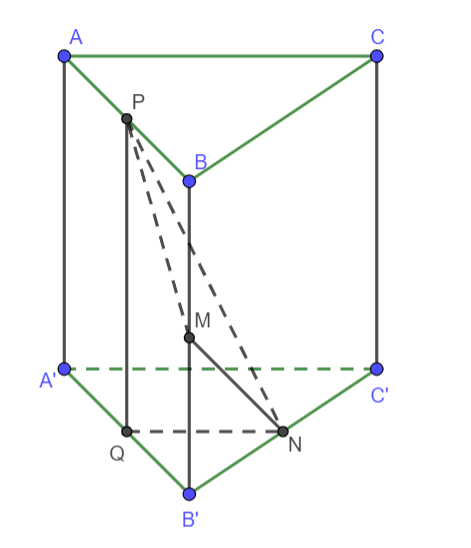
    Tìm giá trị của m để góc tạo bời 2 đường thẳng thỏa mãn điều kiện

    Giả sử M, N, O lần lượt là trung điểm của BB’; B’C’; AB

    => MP // AB’; MN // BC’

    => Góc cần tìm là góc giữa MP và MN

    => MP = MN = \frac{{\sqrt {{m^2} + 1} }}{2}

    Lấy Q là trung điểm của A’B’ khi đó suy ra:

    \begin{matrix} PN = \sqrt {P{Q^2} + Q{N^2}} = \sqrt {{m^2} + \dfrac{1}{4}} \hfill \\ \Rightarrow \cos \widehat {PMN} = \dfrac{{P{M^2} + M{N^2} - P{N^2}}}{{2.PM.MN}} = \pm \dfrac{1}{2} \hfill \\ \Rightarrow m = \sqrt 2 \hfill \\ \end{matrix}

  • Câu 34: Nhận biết

    Tìm nghiệm phương trình \log_{2}(2x - 3) = \log_{2}(x + 1)?

    Điều kiện x > \frac{3}{2}

    Ta có:

    \log_{2}(2x - 3) = \log_{2}(x + 1)

    \Leftrightarrow 2x - 3 = x + 1 \Leftrightarrow x = 4(tm)

    Vậy phương trình có nghiệm x = 4.

  • Câu 35: Thông hiểu

    Một hộp chứa 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau và 5 viên bi xanh khác nhau. Gọi A là biến cố “Sắp xếp các viên bi thành một dãy sao cho các viên bi cùng màu nằm cạnh nhau”. Các kết quả thuận lợi của biến cố A là:

    Ta có:

    Số cách sắp xếp 3 viên bi đen thành một dãy bằng 3!

    Số cách sắp xếp 3 viên bi đỏ thành một dãy bằng 4!

    Số cách sắp xếp 3 viên bi xanh thành một dãy bằng 5!

    Số cách sắp xếp 3 viên bi nhóm thành một dãy bằng 3!

    Vậy số phần tử của tập hợp A là: n(A) = 3!.4!.5!.3! = 103680

  • Câu 36: Nhận biết

    Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng nhau và bằng a. Số đo góc giữa hai đường thẳng SA và CD bằng bao nhiêu?

    Hình vẽ minh họa

    Ta có: AB//CD \Rightarrow (SA;CD) = (SA;AB) = \widehat{SAB}

    Tam giác SAB đều nên \widehat{SAB} = 60^{0}

    \Rightarrow (SA;CD) = \widehat{SAB} = 60^{0}

  • Câu 37: Nhận biết

    Tìm điều kiện xác định của hàm số y = f(x) = \frac{1}{\log_{2}x - 1}?

    Điều kiện xác định của hàm số y = f(x) = \frac{1}{\log_{2}x - 1} là:

    \left\{ \begin{matrix}x > 0 \\ \log_{2}x - 1 eq 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x > 0 \\ \log_{2}x eq 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x > 0 \\x eq 2 \\\end{matrix} ight.

    Vậy tập xác định của hàm số đã cho là D = (0; + \infty)\backslash\left\{ 2 ight\}.

  • Câu 38: Nhận biết

    Cho (P) và (Q) là hai mặt phẳng vuông góc với nhau và giao tuyến của chúng là đường thẳng m. Gọi a, b, c, d là các đường thẳng. Xét các mệnh đề sau:

    (1) Nếu a ⊂ (P) và a ⊥ m thì a ⊥ (Q).

    (2) Nếu b ⊥ m thì b ⊂ (P) hoặc b ⊂ (Q).

    (3) Nếu c // m thì c // (P) hoặc c // (Q).

    (4) Nếu d ⊥ m thì d ⊥ (P).

    Có bao nhiêu mệnh đề đúng trong các mệnh đề đã cho?

    (1) Nếu a ⊂ (P) và a ⊥ m thì a ⊥ (Q). ---> đúng

    (2) Nếu b ⊥ m thì b ⊂ (P) hoặc b ⊂ (Q). ---> sai

    (3) Nếu c // m thì c // (P) hoặc c // (Q). ---> đúng

    (4) Nếu d ⊥ m thì d ⊥ (P). ---> sai

  • Câu 39: Nhận biết

    Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi X là biến cố “Ba lần liên tiếp kết quả như nhau” và Y là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp”. Chọn khẳng định đúng?

    Ta có:

    X = \left\{ SSS;NNN ight\}

    Y = \left\{ SSS;SSN;NNN ight\}

    \Rightarrow X \cup Y = \left\{ SSS;SSN;NSS;NNN ight\}

  • Câu 40: Vận dụng cao

    Trong không gian cho tam giác ABC. Xác định vị trí của điểm M sao cho giá trị của biểu thức P = MA2 + MB2 + MC2 đạt giá trị nhỏ nhất

    Gọi G là trọng tâm giác ABC => \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}

    Ta có:

    \begin{matrix}P = \left( \overrightarrow{MG} + \overrightarrow{GA} ight)^{2} +\left( \overrightarrow{MG} + \overrightarrow{GB} ight)^{2} + \left(\overrightarrow{MG} + \overrightarrow{GC} ight)^{2}\hfill \\= 3MG^{2} + 2\overrightarrow{MG}.\left( \overrightarrow{GA} +\overrightarrow{GB} + \overrightarrow{GC} ight) + GA^{2} + GB^{2} +GC^{2}\hfill \\= 3MG^{2} + GA^{2} + GB^{2} + GC^{2} \hfill \\\geq GA^{2} + GB^{2} + GC^{2}\hfill \\\end{matrix}

    Dấu bằng xảy ra khi M trùng với G

    Vậy P_{\min} = GA^{2} + GB^{2} + GC^{2} với M trùng G là trọng tâm tam giác ABC

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi giữa HK2 Toán 11 Kết nối tri thức năm học 2023 – 2024 (Đề 4) Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 1 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi giữa HK2 Toán 11 Kết nối tri thức năm học 2023 – 2024 (Đề 4)
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập