Cho hai đường thẳng ![]() và
và ![]() . Tính góc hợp bởi hai đường thẳng đã cho?
. Tính góc hợp bởi hai đường thẳng đã cho?
Ta có:
Vectơ pháp tuyến của đường thẳng là:
Vectơ pháp tuyến của đường thẳng là:
Ta có:
Vậy góc hợp bởi hai đường thẳng bằng .
Cho hai đường thẳng ![]() và
và ![]() . Tính góc hợp bởi hai đường thẳng đã cho?
. Tính góc hợp bởi hai đường thẳng đã cho?
Ta có:
Vectơ pháp tuyến của đường thẳng là:
Vectơ pháp tuyến của đường thẳng là:
Ta có:
Vậy góc hợp bởi hai đường thẳng bằng .
Trục đối xứng của parabol y = − x2 + 5x + 3 là đường thẳng có phương trình
Trục đối xứng của parabol y = ax2 + bx + c là đường thẳng .
Trục đối xứng của parabol y = − x2 + 5x + 3 là đường thẳng .
Lớp 11A có 20 học sinh nam và 15 học sinh nữ. Giáo viên chủ nhiệm muốn chọn một nhóm học sinh đại diện gồm 3 học sinh nam và 2 học sinh nữ. Hỏi có bao nhiêu cách chọn nhóm học sinh đại diện?
Số cách chọn 3 học sinh nam là cách.
Số cách chọn 2 học sinh nữ là: cách.
Vậy số cách chọn nhóm học sinh đại diện là: cách.
Trong mặt phẳng tọa độ ![]() , cho tọa độ các điểm
, cho tọa độ các điểm ![]() . Điểm
. Điểm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() có phương trình
có phương trình ![]() sao cho
sao cho ![]() đạt giá trị nhỏ nhất. Kết quả nào dưới đây chính xác?
đạt giá trị nhỏ nhất. Kết quả nào dưới đây chính xác?
Gọi G là trọng tâm tam giác ABC suy ra G(0; 1)
Ta có:
(theo tính chất)
Khi đó để biểu thức đạt giá trị nhỏ nhất thì M là hình chiếu vuông góc của G trên đường thẳng
Vì mà VTCP của đường thẳng d là:
Khi đó ta có:
.
Biết phương trình ![]() có một nghiệm có dạng
có một nghiệm có dạng ![]() , trong đó a, b, c là các số nguyên tố. Tính S = a + b + c.
, trong đó a, b, c là các số nguyên tố. Tính S = a + b + c.
Điều kiện:
Với điều kiện trên, phương trình tương đương
⇔ x2 − 3x + 1 = 0
hoặc
Theo yêu cầu đề bài ta chọn nghiệm .
Vậy a = 3, b = 5, c = 2 nên S = a + b + c = 10.
Một hộp chứa 5 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên 1 viên bi trong hộp. Số khả năng xảy ra là:
Áp dụng quy tắc cộng ta có số khả năng xảy ra là: 5 + 4 = 9 khả năng.
Cho hàm số: ![]() . Tìm x để
. Tìm x để ![]()
Ta có:
Vậy x = 3 hoặc x = 0
Tổng các nghiệm của phương trình ![]() ?
?
Đặt . Khi đó phương trình đã cho trở thành:
Vì t ≥ 0 ⇒ t = 6, thay vào ta có .
x2 + 11 = 36 ⇔ x = ± 5.
Vậy phương trình có nghiệm là x = ± 5.
Tổng các nghiệm của phương trình là 0.
Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có đỉnh ![]()
Vì (P) có đỉnh nên ta có
. Vậy (P) : y = 3x2 + 3x − 2.
Trong mặt phẳng với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() và đường thẳng
và đường thẳng ![]() . Tìm tọa độ giao điểm của đường thẳng
. Tìm tọa độ giao điểm của đường thẳng ![]() và
và ![]() .
.
Gọi S là tập nghiệm của bất phương trình ![]() . Trong các tập hợp sau, tập nào không là tập con của S?
. Trong các tập hợp sau, tập nào không là tập con của S?
Tam thức bậc hai có hai nghiệm phân biệt là:
Vì a = 1 > 0 nên khi
.
Tập không phải tập con của S là:
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
Có 5 học sinh nam và 3 học sinh nữ xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp để 2 học sinh nam xen giữa 3 học sinh nữ? (Biết rằng cứ đổi 2 học sinh bất kì được cách mới)
Xếp cố định 3 học sinh nữ vào hàng trước, có 3! cách xếp. Chọn 2 học sinh nam bất kì cho vào 2 khoảng trống nằm giữa 2 học sinh nữ, số cách chọn là . Xem nhóm 5 học sinh này là 1 học sinh, lúc này còn 3 học sinh nam vậy là ta đang có 4 học sinh. Số cách xếp 4 học sinh này thành hàng dọc là 4!. Vậy số cách xếp cần tìm là.
.
Trong mặt phẳng với hệ tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]() ,
, ![]() và
và ![]() Trung tuyến
Trung tuyến ![]() của tam giác đi qua điểm
của tam giác đi qua điểm ![]() có hoành độ bằng
có hoành độ bằng ![]() thì tung độ của điểm
thì tung độ của điểm ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
Chọn
Cho hàm số ![]() . Rút gọn biểu thức
. Rút gọn biểu thức ![]() ta được:
ta được:
Ta có:
Suy ra:
Hệ số góc của đồ thị hàm số y = 2018x − 2019 bằng
Hệ số góc a = 2018.
Trong mặt phẳng tọa độ ![]() ,cho tam giác
,cho tam giác ![]() có tọa độ các điểm
có tọa độ các điểm ![]() . Đường thẳng
. Đường thẳng ![]() đi qua
đi qua ![]() và song song với
và song song với ![]() có phương trình tổng quát là:
có phương trình tổng quát là:
Ta có:
Phương trình tổng quát AC là:
Đường thẳng song song với
nên d có dạng
Do điểm
Vậy .
Giá trị của n bằng bao nhiêu, biết ![]()
Điều kiện: .
Thay vào phương trình, ta được
(đúng). Do đó
là nghiệm của phương trình.
Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
Điều kiện:
Số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A là tổ hợp chập 3 của n phần tử
=> Số tam giác là: (tam giác)
Số đoạn thẳng được nối từ 2 điểm thuộc A là tổ hợp chập n phần tử
=> Số đoạn thẳng là:
Theo bài ra ta có:
Số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
Vậy n = 8.
Trong hệ trục tọa độ ![]() , viết phương trình đường trung trực của đoạn thẳng
, viết phương trình đường trung trực của đoạn thẳng ![]() biết
biết ![]() ?
?
Đường thẳng trung trực của là đường thẳng đi qua trung điểm
của
và nhận
làm vectơ pháp tuyến. Khi đó:
Vậy phương trình đường trung trực của MN là .
Công thức nào dưới đây là công thức tính khoảng cách từ một điểm ![]() đến đường thẳng
đến đường thẳng ![]() ?
?
Công thức tính khoảng cách từ một điểm đến đường thẳng
là:
Đếm số cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài. Biết các sách Văn phải xếp kề nhau?
Vì các sách Văn phải xếp kề nhau nên ta xem cuốn sách Văn là một phần tử.
Xếp cuốn sách toán lên kệ có
cách.
Giữa cuốn sách Toán có 8 khoảng trống, ta xếp phần tử chứa
cuốn sách Văn vào
vị trí đó có
cách.
cuốn sách Văn có thể hoán đổi vị trí cho nhau ta được
cách.
Vậy số cách sắp xếp thỏa mãn yêu cầu bài toán là. .
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Hệ số góc
. Hệ số góc ![]() của đường thẳng
của đường thẳng ![]() là:
là:
Ta có:
Đường thẳng có vectơ chỉ phương
nên có hệ số góc
.
Vậy hệ số góc của đường thẳng là .
Cho hai đường thẳng ![]() và
và ![]() với
với ![]() . Nếu
. Nếu ![]() vô nghiệm thì vị trí tương đối của hai đường thẳng là:
vô nghiệm thì vị trí tương đối của hai đường thẳng là:
Số giao điểm của hai đường thẳng đã cho là nghiệm của hệ phương trình .
Nếu hệ phương trình trên vô nghiệm thì hai đường thẳng không có điểm chung, nghĩa là hai đường thẳng song song với nhau.
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Hãy chỉ ra một vectơ pháp tuyến của đường thẳng
. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ![]() ?
?
Ta có: Vectơ pháp tuyến của đường thẳng là:
.
Tập nghiệm của bất phương trình ![]() là
là
Ta có: .
Tìm tập xác định của hàm số ![]() .
.
Điều kiện xác định: 4x2 − 4x + 1 ≥ 0 ⇔ (2x−1)2 ≥ 0 (luôn đúng với mọi x ∈ ℝ).
Do đó tập xác định D = ℝ.
Tính tổng các chữ số gồm 5 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5?
Có 120 số có 5 chữ số được lập từ 5 chữ số đã cho.
Bây giờ ta xét vị trí của một chữ số trong 5 số 1, 2, 3, 4, 5 chẳng hạn ta xét số 1. Số 1 có thể xếp ở 5 vị trí khác nhau, mỗi vị trí có 4!=24 số nên khi ta nhóm các các vị trí này lại có tổng là : .
Vậy tổng các số có 5 chữ số là : .
Trong các hàm số sau, hàm số nào là hàm số đồng biến trên khoảng ![]() ?
?
Hàm số là hàm số bậc nhất có hệ số a = 1 > 0 nên hàm số
đồng biến trên tập số thực.
Vậy hàm số đồng biến trên khoảng
.
Từ tập hợp các chữ số ![]() có thể lập được bao nhiêu số lẻ có bốn chữ số khác nhau?
có thể lập được bao nhiêu số lẻ có bốn chữ số khác nhau?
Gọi số tự nhiên có bốn chữ số cần tìm có dạng
Ta có: là số lẻ nên
là số lẻ. => Số cách chọn d có 3 cách.
Tiếp theo chọn a có 5 cách chọn
Sau đó chọn b có 4 cách chọn
Cuối cùng chọn c có 3 cách chọn
Vậy có thể lập được (số) thỏa mãn yêu cầu đề bài.
Cho tam thức bậc hai ![]() . Tìm tất cả các giá trị thực của tham số m để bất phương trình
. Tìm tất cả các giá trị thực của tham số m để bất phương trình ![]() vô nghiệm?
vô nghiệm?
Bất phương trình: vô nghiệm khi và chỉ khi
Xét
Với thì (*)
loại giá trị
.
Với thì bất phương trình (*)
bất phương trình vô nghiệm, nhận giá trị
.
Xét
Vậy thì bất phương trình (*) vô nghiệm.
Tìm tất cả các giá trị của m để bất phương trình ![]() với mọi x ∈ ℝ
với mọi x ∈ ℝ
Để bất phương trình với mọi x ∈ ℝ thì:
Tam thức bậc hai ![]() :
:
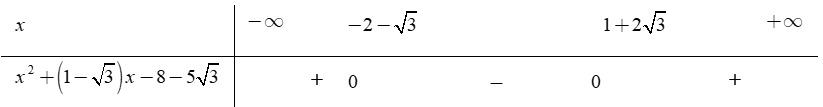
Dựa vào bảng xét dấu, chọn đáp án Âm với mọi .
Tất cả các giá trị của tham số m để phương trình ![]() có nghiệm là:
có nghiệm là:
ĐKXĐ x > − 1
pt ⇔ 3mx + 1 + x + 1 = 2x + 5m + 3 ⇔ (3m−1)x = 5m + 1.
Phương trình đã cho có nghiệm .
Tính số cách sắp xếp 8 học sinh thành 1 hàng dọc?
Số cách sắp xếp 8 học sinh thành 1 hàng dọc là 8! = 40320 cách.
Có bao nhiêu số tự nhiên có ba chữ số dạng ![]() với
với ![]() ,
, ![]() ,
, ![]() sao cho
sao cho ![]() .
.
Vì số tự nhiên có ba chữ số dạng với
,
,
sao cho
nên
,
,
. Suy ra số các số có dạng
là
.
Trong mặt phẳng ![]() , cho điểm
, cho điểm ![]() và đường thẳng
và đường thẳng ![]() . Khoảng cách từ điểm
. Khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() bằng:
bằng:
Khoảng cách từ điểm P đến đường thẳng (d) là:
.
Trong mặt phẳng với hệ tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]() và
và ![]() song song nhau. Đường thẳng vừa song song và cách đều với
song song nhau. Đường thẳng vừa song song và cách đều với ![]() là:
là:
Phương trình sau có bao nhiêu nghiệm ![]() ?
?
Điều kiện xác định: .
Với thay vào phương trình thỏa mãn. Vậy phương trình có một nghiệm.
Trong mặt phẳng ![]() có đường thẳng
có đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và tạo với đường thẳng
và tạo với đường thẳng ![]() một góc bằng
một góc bằng ![]() . Biết rằng
. Biết rằng ![]() có dạng
có dạng ![]() và
và ![]() . Tính tổng hai giá trị
. Tính tổng hai giá trị ![]() và
và ![]() ?
?
Gọi là vectơ pháp tuyến của đường thẳng
.
Phương trình tổng quát của đường thẳng là:
Ta có:
Vậy ta có phương trình của là:
và
Vậy
