Trong mặt phẳng tọa độ ![]() , cho hình chữ nhật
, cho hình chữ nhật ![]() có điểm
có điểm ![]() . Gọi
. Gọi ![]() đối xứng với điểm
đối xứng với điểm ![]() qua
qua ![]() , điểm
, điểm ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() lên đường thẳng
lên đường thẳng ![]() . Biết rằng tọa độ điểm
. Biết rằng tọa độ điểm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() . Khi đó:
. Khi đó:
Ta có: ADB’C là hình bình hành
Mà
Tam giác vuông cân tại I
là hình thang cân =>
đi qua điểm
và có vecto pháp tuyến
Phương trình CI:









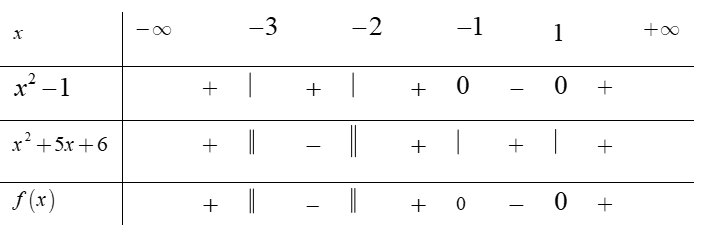
 là?
là?