Cho số phức ![]() . Số phức
. Số phức ![]() bằng:
bằng:
Ta có:
Cho số phức ![]() . Số phức
. Số phức ![]() bằng:
bằng:
Ta có:
Tính góc của hai đường thẳng ![]() và
và ![]() .
.
Theo đề bài, ta có (d’) và (d) có vec-tơ chỉ phương lần lượt là:
Áp dụng công thức cosin của góc giữa 2 đường thẳng, ta có:
Trong không gian với hệ tọa độ ![]() cho điểm
cho điểm ![]() và mặt phẳng
và mặt phẳng ![]() , m là tham số. Gọi là hình chiếu vuông góc của điểm trên . Tính khi khoảng cách từ điểm đến lớn nhất ?
, m là tham số. Gọi là hình chiếu vuông góc của điểm trên . Tính khi khoảng cách từ điểm đến lớn nhất ?
Ta có
Xét hàm số
Ta lập bảng biến thiên cho hàm số trên, được:
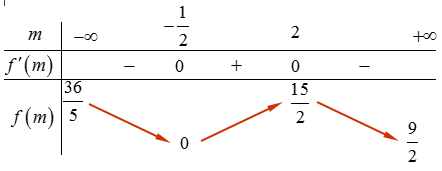
Qua bảng biến thiên, ta thấy hàm số đạt GTLN khi
Đường thẳng qua A và vuông góc với (P) có phương trình là
Ta có
Hàm số ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên
trên ![]() thỏa mãn
thỏa mãn ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có:
Lại có
Do đó
Vậy .
Tìm số phức ![]() trong phương trình sau:
trong phương trình sau: ![]()
Ta có
Cho a, b là các số hữu tỉ thỏa mãn
![]()
Tính giá trị biểu thức M = a + b.
=>
=>
Cho hai số phức ![]() . Môđun của số phức
. Môđun của số phức ![]() là:
là:
Ta có:
Cho hai đường thẳng trong không gian Oxyz: ![]() ,
, ![]() . Với
. Với ![]() . Gọi
. Gọi ![]() và
và ![]() . (D) và (d) song song khi và chỉ khi:
. (D) và (d) song song khi và chỉ khi:
Để xét điều kiện (D) và (d) cắt nhau ta cẩn kiểm tra rằnng (D) và d cùng nằm trong 1 mặt phẳng hay ta có:
và (d) cùng nằm trong một mặt phẳng
Để (D) và d song song, ta sẽ xét tỉ số chứng minh chúng cùng phương rồi kiểm tra rằng d không nằm trong (D):
và (d) cùng phương
và
và (d) song song.
Một ô tô đang chuyển động đều với vận tốc ![]() thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc
thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc ![]() (trong đó
(trong đó ![]() là thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian
là thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian ![]() giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu?
giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu?
Khi dừng hẳn
Khi đó trong 8s trước khi dừng hẳn vật di chuyển được (bao gồm 2s trước khi đạp phanh):
Diện tích hình phẳng giới hạn bởi các đường ![]() , trục hoành,
, trục hoành, ![]() và
và ![]() bằng
bằng
Hình vẽ minh họa
Phương trình hoành độ giao điểm
Diện tích hình giới hạn là
Tính ![]() ?
?
Áp dụng công thức
Suy ra
Trong các khẳng định sau, khẳng định nào sai?
Ta có:
Vậy khẳng định sai là: .
Cho 3 mặt phẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() chứa giao tuyến của
chứa giao tuyến của ![]() ,vuông góc với
,vuông góc với ![]() có phương trình tổng quát:
có phương trình tổng quát:
Mặt phẳng thuộc chùm mặt phẳng
nên phương trình có dạng:
Vì vuông góc với
nên ta được:
Vậy ta có phương trình là :
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Phương trình mặt phẳng
. Phương trình mặt phẳng ![]() cắt trục
cắt trục ![]() lần lượt tại
lần lượt tại ![]() (không trùng với gốc tọa độ
(không trùng với gốc tọa độ ![]() ) sao cho
) sao cho ![]() là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác ![]() ?
?
Trong không gian , cho điểm
. Phương trình mặt phẳng
cắt trục
lần lượt tại
(không trùng với gốc tọa độ
) sao cho
là tâm đường tròn ngoại tiếp tam giác
?
Trong không gian với hệ tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() và
và ![]() . Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng
. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng ![]() là:
là:
Xét hệ phương trình
. Đặt
ta suy ra
.
Từ đó ta thu được phương trình đường thẳng:
Xét điểm , ta thấy
chỉ thuộc đường thẳng:
Tích phân  có giá trị là:
có giá trị là:
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và
và ![]() ,
, ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() . Chọn khẳng định sai trong các khẳng định sau?
. Chọn khẳng định sai trong các khẳng định sau?
Theo định nghĩa tích phân ta có: .
Phương trình nào dưới đây nhận hai số phức ![]() và
và ![]() là nghiệm ?
là nghiệm ?
Ta có và
.
Suy ra là nghiệm của phương trình
.
Tìm nguyên hàm ![]() .
.
Ta có:
Cho hai số phức ![]() . Tìm môđun của số phức
. Tìm môđun của số phức ![]() .
.
Ta có:
Tích phân  có giá trị là:
có giá trị là:
Tích phân có giá trị là:
Ngoài ra ta có thể kiểm tra bằng máy tính, dễ dàng thu được kết quả như cách trên.
Cho hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() , biết rằng
, biết rằng ![]() . Khi đó giá trị
. Khi đó giá trị ![]() là:
là:
Ta có:
Mà . Vậy với
thì
Vậy .
Tính góc của hai vectơ ![]()
Áp dụng công thức tính góc giữa 2 vecto, ta có:
Thay số suy ra được:
Cho số phức z thỏa mãn ![]() . Giá trị của
. Giá trị của ![]() là:
là:
Với
Với
Trong không gian với hệ toạ độ ![]() , cho ba điểm
, cho ba điểm ![]() . Tính khoảng cách
. Tính khoảng cách ![]() từ gốc toạ độ
từ gốc toạ độ ![]() đến mặt phẳng
đến mặt phẳng ![]() ?
?
Phương trình tổng quát của mặt phẳng có dạng:
Khoảng cách từ gốc tọa độ đến
là:
Cho hai số phức ![]() . Phần thực và phần ảo của số phức
. Phần thực và phần ảo của số phức ![]() tương ứng bằng:
tương ứng bằng:
Ta có:
Tính thể tích ![]() của vật thể sinh ra khi quay quanh trục
của vật thể sinh ra khi quay quanh trục ![]() hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số ![]() , đường thẳng
, đường thẳng ![]() và trục hoành?
và trục hoành?
Thể tích V của vật thể là:
Biết ![]() và
và ![]() là ba nghiệm của phương trình
là ba nghiệm của phương trình ![]() ,
,
trong đó ![]() là nghiệm có phần ảo dương. Phần ảo của số phức
là nghiệm có phần ảo dương. Phần ảo của số phức ![]() bằng:
bằng:
Xét phương trình là phương trình bậc ba với hệ số thực nên luôn có một nghiệm thực là
.
Do đó phương trình tương đương với:
.
Nên là hai nghiệm phức của phương trình bậc hai với hệ số thực (1).
Suy ra .
Khi đó : .
Vậy phần ảo của là
.
Cho đồ thị của hàm số ![]() như sau:
như sau:

Diện tích hình phẳng (phần tô đậm trong hình vẽ) được xác định bởi công thức:
Dựa vào hình vẽ ta được: .
Gọi ![]() và
và ![]() là hai nghiệm phức của phương trình:
là hai nghiệm phức của phương trình: ![]() . Tính
. Tính ![]() .
.
9 || chín || Chín
Gọi và
là hai nghiệm phức của phương trình:
. Tính
.
9 || chín || Chín
Ta có .
Vậy phương trình có hai nghiệm phức lần lượt là:
.
Do đó .
Tính tổng tất cả các nghiệm của phương trình sau: ![]() là?
là?
Đặt , khi đó phương trình đã cho có dạng:
Vậy phương trình đã cho có 4 nghiệm có tổng là
Trong không gian với hệ toạ độ ![]() , cho điểm
, cho điểm ![]() , đường thẳng
, đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() qua
qua ![]() vuông góc với d và song song với
vuông góc với d và song song với ![]() .
.
Đường thẳng có vec tơ chỉ phương
.
Mặt phẳng có vec tơ pháp tuyến
.
Đường thẳng ∆ vuông góc với nên vectơ chỉ phương
Đường thẳng ∆ song song với (P) nên
Ta có
Suy ra vec tơ chỉ phương của đường thẳng ∆ là
Vậy phương trình đường thẳng ∆ là .
Trong không gian ![]() , cho
, cho ![]() . Nếu ba vectơ
. Nếu ba vectơ ![]() đồng phẳng thì:
đồng phẳng thì:
Ta có:
Ba vectơ đồng phẳng
Cho hình hộp ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Hình vẽ minh họa
đúng vì
đúng vì
đúng vì
sai vì
Cho hàm số ![]() liên tục nhận giá trị dương trên
liên tục nhận giá trị dương trên ![]() và thỏa mãn
và thỏa mãn ![]() ;
; ![]() . Giá trị
. Giá trị ![]() gần nhất với giá trị nào sau đây?
gần nhất với giá trị nào sau đây?
Vì
Mà
Nghiệm của phương trình sau trên trường số phức là:![]()
Do tổng tất cả các hệ số của phương trình bằng 0 nên pt có nghiệm .
Vậy phương trình đã cho có 4 nghiệm:.
Cho số phức z thỏa mãn  . Viết z dưới dạng
. Viết z dưới dạng ![]() . Khi đó tổng
. Khi đó tổng ![]() có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
Tích phân  có giá trị là:
có giá trị là:
Ta có: và
Xét
Đặt
Đổi cận
Xét
Đặt
Đổi cận
Cho a, b, c là các số thực và ![]() . Giá trị của
. Giá trị của ![]() bằng:
bằng:
Cách 1: Ta có
và
.
Ta có
Cách 2: Chọn .
Ta có
Thử lại các đáp án với ta thấy chỉ có đáp án
thỏa mãn.
Cho tích phân  , a và b là các số hữu tỉ. Giá trị của
, a và b là các số hữu tỉ. Giá trị của ![]() là:
là:
Ta có:
, với
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Vectơ
. Vectơ ![]() có tọa độ là:
có tọa độ là:
Ta có:
Vậy đáp án đúng là: .
Cho hai đường thẳng (d1 ): ![]() và
và ![]()
Xét VTTĐ của (d1 ) và (d2 )? Tìm câu đúng ?
Chuyển đường thẳng (d1 ) và (d2 ) về dạng tham số :
có vectơ chỉ phương
và qua
.
có vectơ chỉ phương
và hệ phương trình
vô nghiệm.
.
Số phức liên hợp của số phức 3 - 4i là:
=
= a – bi
Cho ![]() . Giá trị của x và y bằng:
. Giá trị của x và y bằng:
Ta có:
Tìm nguyên hàm của hàm của hàm số ![]()
Tìm nguyên hàm ![]() của hàm số
của hàm số ![]() , biết rằng
, biết rằng ![]() ?
?
Ta có:
Vậy .
Tìm nghiệm của phương trình sau trên tập số phức ![]() :
: ![]() (1)
(1)
Kiểm tra nghiệm ta dễ dàng nhận xét
không là nghiệm của phương trình đã cho vậy
.
Chia hai vế PT (1) cho z2 ta được : (2)
Đặt . Khi đó
Phương trình (2) có dạng : (3)
Vậy PT (3) có 2 nghiệm:
Với , ta có
(4)
Có
Vậy PT(4) có 2 nghiệm :
;
Do đó PT đã cho có 4 nghiệm :
Họ nguyên hàm của hàm số ![]() là:
là:
Ta có:
.
Cho hình lập phương ![]() ; đáy là hình vuông cạnh
; đáy là hình vuông cạnh ![]() . Trên cạnh
. Trên cạnh ![]() lần lượt lấy các điểm
lần lượt lấy các điểm ![]() sao cho
sao cho ![]() . Tính số đo góc giữa hai đường thẳng
. Tính số đo góc giữa hai đường thẳng ![]() và
và ![]() .
.
Cho hình lập phương ; đáy là hình vuông cạnh
. Trên cạnh
lần lượt lấy các điểm
sao cho
. Tính số đo góc giữa hai đường thẳng
và
.
Số phức ![]() có phần thực bằng
có phần thực bằng
Số phức z = a + bi có b được gọi là phần thực.
