Số nghiệm của phương trình ![]() là
là
Điều kiện:
Phương trình tương đương:
Kết hợp điều kiện ta được: thỏa mãn điều kiện
Vậy phương trình đã cho có một nghiệm.
Số nghiệm của phương trình ![]() là
là
Điều kiện:
Phương trình tương đương:
Kết hợp điều kiện ta được: thỏa mãn điều kiện
Vậy phương trình đã cho có một nghiệm.
Dấu của tam thức bậc 2: f(x) = –x2+ 5x – 6 được xác định như sau:
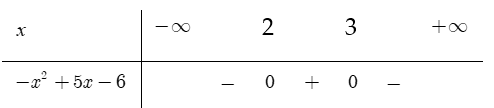
Dựa vào bảng xét dấu, ta chọn đáp án f(x) > 0với 2< x < 3 và f(x) < 0với x < 2 ∨ x > 3 .
Hệ số của ![]() trong khai triển
trong khai triển ![]() là:
là:
Ta có số hạng tổng quát:
Số hạng chứa nên
Vậy hệ số của trong khai triển đã cho là:
.
Phương trình tham số của đường thẳng đi qua hai điểm ![]() là:
là:
Vectơ chỉ phương:
Đường thẳng đi qua điểm và có vectơ chỉ phương
nên có phương trình tham số là:
Một nhóm học sinh gồm 6 nam và 4 nữ. Cần chọn ra một nhóm 5 người gồm cả nam và nữ đi trực nhật. Hỏi có bao nhiêu cách chọn nếu số bạn nữ luôn nhiều hơn số bạn nam.
Trường hợp 1: 4 nữ, 1 nam
Chọn 4 nữ từ 4 nữ và 1 nam từ 6 nam, có: (cách).
Trường hợp 2: 3 nữ, 2 nam, có: (cách).
Vậy có (cách).
Một vectơ chỉ phương của đường thẳng ![]() là:
là:
Đường thẳng có một vectơ chỉ phương là:
Tìm tập xác định D của hàm số ![]()
Hàm số xác định khi và chỉ khi
Phương trình x2 + 2x + 3 = 0 ⇔ x ∈ ⌀ và
Bảng xét dấu
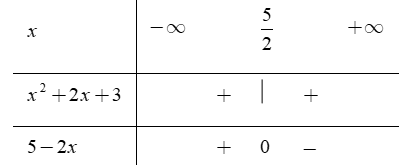
Dựa vào bảng xét dấu ta thấy
Vậy tập xác định của hàm số là
Trong hệ tọa độ ![]() cho bốn điểm
cho bốn điểm ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Ta có ngược hướng.
Số nghiệm của phương trình:![]() là
là
Điều kiện xác định của phương trình x ≥ 4.
Phương trình tương đương với
.
Kết hợp điều kiện suy ra .
Vậy phương trình có hai nghiệm.
Tổng tất cả các giá trị của tham số ![]() thỏa mãn
thỏa mãn ![]() bằng:
bằng:
Điều kiện
Ta có:
Tổng tất cả các giá trị của tham số thỏa mãn
bằng
.
Câu lạc bộ cầu lông gồm 12 tay vợt nam và 9 tay vợt nữ. Hỏi có bao nhiêu cách lập đội đôi nam nữ từ câu lạc bộ để tham gia giải đấu giao lưu các trường?
Có 12 cách chọn 1 tay vợt nam
Ứng với mỗi cách chọn 1 tay vợt nam ta có 9 cách chọn một tay vợt nữ
Theo quy tắc nhân ta có: 9.12 = 108 cách chọn một đôi nam nữ tham gia giải đấu.
Cho hai đường thẳng ![]() và
và ![]() . Tính góc hợp bởi hai đường thẳng đã cho?
. Tính góc hợp bởi hai đường thẳng đã cho?
Ta có:
Vectơ pháp tuyến của đường thẳng là:
Vectơ pháp tuyến của đường thẳng là:
Ta có:
Vậy góc hợp bởi hai đường thẳng bằng .
Biến đổi biểu thức ![]() dưới dạng
dưới dạng ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có:
Trong hệ tọa độ ![]() cho ba điểm
cho ba điểm ![]() Tìm tọa độ điểm
Tìm tọa độ điểm ![]() để tứ giác
để tứ giác ![]() là hình bình hành.
là hình bình hành.
Gọi Ta có
Tứ giác là hình bình hành
Trong mặt phẳng tọa độ ![]() cho hai vectơ
cho hai vectơ ![]() và
và ![]() . Tính cosin của góc giữa hai vectơ
. Tính cosin của góc giữa hai vectơ ![]() và
và ![]()
Ta có: .
Các giá trị m để tam thức ![]() đổi dấu 2 lần là:
đổi dấu 2 lần là:
Để đổi dấu 2 lần thì
.
Ta có:
hoặc
.
Trong mặt phẳng tọa độ ![]() cho vectơ
cho vectơ ![]() . Vectơ nào sau đây không vuông góc với vectơ
. Vectơ nào sau đây không vuông góc với vectơ ![]() ?
?
Vì nên đáp án
đúng.
Vì nên đáp án
đúng.
Vì nên đáp án
sai.
Vì nên đáp án
đúng.
Có thể lập được bao nhiêu số tự nhiên lẻ có ba chữ số đôi một khác nhau?
Gọi số tự nhiên có ba chữ số có dạng
=> Có 5 cách.
=> Có 8 cách.
=> Có 8 cách.
=> Số các số được tạo thành là: số.
Cho ![]() Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
Ta có và
Xét tỉ số và
không cùng phương. Loại
và
ngược hướng.
Xét tỉ số không cùng phương. Loại
cùng phương.
Xét tỉ số và
cùng hướng. Chọn
và
cùng hướng.
Trong mặt phẳng tọa độ ![]() cho tọa độ hai điểm
cho tọa độ hai điểm ![]() . Tính tọa độ vecto
. Tính tọa độ vecto ![]() ?
?
Ta có:
Vậy .
Khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() bằng:
bằng:
Nghiệm của bất phương trình ![]() có
có
Ta có:
Bảng xét dấu
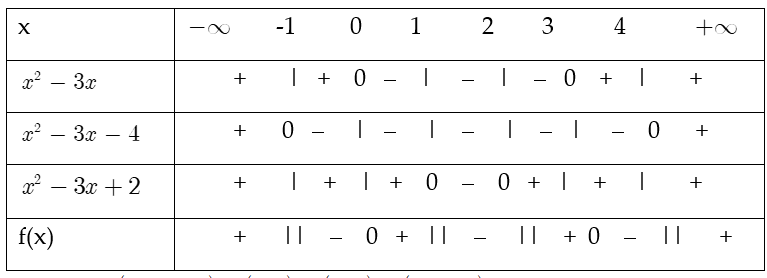
f(x) > 0 ⇔ x ∈ (−∞;−1) ∪ (0;1) ∪ (2;3) ∪ (4;+∞)
Biết phương trình ![]() có nghiệm duy nhất là
có nghiệm duy nhất là ![]() . Hãy chọn khẳng định đúng.
. Hãy chọn khẳng định đúng.
ĐK
.
Trong mặt phẳng tọa độ ![]() cho hai điểm
cho hai điểm ![]() và
và ![]() Tìm
Tìm ![]() thuộc trục tung sao cho
thuộc trục tung sao cho ![]() nhỏ nhất.
nhỏ nhất.
Vì .
Ta có:
Ta có:
Suy ra nhỏ nhất khi và chỉ khi
.
Cho tam giác ![]() có
có ![]() ,
,![]() ,
,![]() .Tính
.Tính ![]() .
.
Ta có ,
suy ra
.
Cho tam giác ![]() cân tại
cân tại ![]() ,
, ![]() và
và ![]() . Tính
. Tính ![]() .
.
Ta có .
Giả sử phương trình đường thẳng ![]() với
với ![]() và
và ![]() là phân số tối giản. Biết rằng đường thẳng
là phân số tối giản. Biết rằng đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và cách điểm
và cách điểm ![]() một khoảng bằng
một khoảng bằng ![]() . Khi đó giá trị biểu thức
. Khi đó giá trị biểu thức ![]() là:
là:
Ta có:
Với thì
(loại do
)
Xét thì
Với thì ta chọn
Vậy
Trong hệ trục tọa độ ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Ta có:
Tìm khẳng định đúng trong các khẳng định sau?
Tam thức bậc 2 là biểu thức f(x) có dạng ax2+ bx + c (a≠0).
f(x) = 3x2 − 5 là tam thức bậc 2 với a = 3, b = 0, c = − 5.
Số cách lấy một chiếc bút trong hộp gồm 4 chiếc bút bi và 6 chiếc bút máy bằng:
Áp dụng quy tắc cộng ta có số cách lấy một chiếc bút là:
cách.
Cho hai đường thẳng ![]() và
và ![]() với m là tham số. Tìm giá trị của tham số m để hai đường thẳng tạo với nhau một góc bằng nửa góc vuông?
với m là tham số. Tìm giá trị của tham số m để hai đường thẳng tạo với nhau một góc bằng nửa góc vuông?
VTPT của hai đường thẳng lần lượt là
Để hai đường thẳng tạo với nhau một góc bằng thì
Vậy .
Có tất cả bao nhiêu cách xếp ![]() quyển sách khác nhau vào một hàng ngang trên giá sách?
quyển sách khác nhau vào một hàng ngang trên giá sách?
Mỗi cách sắp xếp quyển sách khác nhau vào một hàng ngang trên giá sách là một hoán vị của
phần tử. Vậy số cách sáp xếp là
.
Xác định vị trí tương đối của hai đường thẳng ![]() và
và ![]() ?
?
Ta có: suy ra hai đường thẳng (d) và (d’) song song với nhau.
Cho hai số tự nhiên ![]() sao cho
sao cho ![]() . Chọn khẳng định đúng sau đây?
. Chọn khẳng định đúng sau đây?
Khẳng định đúng là: .
Khai triển biểu thức ![]() ta được:
ta được:
Ta có:
Trong mặt phẳng tọa độ ![]() , cho đường thẳng
, cho đường thẳng ![]() . Hãy chỉ ra một vectơ pháp tuyến của đường thẳng
. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ![]() ?
?
Ta có: Vectơ pháp tuyến của đường thẳng là:
.
Trong mặt phẳng tọa độ ![]() , cho hình chữ nhật
, cho hình chữ nhật ![]() có
có ![]() . Gọi trung điểm các cạnh
. Gọi trung điểm các cạnh ![]() lần lượt là
lần lượt là ![]() . Điểm
. Điểm ![]() là tọa độ giao điểm của
là tọa độ giao điểm của ![]() và
và ![]() , phương trình đường thẳng
, phương trình đường thẳng ![]() . Xác định tọa độ điểm C, biết hoành độ điểm C nhỏ hơn 3?
. Xác định tọa độ điểm C, biết hoành độ điểm C nhỏ hơn 3?
Hình vẽ minh họa
Từ giả thiết ta có: nên
là hình vuông, do đó
Gọi thì
là trung điểm của
Khi đó là trọng tâm tam giác CNM khi đó
Phương trình đường thẳng BE đi qua E và vuông góc CM là
Khi đó tọa độ điểm I là nghiệm của hệ phương trình:
Do
Gọi ta có:
(vì
).
Điểm nào sau đây không thuộc đường thẳng ![]() ?
?
Gọi
Chọn .
Cho tập ![]() gồm
gồm ![]() phần tử. Số tập con gồm
phần tử. Số tập con gồm ![]() phần tử của M là:
phần tử của M là:
Số tập con gồm phần tử của
là số cách chọn
phần tử bất kì trong
phần tử của
.
Do đó số tập con gồm phần tử của
là
.
