Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2)

Đề thi giữa HK2 Toán 8 được biên soạn chuẩn ma trận đề thi gồm các câu hỏi trắc nghiệm và tự luận bám sát chương trình sách Chân trời sáng tạo, giúp bạn học củng cố kiến thức chuẩn bị cho kì thi sắp tới

Khoahoc Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2) 5,0

Mời các bạn học cùng thử sức với Đề thi giữa học kì 2 môn Toán lớp 8 - có đáp án theo chương trình sách Chân trời sáng tạo nha!

Đề thi giữa học kì 2 Toán lớp 8 CTST

PHÒNG GD&ĐT …….

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

Thời gian: 90 phút (không kể thời gian phát đề)

I. Trắc nghiệm (4,0 điểm)

(Hãy chọn các đáp án đúng nhất trong các đáp án sau)

Câu 1. Đồ thị hàm số $y = - 3x + 1$ và điểm $C$ thuộc đồ thị hàm số. Tìm tọa độ điểm $C$ biết tung độ điểm $C$ bằng $1$ ?

A. $C( - 1;1)$	B. $C(0;0)$
C. $C(0;1)$	D. $C(1;0)$

Câu 2. Cho hàm số $y = f(x) = \frac{2x - 5}{3}$ . Giá trị của $f( - 1);f(2)$ lần lượt là:

A. $- 1; - \frac{5}{3}$	B. $- \frac{7}{3}; - \frac{1}{3}$
C. $\frac{7}{3}; - \frac{1}{3}$	D. $\frac{- 7}{3};\frac{1}{3}$

Câu 3. Cho hàm số $y = 4x + 20$ . Với giá trị nào của $x$ thì $f(x) = 300$ ?

A. $x = 7$	B. $x = 70$
C. $x = 17$	D. $x = 140$

Câu 4. Hình vẽ dưới đây là đồ thị của hàm số nào?

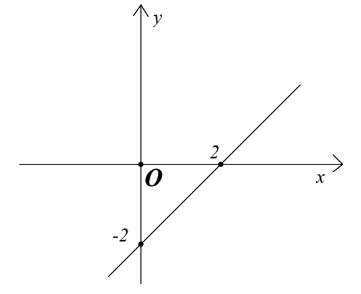
Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2)

A. $y = - x - 2$	B. $y = x - 2$
C. $y = - x + 2$	D. $y = 2x - 2$

Câu 5. Đồ thị hàm số $y = ax + b;(a \neq 0)$ cắt trục tung tại điểm có tung độ bằng $5$ và đi qua điểm $A(1;6)$ . Khi đó:

A. $a = 1;b = 6$	B. $a = 5;b = 1$
C. $a = 1;b = 5$	D. $a = 6;b = 1$

Câu 6. Đường thẳng $3y + 6x + 7 = 0$ có hệ số góc là:

A. $6$

B. $- 2$

C. $2$

D. $- 6$

Câu 7. Trong các đường thẳng sau, đường thẳng nào song song với trục hoành?

A. $x = - 5y$	B. $y = - 5x$
C. $y = - 5$	D. $x = - 5$

Câu 8. Với giá trị nào của tham số m thì đồ thị của hai hàm số $y = x + (5 + m)$ và $y = 2x + (7 - m)$ cắt nhau tại một điểm nằm trên trục hoành?

A. $m = 1$	B. $m = \pm 1$
C. $m \neq \pm 1$	D. $m = - 1$

Câu 9. Nghiệm của phương trình $3x - 2 = 2x - 3$ là:

A. $x = - 1$	B. $x = 1$
C. $x = 2$	D. $x = - 2$

Câu 10. Phương trình $x(x - 4) - x^{2} + 3mx = 2mx^{2}$ với (m là tham số) nhận $x = 1$ là nghiệm khi:

A. $m = 4$	B. $m = \frac{1}{4}$
C. $m = - \frac{1}{4}$	D. $m = - 4$

Câu 11. Cho tứ giác $ABCD$ . Gọi $E;F;G;H$ lần lượt là trung điểm các cạnh $AB,BC,CD,DA$ biết $BD = 18cm$ . Tổng độ dài hai đoạn thẳng $HE$ và $GF$ là:

A. $18cm$	B. $9cm$
C. $36cm$	D. $27cm$

Câu 12. Quan sát hình vẽ và chọn khẳng định đúng.

Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2)

A. $\frac{AB}{EC} = \frac{AD}{AE} \Rightarrow DE//BC$	B. $\frac{AC}{AB} = \frac{AE}{AD} \Rightarrow DE//BC$
C. $\frac{BA}{AD} = \frac{AC}{CE} \Rightarrow DE//BC$	D. $\frac{AD}{DE} = \frac{AE}{DE} \Rightarrow DE//BC$

Câu 13. Cho tam giác MNP có MA là phân giác ngoài góc M (như hình vẽ).

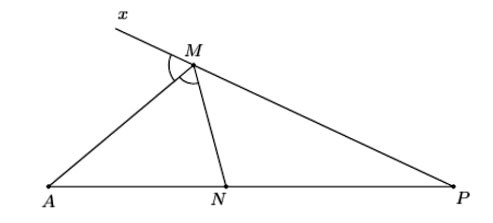
Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2)

Biết $\frac{AN}{AP} = \frac{3}{4}$ . Kết luận nào sau đây đúng?

A. $\frac{AB}{AC} = \frac{BE}{CE}$	B. $\frac{MN}{MP} = 3$
C. $\frac{MN}{MP} = \frac{1}{3}$	D. $\frac{MN}{MP} = \frac{3}{4}$

Câu 14. Cho tam giác ABC vuông tại A. Tính độ dài đường trung bình ứng với cạnh BC, biết rằng $AB = 6cm,AC = 8cm$ ?

A. $BC = 10cm$	B. $BC = 5cm$
C. $BC = 20cm$	D. $BC = 7cm$

Câu 15. Tìm x trong hình vẽ:

Đề thi giữa học kì 2 Toán lớp 8 Chân trời sáng tạo năm học 2023 - 2024 (Đề 2)

A. $x = 5,1$	B. $x = 14,2$
C. $x = 8,1$	D. $x = 2,1$

II. TỰ LUẬN: (6,0 điểm)

Câu 1: Giải các phương trình sau:

a) $8 - 4x = 0$	b) $\frac{1}{2}(x + 5) - 4 = \frac{1}{3}(2x - 1)$
c) $1 - \frac{x + 5}{3} = \frac{3(x - 1)}{4}$	d) $\frac{x - 1}{2015} + \frac{x - 3}{2013} = \frac{x - 5}{2011} + \frac{x - 7}{2009}$

Câu 2. Cho hàm số $y = mx + 1\ \ \ (*)$ với $m$ là tham số.

a) Tìm m để đồ thị hàm số đi qua điểm $A(1;4)$ . Với giá trị m vừa tìm được, vẽ đồ thị hàm số và nhận xét về góc tạo bởi đồ thị hàm số $(*)$ tạo với trục $Ox$ ?

b) Tìm m để đồ thị hàm số $(*)$ song song với đường thẳng $(d):y = m^{2}x + m + 1$ .

Câu 3. Cho hình chữ nhật $ABCD$ tâm O. Gọi $M,N$ lần lượt là trung điểm các cạnh $AD,BC$ . Trên tia đối của tia $DC$ lấy điểm $P$ , $MP$ giao với $AC$ tại $Q$ và cắt $BC$ tại $S$ . Gọi $R$ là giao điểm của $QN$ và $DC$ . Chứng minh rằng: