Đề thi giữa học kì 2 Toán lớp 8 Kết nối tri thức năm học 2023 - 2024 (Đề 5)

Đề thi giữa HK2 Toán 8 được biên soạn chuẩn ma trận đề thi gồm các câu hỏi trắc nghiệm và tự luận bám sát chương trình sách Kết nối tri thức, giúp bạn học củng cố kiến thức chuẩn bị cho kì thi sắp tới

Khoahoc Đề thi giữa học kì 2 Toán lớp 8 Kết nối tri thức năm học 2023 - 2024 (Đề 5) 5,0

Mời các bạn học cùng thử sức với Đề thi giữa học kì 2 môn Toán lớp 8 - có đáp án theo chương trình sách Kết nối tri thức nha!

Đề thi giữa học kì 2 Toán lớp 8 Kết nối tri thức

PHÒNG GD&ĐT …….

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

Thời gian: 90 phút (không kể thời gian phát đề)

I. TRẮC NGHIỆM: (4,0 điểm)

*Chọn và khoanh tròn chữ cái trước câu trả lời đúng nhất.

Câu 1. Kết quả rút gọn phân thức $\frac{2x(x + 1)}{4(x + 1)}$ là:

A. $2x$	B. $\frac{x}{2}$
C. $\frac{2}{x}$	D. $\frac{1}{2}$

Câu 2. Mẫu thức chung của hai phân thức $\frac{3 - x}{x(x + 3)}$ và $\frac{4}{(x - 3)(x + 3)}$ là:

A. $x(x - 3)^{2}$	B. $x(x + 3)^{2}$
C. $x\left( 9 - x^{2} \right)$	D. $x\left( x^{2} - 9 \right)$

Câu 3. Kết quả của phép tính $\frac{x^{2}}{x - 2} - \frac{1 - 3x}{2 - x}$ là:

A. $\frac{x^{2} - 3x - 1}{x - 2}$	B. $\frac{x^{2} - 3x + 1}{x - 2}$
C. $\frac{- x^{2} - 3x - 1}{2 - x}$	D. $\frac{x^{2} + 3x - 1}{2 - x}$

Câu 4. Điều kiện để phân thức $\frac{3x - 5}{x(x + 2)}$ xác định là:

A. $x \neq 0$	B. $x \neq - 2$
C. $x \neq 0;x \neq - 2;x \neq - \frac{5}{3}$	D. $x \neq 0;x \neq - 2$

Câu 5. Biến đổi biểu thức hữu tỉ $\dfrac{\dfrac{x + 1}{x - 2}}{\dfrac{3(x + 1)}{x +2}}$ ta được phân thức:

A. $\frac{1}{3}$	B. $\frac{x + 2}{x - 2}$
C. $\frac{x + 1}{3(x - 2)}$	D. $\frac{x - 2}{x + 2}$

Câu 6. Tìm đa thức Q thỏa mãn $\frac{5(y - x)^{2}}{5x^{2} - 5xy} = \frac{x - y}{Q}$ (các phân thức đều có nghĩa)?

A. $Q = x$	B. $Q = 5(x - y)$
C. $Q = 5(y - x)$	D. $Q = x + y$

Câu 7. Với điều kiện nào dưới đây để $\Delta MNP\sim\Delta HIK$ ?

A. $\frac{HI}{NP} = \frac{HK}{MP} = \frac{IK}{MN}$	B. $\frac{HI}{MN} = \frac{HK}{MP} = \frac{IK}{NP}$
C. $\frac{HI}{NP} = \frac{HK}{MN} = \frac{IK}{MP}$	D. $\frac{HI}{MP} = \frac{HK}{MN} = \frac{IK}{NP}$

Câu 8. Cho tam giác $ABC$ có $\widehat{A} = 90^{0};AH\bot BC$ . Hệ thức nào dưới đây đúng?

A. $AB = BC.BH$	B. $AC^{2} = CH.BH$
C. $AH^{2} = BH.CH$	D. $AH = CH.BH$

Câu 9. Với giá trị nào của tham số m thì hai phương trình $- 2x + 1 = 0$ và $mx - 1 = 3$ tương đương với nhau?

A. $m = 8$	B. $m = 2$
C. $m = - 8$	D. $m = - 2$

Câu 10. Trong các phương trình sau đây, phương trình nào là phương trình bậc nhất một ẩn?

A. $\frac{1}{x} + 2 = 0$	B. $2x^{2} + 1 = 0$
C. $0x - 8 = 0$	D. $x - 1 = 7$

Câu 11. Giá trị $x = 2$ là nghiệm của phương trình nào sau đây?

A. $5x - 2 = 4x$	B. $x + 5 = 2x - 2$
C. $3x + 3 = x - 1$	D. $x + 1 = 2x - 2$

Câu 12. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:

A. $11cm,8cm,7cm$	B. $12dm,15dm,18dm$
C. $9m,12m,15m$	D. $6m,7m,9m$

Câu 13. Tìm x:

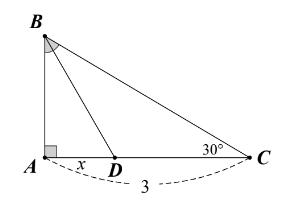
Đề thi giữa học kì 2 Toán lớp 8 Kết nối tri thức năm học 2023 - 2024 (Đề 5)

A. $x = 2$	B. $x = \frac{3}{2}$
C. $x = 1$	D. $x = \frac{6}{5}$

Câu 14. Chọn khẳng định sai?

A. Hai tam giác bằng nhau thì đồng dạng.

B. Hai tam giác đều luôn đồng dạng với nhau.

C. Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và cặp cạnh tương ứng tỉ lệ.

D. Hai tam giác vuông luôn đồng dạng với nhau.

Câu 15. Nếu $\Delta ABC\sim\Delta DEF$ theo tỉ số đồng dạng $k = \frac{2}{5}$ thì tam giác $DEF$ đồng dạng với tam giác $ABC$ theo tỉ số đồng dạng là:

A. $k = 2$

B. $k = \frac{5}{2}$

C. $k = \frac{2}{5}$

D. $k = 5$

II. TỰ LUẬN: (6,0 điểm)

Câu 1: Tìm x biết:

a) $2x + 1 = 5$	b) $(2x - 3) - (3x + 4) = x + 5$
c) $\frac{x}{3} - \frac{2x + 1}{2} = \frac{x}{6} - x$	d) $\frac{x - 1}{99} + \frac{x - 2}{98} + \frac{x - 3}{97} + \frac{x - 4}{96} = 4$