Con lắc đơn

Con lắc đơn gồm một vật nhỏ khối lượng m, treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, có chiều dài l.

  • Vị trí cân bằng của con lắc là vị trí mà dây treo có phương thẳng đứng.
  • Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu của vật.

II. Khảo sát dao động của con lắc đơn về mặt động lực học

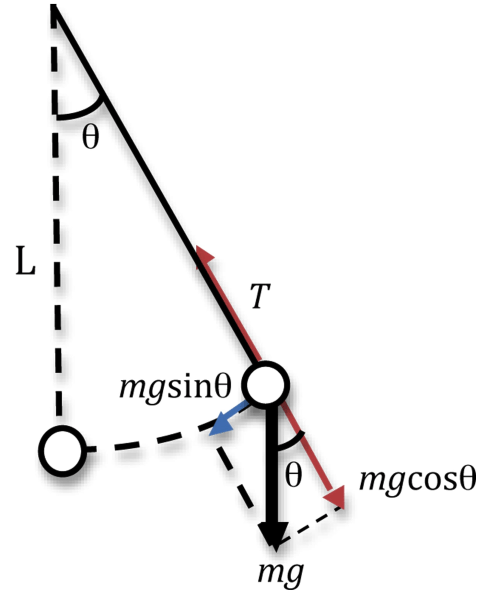
Con lắc đơn

  • Trong khi dao động của vật chịu tác dụng của trọng lực \overrightarrow P và lực căng \overrightarrow F
  • Hợp lực của lực căng \overrightarrow F và lực thành phần \overrightarrow {{P_n}} đóng vai trò là lực hướng tâm giữ cho vật chuyển động trên cung tròn
  • Lực thành phần \overrightarrow {{P_t}} là lực kéo về có giá trị: {P_t} = - m.g.\sin \theta

Nếu góc \theta nhỏ thì \sin \theta \approx \theta

{P_t} = - m.g.\theta = - m.g.\frac{x}{l}

  • Vậy khi dao động nhỏ, con lắc đơn dao động điều hòa theo phương trình:

x = {x_0}.\cos \left( {\omega t + \varphi } \right)

Với chu kì T = 2\pi \sqrt {\frac{l}{g}}, trong đó {x_0} = l.{\theta _0} là biên độ dao động.

III. Khảo sát sự biến thiên của con lắc đơn về mặt năng lượng

  • Động năng của con lắc:

{W_d} = \frac{1}{2}m{v^2}

  • Thế năng của con lắc:

{W_t} = m.g.l\left( {1 - \cos \theta } \right)

  • Nếu bỏ qua ma sát thì cơ năng của con lắc được bảo toàn:

\begin{matrix} W = {W_d} + {W_t} \hfill \\ = \dfrac{1}{2}m{v^2} + m.g.l\left( {1 - \cos \theta } \right) = const \hfill \\ \end{matrix}