Lớp 10 Vật lí 10 - Chân trời sáng tạo

Lý thuyết Vật lý 10 bài 20: Động học của chuyển động tròn CTST

Lý thuyết Vật lý lớp 10 bài 20: Động học của chuyển động tròn được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Vật lý lớp 10 sách chân trời sáng tạo. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

1. Định nghĩa radian -Số đo cung tròn theo góc

a. Định nghĩa radian

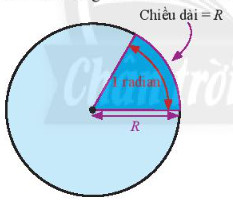
1 rad là số đo góc ở tâm một đường tròn chắn cung có độ dài bằng bán kính đường tròn đó. 

1\,rad = \frac{{{{180}^o}}}{\pi } = \frac{{{{180}^o}}}{{3,1416...}} \approx 57,{2958^o}

Ví dụ:

Minh họa góc có số đo 1 rad

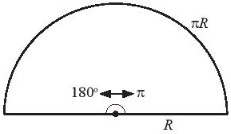
 Minh họa góc \pirad

Các hệ thức chuyển đổi đơn vị từ độ sang radian và từ radian sang độ:

{a_{\left( {radian} \right)}} = {a_{\left( {do} \right)}}.\frac{\pi }{{{{180}^o}}}

{a_{\left( {do} \right)}} = {a_{\left( {radian} \right)}}.\frac{{{{180}^o}}}{\pi }

b. Mối liên hệ giữa cung tròn và góc

Một trong các lí do để sử dụng đơn vị radian thay vì độ là ta có thể xác định được hệ thức liên hệ trực tiếp giữa chiều dài của một cung tròn và số đo góc ở tâm chắn cung (theo đơn - vị radian).

Mối liên hệ giữa độ dài cung tròn và góc chắn cung đo bằng rad

Khi góc chắn cung có số đo là α (radian) thì chiều dài cung tròn sẽ bằng

s = {\alpha _{\left( {radian} \right)}}.R

Ví dụ: Tìm chiều dài của một cung tròn của đường tròn có bán kính 0,5 m, được chắn bởi góc 600?

Hướng dẫn giải:

Đổi góc {60^0} = \frac{\pi }{3}\,rad

Ta có: s = {\alpha _{rad}}.R = \frac{\pi }{3}.0,5 = 0,5236\left( m \right)

2. Tốc độ trong chuyển động tròn

a. Chuyển động tròn

Chuyển động tròn là một trong những loại chuyển động ta thường thấy trong đời sống: một điểm trên cánh quạt chuyển động theo một đường tròn khi cánh quạt quay, chuyển động của một vệ tinh nhân tạo xung quanh Trái Đất, ....

Cabin của đu quay chuyển động tròn

Định nghĩa: Một chất điểm chuyển động tròn khi có quỹ đạo là đường tròn.

b. Tốc độ góc trong chuyển động tròn

Tốc độ góc trong chuyển động tròn có giá trị bằng góc quay được bởi bán kính trong một đơn vị thời gian:

\omega = \frac{{\Delta \alpha }}{{\Delta t}}

Trong đó (tính theo rad) là độ dịch chuyển góc hay góc quét bởi bán kính R sau khoảng thời gian Δt (tính theo s): \Delta \alpha  = \alpha  - {\alpha _o}

  • Tốc độ góc ω có đơn vị: rad/s. Ngoài ra, còn có các đơn vị khác như vòng/s, độ/s,..
  • Chuyển động tròn đều có tốc độ góc không đổi.

c. Vận dụng tốc độ góc

Ví dụ: Hãy so sánh tốc độ góc của kim giây và kim phút của một đồng hồ (Hình 20.8). Giả sử rằng các kim này quay đều.

Hướng dẫn

Xem kim giây quay đều không giật. Thời gian kim giây và kim phút quay được 1 vòng (2rad) là:

Tg = 1 phút = 60s; Tph = 60 phút = 3600 s

Tốc độ góc của kim giây:

{\omega _g} = \frac{{\Delta \alpha }}{{\Delta t}} = \frac{{2\pi }}{{{T_g}}} = \frac{{2\pi }}{{60}} = \frac{\pi }{{30}}rad/s

Tốc độ của kim phút:

{\omega _{ph}} = \frac{{\Delta \alpha }}{{\Delta t}} = \frac{{2\pi }}{{{T_g}}} = \frac{{2\pi }}{{3600}} = \frac{\pi }{{1800}}rad/s

Vậy: {\omega _g} > {\omega _{ph}}, do đó chuyển động của kim giây nhanh hơn chuyển động của kim phút (gấp 60 lần)

d. Vận tốc trong chuyển động tròn

Tốc độ của một chất điểm chuyển động tròn được tính bằng quãng đường mà chất điểm di chuyển được trong một đơn vị thời gian, theo hệ thức:

v = \frac{s}{{\Delta t}}

- Từ biểu thức của tốc độ góc rút ra được biểu thức mối liên hệ giữa tốc độ và tốc độ góc: v = R.\omega

Trong đó, R là bán kính của chuyển động tròn

Đơn vị: Khi ω tính theo đơn vị rad/s, R có đơn vị là m thì đơn vị của v là m/s

Vận tốc của chuyển động trong đều có

  • Phương: Tiếp tuyến với quỹ đạo (đường tròn).
  • Chiều: Theo chiều chuyển động.
  • Độ lớn: Không đổi, bằng v=ω.R.

3. Gia tốc hướng tâm của chuyển động tròn đều

a. Gia tốc hướng tâm

Gia tốc hướng tâm của chuyển động tròn đều có đặc điểm:

  • Phương: Trùng với bán kính.
  • Chiều: Hướng về tâm của vòng tròn quỹ đạo (nên có tên là gia tốc hướng tâm).
  • Độ lớn: Không đổi và bằng {a_{ht}} = \frac{{{v^2}}}{R} = {\omega ^2}.R.

b. Vận dụng gia tốc hướng tâm

Ví dụ: Một bánh xe đạp có đường kính bằng 62,2 cm, quay đều với tốc độ 7 vòng/s. Tính gia tốc hướng tâm của một điểm trên vành bánh xe.

Hướng dẫn giải

Tốc độ của bánh xe: \omega  = 7.2\pi  = 43,98rad/s

Gia tốc hướng tâm: {a_{ht}} = {\omega ^2}.R = \frac{{0,622}}{2}.{\left( {43,98} \right)^2} = 601,5m/{s^2}

Ví dụ: Kim giây của một đồng hồ dài 2,5 cm. Độ lớn gia tốc hướng tâm của đầu mút kim giây là bao nhiêu?

Hướng dẫn giải

Thời gian kim giây quay được một vòng là T = 60 s

{\omega _{gi}} = \frac{{\Delta \alpha }}{{\Delta t}} = \frac{{2.\pi }}{{60}} = \frac{\pi }{{30}}\left( {rad/s} \right)

Độ lớn gia tốc hướng tâm của kim giây là

{a_{ht}} = \frac{{{\nu ^2}}}{R} = {\omega ^2}.R = {\left( {\frac{\pi }{{30}}} \right)^2}.2,{5.10^{ - 2}} = 2,{74.10^{ - 4}}\left( {m/{s^2}} \right)

  • 284 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Vật Lí 10 CTST