Lớp 11 Vật Lí 11

Luyện tập Chương 7: Mắt, Các dụng cụ quang

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 19 câu
  • Điểm số bài kiểm tra: 19 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tác dụng của lăng kính

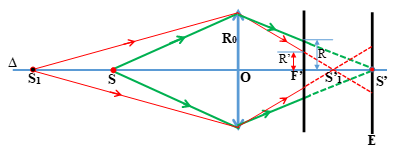
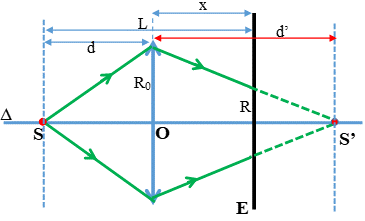
    Lăng kính có tác dụng

    Hướng dẫn:

    Máy quang phổ là dụng cụ dùng để phân tích chùm ánh sáng có nhiều thành phần thành những thành phần đơn sắc khác nhau. Nó dùng để nhận biết các thành phần cấu tạo của một chùm sáng phức tạp do một nguồn sáng phát ra.

    Nguyên tắc hoạt động: dựa trên hiện tượng tán sắc ánh sáng.

    Bộ phận của máy làm nhiệm vụ tán sác ánh sáng là: lăng kín

  • Câu 2: Nhận biết
    Tác dụng của kính lúp

    Kính lúp dụng để quan sát các vật có kích thước

    Hướng dẫn:

     Kính lúp dụng để quan sát các vật có kích thước nhỏ.

  • Câu 3: Nhận biết
    Chọn phát biểu sai

    Khi nói về cách sử dụng kính lúp, phát biểu nào sau đây sai?

    Hướng dẫn:

    Điều chỉnh và sử dụng kính lúp là sự điều chỉnh vị trí giữa vật và kính lúp, để ảnh của vật qua kính lúp đó là ảnh ảo (ta phải đặt vật trong khoảng tiêu cự của kính) sao cho nó nằm trong giới hạn thấy rõ của mắt người quan sát.

  • Câu 4: Nhận biết
    Chọn đáp án đúng

    Số bội giác của kính lúp hoặc kính hiển vi phụ thuộc khoảng nhìn rõ ngắn nhất Đ của người quan sát, còn với kính thiên văn hoặc ống nhòm thì không phụ thuộc vào Đ vì

    Hướng dẫn:

    Số bội giác của kính lúp hoặc kính hiển vi phụ thuộc khoảng nhìn rõ ngắn nhất Đ của người quan sát, còn với kính thiên văn hoặc ống nhòm thì không phụ thuộc vào Đ vì tính chất đặc biệt của dụng cụ quang.

  • Câu 5: Nhận biết
    Chọn đáp án chính xác

    Số bội giác thu được với kính hiển vi tốt, loại đắt tiền có thể thay đổi được trong phạm vi rộng là nhờ

    Hướng dẫn:

    Số bội giác thu được với kính hiển vi tốt, loại đắt tiền có thể thay đổi được trong phạm vi rộng là nhờ có nhiều vật kính và thị kính khác nhau.

  • Câu 6: Thông hiểu
    Chọn phương án đúng

    Số bội giác của kính thiên văn khi ngắm chừng ở vô cực

    Hướng dẫn:

    Khi ngắm chừng ở vô cực ta có:

    \left\{ {\begin{array}{*{20}{c}} {{d_1} = \infty \Rightarrow {d_1}' = {f_1}} \\ {{d_2} = \infty \Rightarrow {d_2}' = {f_2}} \end{array}} ight.

    Ta có:

    \left\{ \begin{gathered} \tan \alpha = \frac{{{A_1}{B_1}}}{{{f_2}}} \hfill \\ \tan {\alpha _0} = \frac{{{A_2}{B_2}}}{{{f_1}}} \hfill \\ \end{gathered} ight. \Rightarrow {G_\infty } = \frac{{{f_1}}}{{{d_2}}}

    => Số bội giác của kính thiên văn khi ngắm chừng ở vô cực tỉ lệ thuận với tiêu cự của vật kính và tỉ lệ nghịch với tiêu cự của thị kính.

  • Câu 7: Thông hiểu
    Tính tiêu cự và vị trí của vât·

    Một vật AB đặt vuông góc với trục chính của một thấu kính cho ảnh cùng chiều, nhỏ hơn vật 2 lần, cách thấu kính 6cm. Tiêu cự của thấu kính và vị trí của vật để có ảnh nhỏ hơn vật 3 lần lượt là

    Hướng dẫn:

     Vật cho ảnh cùng chiều, nhỏ hơn vật 2 lần => Ảnh ảo và d' = -6cm

    Ta có:

    \left\{ \begin{gathered} \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \hfill \\ k = - \frac{{d'}}{d} = \frac{{f - d}}{f} = \frac{1}{2} \hfill \\ \end{gathered} ight. \Rightarrow f = \frac{{d'}}{{1 - k}} = - 12cm

  • Câu 8: Vận dụng
    Tính khoảng cách từ S' đến thấu kính

    Hai ngọn đèn S1 và S2 (coi như các điểm sáng) đặt cách nhau 16cm trên trục chính của thấu kính có tiêu cự 6cm. Ảnh tạo bởi thấu kính của S1 và S2 trùng nhau tạo S’ (hình vẽ). Khoảng cách từ S’ tới thấu kính là:

    Tính khoảng cách từ S' đến thấu kính

    Hướng dẫn:

    Ảnh của S1 và S2 trùng nhau nên thấu kính là thấu kính hội tụ và một trong hai ảnh là ảnh ảo, các đèn ở hai phía so với thấu kính.

    Giả sử S1 cho ảnh ảo

    => \left\{ \begin{gathered} {d_1} = {d_2} = a = 16cm \hfill \\ {d_2}\prime = - {d_1}\prime \hfill \\ \end{gathered} ight.

    Ta lại có:

    \begin{matrix} \left\{ \begin{gathered} \dfrac{1}{{{d_1}}} + \dfrac{1}{{{d_1}'}} = \dfrac{1}{{{f_1}}} \hfill \\ \dfrac{1}{{{d_2}}} + \dfrac{1}{{{d_2}'}} = \dfrac{1}{{{d_2}}} + \dfrac{1}{{ - {d_1}'}} = \dfrac{1}{{{f_2}}} \hfill \\ \end{gathered} ight. \hfill \\ \Leftrightarrow \dfrac{2}{f} = \dfrac{1}{{{d_1}}} + \dfrac{1}{{{d_2}}} \hfill \\ \Leftrightarrow \dfrac{2}{f} = \dfrac{1}{{{d_1}}} + \dfrac{1}{{a - {d_1}}} \hfill \\ \Leftrightarrow {d_1}^2 - a.{d_1} + \dfrac{a}{2}.f = 0 \hfill \\ \Rightarrow {d_1} = 4cm \Rightarrow {d_1}' = - 12cm \hfill \\ \end{matrix}

     

  • Câu 9: Vận dụng
    Tính tiêu cự f

    Một vật sáng AB đặt trước và vuông góc với trục chính của thấu kính ảnh A1B1 cùng chiều với vật. Dịch vật ra xa thấu kính thêm 3cm ta được ảnh A2B2 = 2A1B1, ảnh A2B2 vẫn cùng chiều với vật và dịch đi so với ảnh trước 24cm. Tiêu cự của thấu kính này là

    Hướng dẫn:

    Từ công thức thấu kính và số phòng đại ta có: \left\{ \begin{gathered} d' = f.\left( {1 - k} ight) \hfill \\ d = f.\left( {1 - \frac{1}{k}} ight) \hfill \\ \end{gathered} ight.

    Ta có:

    \frac{{{A_2}{B_2}}}{{{A_1}{B_1}}} = \frac{{{A_2}{B_2}}}{{AB}}.\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{k_2}}}{{{k_1}}} = 2 (*)

    Tỉ lệ độ dịch chuyển ảnh và độ dịch chuyển vật:

    \begin{matrix} \left| {\dfrac{{\Delta d}}{{\Delta d'}}} ight| = \left| {\dfrac{{{d_2} - {d_1}}}{{{d_2}' - {d_1}'}}} ight| = \left| {\dfrac{{\dfrac{1}{{{k_1}}} - \dfrac{1}{{{k_2}}}}}{{{k_1} - {k_2}}}} ight| \hfill \\ = \left| {\dfrac{{ - 1}}{{{k_1}.{k_2}}}} ight| = \dfrac{3}{{24}} = \dfrac{1}{8} \hfill \\ \Rightarrow \left| {{k_1}.{k_2}} ight| = 8 \hfill \\ \end{matrix}

    Vì ảnh luôn cùng chiều với vật nên:

    {k_1}.{k_2} > 0 \Rightarrow {k_1}.{k_2} = 8\left( {**} ight)

    Từ (*) và (**) => {k_1} = 2;{k_2} = 4

    Mặt khác \Delta d = f.\left( {\frac{1}{{{k_1}}} - \frac{1}{{{k_2}}}} ight) \Rightarrow f = 12cm > 0

    Vì f > 0 nên đây là thấu kính hội tụ.

  • Câu 10: Vận dụng
    Tính tiêu cự

    Một vật sáng AB đặt vuông góc với trục chính của thấu kính cho ảnh thật. Nếu cho vật dịch chuyển lại gần thấu kính 30cm thì ảnh sau của AB vẫn là ảnh thật nằm cách vật một khoảng như cũ và cao gắp 4 lần ảnh trước. Tiêu cự của thấu kính này là

    Hướng dẫn:

     Ảnh trước và sau di chuyển đều là ảnh thật

    => \frac{{{A_2}{B_2}}}{{{A_1}{B_1}}} = \frac{{{A_2}{B_2}}}{{AB}}.\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{k_2}}}{{{k_1}}} = 4\left( * ight)

    Theo công thức thấu kính và số phòng đại ta có: \left\{ \begin{gathered} d' = f.\left( {1 - k} ight) \hfill \\ d = f.\left( {1 - \frac{1}{k}} ight) \hfill \\ \end{gathered} ight.

    => Độ dịch chuyển của vật là: 

    \Delta d = {d_2} - {d_1} = f\left( {\frac{1}{{{k_1}}} - \frac{1}{{{k_2}}}} ight) = - 30

    Sau khi di chuyển vật lại gần, ảnh cách vật một khoảng như cũ nên ảnh di chuyển ra xa thêm đoạn 30cm.

    Độ dịch chuyển ảnh:

    \Delta d' = {d_2}' - {d_1}' = f\left( {{k_1} - {k_2}} ight) = 30

    Tỉ lệ độ dịch chuyển ảnh và độ dịch chuyển vật:

    \dfrac{{\Delta d}}{{\Delta d'}} = \dfrac{{\dfrac{1}{{{k_1}}} - \dfrac{1}{{{k_2}}}}}{{{k_1} - {k_2}}} = - 1 \Rightarrow {k_1}{k_2} = 1\left( {**} ight)

    Ảnh thật => {k_1} < 0;{k_2} < 0

    Từ (*) và (**) => {k_1} = - \frac{1}{2};{k_2} = - 2 \Rightarrow f = 20\left( {cm} ight)

  • Câu 11: Thông hiểu
    Cách dịch chuyển vật

    Để được ảnh sau cao bằng vật thì phải dịch chuyển vật từ vị trí ban đầu một đoạn

    Hướng dẫn:

     Ta có: {d_1} = f\left( {1 - \frac{1}{{{k_1}}}} ight) = 60\left( {cm} ight)

    Để ảnh cao bằng vật thì {d_2} = 2.f = 40\left( {cm} ight)

    ⇒ Dịch vật lại gần thấu kính 20cm.

  • Câu 12: Vận dụng
    Khoảng cách từ màn đến thấu kính

    Một thấu kính hội tụ có tiêu cự 10cm, có dạng hình tròn. Điểm sáng đặt ở trục chính và trước thấu kính thì tìm được hai vị trí sao trên màn ảnh đặt sau thấu kính thu được vệt sáng tròn cùng đường kính rìa với thấu kính. Biết khoảng cách hai vị trí đặt vật cách nhau 10cm. Khoảng cách từ màn đến thấu kính là

    Hướng dẫn:

     Để thu được vệt sáng tròn có cùng đường kính đường rìa với thấu kính thì điểm sáng phải đặt tại tiêu điểm chính của thấu kính và vị trí thứ hai cách xa thấu kính hơn tiêu điểm chính 10cm

    Ảnh của S2 là điểm sáng S'2 nằm chính giữa màn với thấu kính.

    Ta có:

    \begin{matrix} \left\{ \begin{gathered} {d_1} = f = 10cm \hfill \\ {d_2} = f + 10 = 20cm \hfill \\ \end{gathered} ight. \hfill \\ \Rightarrow {d_2}' = \dfrac{{{d_2}.f}}{{{d_2} - f}} = 20\left( {cm} ight) \hfill \\ \end{matrix}

    Khoảng cách từ màn tới thấu kính là:

    2{d_2}' = 40\left( {cm} ight)

  • Câu 13: Vận dụng cao
    Tính khoảng thời gian nhỏ nhất

    Đặt điểm sáng S trên trục chính của thấu kính và cách thấu kính 11cm. Thu ảnh trên màn E được điểm sáng S’ đối xứng với S qua thấu kính. Nếu đặt mane tại điêu diện của thấu từ vị trí ban đầu dịch chuyển S ra xa thấu kính trên trục chính, S chuyển động nhanh dần đều với gia tốc 4m/s2 ( tốc độ ban đầu bằng 0). Khoảng thời gian nhỏ nhất để diện tích vệt sáng trên màn bằng 1/36 diện tích ban đầu là:

    Hướng dẫn:

    Tính khoảng thời gian nhỏ nhất

    Tính khoảng thời gian nhỏ nhất

    Tính khoảng thời gian nhỏ nhất

  • Câu 14: Vận dụng cao
    Tính đường kính cực tiểu của vết sáng

    Đặt điểm sáng S cách màn ảnh E một khoảng 100cm. Giữa S và màn đặt một thấu kính hội tụ có tiêu cự 36cm. Tịnh tiến thấu kính giữa điểm sáng S và màn có vị trí của thấu kính sao cho đường kính của vết sáng trên màn là nhỏ nhất. Biết đường kính đường rìa của thấu kính là 9cm. Đường kính cực tiểu của vết sáng là:

    Hướng dẫn: Theo bài ra, khoảng cách từ vật đến màn L = 100cm < 4f nên ảnh luôn nằm sau màn 
    Tính đường kính cực tiểu của vết sáng
  • Câu 15: Vận dụng
    Tính tiêu cự f

    Chiếu một chùm sáng hội tụ qua một lỗ tròn trên một màn chắn sáng, thấy chum sáng hội tụ tại một điểm trên đường thẳng vuông góc với mặt phẳng của lỗ và đi qua tâm lỗ tròn, cách tâm lỗ tròn một khoảng 10cm. Đặt vào lỗ tròn một thấu kính phân kì thì thấy chùm sáng hội tụ tại một điểm cách tâm lỗ tròn một khoảng 20cm. Tiêu cự của thấu kính là

    Hướng dẫn:

    Khi đặt thấu kính phân kì chắn lỗ tròn thì vật ban đầu là vật ảo, thu được ảnh thật nên ta có: d= -10cm; d’=20cm

    Theo công thức thấu kính: f=(d' d)/(d'+d)= -20cm

  • Câu 16: Vận dụng
    Tính khoảng cách từ vật tới vật kính

    Một kính hiển vi có vật kính với tiêu cự 4mm, thị kính với tiêu cự 20mm và độ dài quang học bằng 156mm. Người quan sát có mắt bình thường với điểm cực cận cách mắt một khoảng 25cm. Mắt đặt tại tiêu điểm ảnh của thị kính. Khoảng cách từ vật tới vật kính khi ngắm chừng ở điểm cực cận là

    Hướng dẫn:

     Theo bài ra: f_1 = 4mm;f_2 = 20mm;δ = 156mm và Đ =25 cm

    Khi ngắm chừng ở vô cực thì ảnh của vật qua vật kính tại tiêu diện của thị kính:

    \begin{matrix} {d_1}' = \delta + {f_1} = 16cm \hfill \\ \Rightarrow {d_1} = \dfrac{{{d_1}'.{f_1}}}{{{d_1}' - {f_1}}} = 4,102256mm \hfill \\ \end{matrix}

  • Câu 17: Thông hiểu
    Xác định loại kính và tính độ tụ

    Một người mắt cận thị có điểm cực cận cách mắt 11cm và điểm cực viễn cách mắt 51cm. Để sửa tật cận thị mắt phải đeo kính gì, có độ tụ bằng bao nhiêu? Biết rằng kính đeo cách mắt 1cm.

    Hướng dẫn:

    Mắt cận đeo kính phân kì:

    \begin{matrix} {f_k} = O{O_k} - O{C_v} = 1 - 51 = - 50\left( {cm} ight) \hfill \\ \Rightarrow D = \dfrac{1}{{ - 0,5}} = - 2dp \hfill \\ \end{matrix}

  • Câu 18: Thông hiểu
    Tính khoảng đặt vật

    Một người cận thị có khoảng nhìn rõ từ 10cm đến 40cm, quan sát một vật nhỏ qua kính lúp có độ tụ +10dp. Mắt đặt sát sau kính. Muốn nhìn rõ ảnh của vật qua lăng kính ta phải đặt vật trước kính và cách kính trong khoảng từ

    Hướng dẫn:

     Khi quan sát một vật nhỏ qua kính lúp, ảnh của vật phải nằm trong khoảng nhìn rõ của mắt. Mắt sát sau kính.

    Vật nằm tại CC(mới) qua kính cho ảnh ảo tại CC, áp dụng công thức thấu kính:

    \begin{matrix} \dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \hfill \\ f = 10\left( {cm} ight);d' = - 10\left( {cm} ight) \hfill \\ \Rightarrow d = 5\left( {cm} ight) \hfill \\ \end{matrix}

    Vật nằm tại CV(mới) qua kính cho ảnh ảo tại CV, áp dụng công thức thấu kính:

    \begin{matrix} \dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \hfill \\ f = 10\left( {cm} ight);d' = - 40\left( {cm} ight) \hfill \\ \Rightarrow d = 8\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 19: Thông hiểu
    Số bội giác của kính thiên văn

    Một kính thiên văn có vật kính với độ tụ 0,5dp. Thị kính cho phép nhìn vật cao 1mm đặt tong tiêu diện vật dưới góc là 0,05 rad. Số bội giác của kính thiên văn khi ngắm chừng ở vô cực là

    Hướng dẫn:

     Ta có:

    \begin{matrix} {f_1} = \dfrac{1}{D} = 2m = 200\left( {cm} ight) \hfill \\ {f_2} = \dfrac{{{A_1}{B_1}}}{{\tan \alpha }} = 20mm = 2\left( {cm} ight) \hfill \\ \end{matrix}

    Kính thiên văn cho ảnh tại tiêu diện của vật kính và thị kính

    => Số bội giác của kính khi ngắm chừng ở vô cực là {G_\infty } = \frac{{{f_1}}}{{{f_2}}} = 100

0/19
19 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (26%):
    2/3
  • Thông hiểu (32%):
    2/3
  • Vận dụng (32%):
    2/3
  • Vận dụng cao (11%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 456 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Vật Lí 11 (sách cũ)

Đăng nhập