Lớp 12 Toán 12 - Chân trời sáng tạo

Luyện tập Tích phân CTST

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tìm kết luận đúng

    Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) - F(1) bằng:

    Hướng dẫn:

    Theo định nghĩa tích phân ta có:

    \int_{0}^{1}{f(x)dx} = F(1) - F(0) suy ra F(0) - F(1) = - \int_{0}^{1}{f(x)dx}.

  • Câu 2: Thông hiểu
    Tính thời gian đi đến trường

    Một học sinh đi học từ nhà đến trường bằng xe đạp với vận tốc thay đổi theo thời gian được tính bởi công thức v(t) = 40t + 100(m/p). Biết rằng sau khi đi được 1 phút thì quãng đường học sinh đó đi được là 120m. Biết quãng đường từ nhà đến trường là 3km. Hỏi thời gian học sinh đó đi đến trường là bao nhiêu phút?

    Hướng dẫn:

    Ta có: S(t) = \int_{}^{}{v(t)dt} = 20t^{2} + 100t + C

    Vì S(1) = 120 + C = 120 \Rightarrow C = 0

    Để học sinh đó đến trường thì S(t) = 20t^{2} + 100t = 3000 \Leftrightarrow t = 10

    Vậy đáp án cần tìm là 10 phút.

  • Câu 3: Vận dụng cao
    Tính giá trị nhỏ nhất của tích phân

    Cho hàm số y = f(x) có đạo hàm và liên tục trên đoạn \lbrack a;bbrack với f(a) = 0. Đặt M = \max_{\lbrack a;bbrack}\left| f(x) ight|. Tìm giá trị nhỏ nhất của \int_{a}^{b}{\left\lbrack f'(x) ightbrack^{2}dx}?

    Hướng dẫn:

    Gọi x_{0} \in \lbrack a;bbrack sao cho \left| f\left( x_{0} ight) ight| = M. Ta có:

    \left( \int_{a}^{x_{0}}{f'(x)dx} ight)^{2} \leq \int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}.\int_{a}^{x_{0}}{dx}

    \Leftrightarrow \left\lbrack f\left( x_{0} ight) - f(a) ightbrack^{2} \leq \left( x_{0} - a ight)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}

    \Leftrightarrow f^{2}\left( x_{0} ight) \leq \left( x_{0} - a ight)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}

    \Leftrightarrow M^{2} \leq \left( x_{0} - a ight)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}

    Mà \left( x_{0} - a ight)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx} \leq (b - a)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}

    Suy ra M^{2} \leq (b - a)\int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx}

    \Rightarrow \int_{a}^{x_{0}}{\left\lbrack f'(x) ightbrack^{2}dx} \geq \frac{M^{2}}{b - a}

    Dấu bằng xảy ra khi và chỉ khi f'(x) = 1 .

    Vậy giá trị nhỏ nhất của \int_{a}^{b}{\left\lbrack f'(x) ightbrack^{2}dx} đạt được bằng \frac{M^{2}}{b - a} khi f'(x) = 1.

  • Câu 4: Thông hiểu
    Tính vận tốc của khinh khí cầu

    Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162m so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật v(t) = 10t - t^{2}, trong đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là:

    Hướng dẫn:

    Khi bắt đầu tiếp đất vật chuyển động được quãng đường làs = 162m

    Ta có: S = \int_{0}^{t_{0}}{\left( 10t - t^{2} ight)dt} = \left. \ \left( 5t - \frac{t^{3}}{3} ight) ight|_{0}^{t_{0}} = 5{t_{0}}^{2} - \frac{{t_{0}}^{3}}{3} (với t_{0} là thời điểm vật tiếp đất)

    Cho 5{t_{0}}^{2} - \frac{{t_{0}}^{3}}{3} = 162 \Leftrightarrow t_{0} = 9 (Do v(t) = 10t - t^{2} \Rightarrow 0 \leq t \leq 10)

    Khi đó vận tốc của vật là: v(9) = 10.9 - 9^{2} = 9(m/p).

  • Câu 5: Thông hiểu
    Xác định giá trị tích phân

    Cho hàm số y = f(x) có đạo hàm liên tục trên \mathbb{R} và có đồ thị như hình vẽ:

    Tích phân

    Tính tích phân I = \int_{1}^{2}{f'(2x - 1)dx}?

    Hướng dẫn:

    Ta có:

    I = \int_{1}^{2}{f'(2x - 1)dx} = \frac{1}{2}\int_{1}^{2}{f'(2x - 1)d(2x - 1)}

    = \frac{1}{2}\left. \ f(2x - 1)ight|_{1}^{2} = \frac{1}{2}\left\lbrack f(3) - f(1) ightbrack =2

  • Câu 6: Thông hiểu
    Tìm khẳng định đúng

    Chọn khẳng định đúng trong các khẳng định sau?

    Hướng dẫn:

    Đặt t = 1 - x \Rightarrow dt = - dx. Đổi cận \left\{ \begin{matrix} x = 0 \Rightarrow t = 1 \\ x = 1 \Rightarrow t = 0 \\ \end{matrix} ight.

    Ta có: \int_{0}^{1}{\sin(1 - x)dx} = - \int_{1}^{0}{\sin tdt} = \int_{0}^{1}{\sin xdx}.

    Vậy khẳng định đúng \int_{0}^{1}{\sin(1 - x)dx} = \int_{0}^{1}{\sin xdx}.

  • Câu 7: Nhận biết
    Xác định quãng đường vật chuyển động

    Một vật chuyển động chậm dần đều với vận tốc v(t) = 30 - 2t(m/s). Hỏi trong 5s trước khi dừng hẳn, vật di chuyển động được bao nhiêu mét?

    Hướng dẫn:

    Khi dừng hẳn v(t) = 30 - 2t = 0 \Rightarrow t = 15(s)

    Khi đó trong 5s trước khi dừng hẳn vật di chuyển được:

    S = \int_{10}^{15}{v(t)dt} = \int_{10}^{15}{(30 - 2t)dt} = 25m.

  • Câu 8: Nhận biết
    Chọn mệnh đề sai

    Giả sử f(x);g(x) là các hàm số bất kì liên tục trên \mathbb{R} và a;b;c là các số thực. Mệnh đề nào sau đây sai?

    Hướng dẫn:

    Theo tính chất tích phân ta có:

    \int_{a}^{b}{f(x)dx} + \int_{b}^{c}{f(x)dx} + \int_{c}^{a}{f(x)dx}

    = \int_{a}^{b}{f(x)dx} + \int_{b}^{c}{f(x)dx} - \int_{a}^{c}{f(x)dx}

    = \int_{a}^{c}{f(x)dx} - \int_{a}^{c}{f(x)dx} = 0

    \int_{a}^{b}{c.f(x)dx} = c.\int_{a}^{b}{f(x)dx};\forall x\mathbb{\in R}

    \int_{a}^{b}{\left\lbrack f(x) - g(x) ightbrack dx} + \int_{a}^{b}{g(x)dx}

    = \int_{a}^{b}{f(x)dx} - \int_{a}^{b}{g(x)dx} + \int_{a}^{b}{g(x)dx}

    = \int_{a}^{b}{f(x)dx}

    Vậy mệnh đề sai: \int_{a}^{b}{\left\lbrack f(x)g(x) ightbrack dx} = \int_{a}^{b}{f(x)dx}.\int_{a}^{b}{g(x)dx}

  • Câu 9: Thông hiểu
    Tính tích phân K

    Cho hàm số f(x);g(x) là các hàm số liên tục trên \lbrack 1;3brack và thỏa mãn \int_{1}^{3}{\left\lbrack f(x) + 3g(x) ightbrack dx} = 10 và \int_{1}^{3}{\left\lbrack 2f(x) - g(x) ightbrack dx} = 6. Tính tích phân K = \int_{1}^{3}{\left\lbrack f(x) + g(x) ightbrack dx}?

    Hướng dẫn:

    Theo bài ra ta có:

    \left\{ \begin{matrix}\int_{1}^{3}{\left\lbrack f(x) + 3g(x) ightbrack dx} = 10 \\\int_{1}^{3}{\left\lbrack 2f(x) - g(x) ightbrack dx} = 6 \\\end{matrix} ight.\Leftrightarrow \left\{ \begin{matrix}\int_{1}^{3}{f(x)dx} + 3\int_{1}^{3}{g(x)dx} = 10 \\2\int_{1}^{3}{f(x)dx} - \int_{1}^{3}{g(x)dx} = 6 \\\end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}\int_{1}^{3}{f(x)dx} = 4 \\\int_{1}^{3}{g(x)dx} = 2 \\\end{matrix} ight.\Rightarrow K = \int_{1}^{3}{\left\lbrack f(x) +g(x) ightbrack dx} = 4.2 = 6

  • Câu 10: Nhận biết
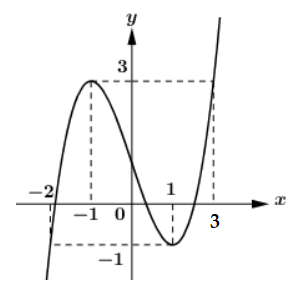
    Tìm tích phân

    Cho hàm số f(x) liên tục trên tập số thực và thỏa mãn \int_{0}^{6}{f(x)dx}= 7;\int_{3}^{10}{f(x)dx} = 8;\int_{3}^{6}{f(x)dx} = 9. Khi đó giá trị I = \int_{0}^{10}{f(x)dx} bằng:

    Hướng dẫn:

    Ta có:

    \int_{3}^{10}{f(x)dx} = \int_{3}^{6}{f(x)dx} + \int_{6}^{10}{f(x)dx}

    \Leftrightarrow \int_{6}^{10}{f(x)dx} = \int_{3}^{6}{f(x)dx} - \int_{3}^{10}{f(x)dx} = 8 - 9 = 1

    \Rightarrow I = \int_{0}^{6}{f(x)dx} + \int_{6}^{10}{f(x)dx} = 7 - 1 = 6

  • Câu 11: Thông hiểu
    Tìm các giá trị thực của tham số m

    Tìm tất cả các giá trị thực của tham số m thỏa mãn \int_{0}^{m}{(2x + 1)dx} < 2?

    Hướng dẫn:

    Ta có: \int_{0}^{m}{(2x + 1)dx} < 2 \Leftrightarrow \left. \ \left( x^{2} + x ight) ight|_{0}^{m} < 2

    \Leftrightarrow m^{2} + m - 2 < 0 \Leftrightarrow - 2 < m < 1

  • Câu 12: Vận dụng
    Tính tích phân

    Cho hàm số f(x) đồng biến và có đạo hàm cấp hai trên đoạn \lbrack 0;2brack và thỏa mãn 2\left\lbrack f(x) ightbrack^{2} - f(x).f''(x) + \left\lbrack f'(x) ightbrack^{2} = 0 với \forall x \in \lbrack 0;2brack. Biết rằng f(0) = 1;f(2) = e^{6} khi đó tích phân M = \int_{- 2}^{0}{(2x + 1)f(x)dx} bằng:

    Hướng dẫn:

    Ta có:

    2\left\lbrack f(x) ightbrack^{2} - f(x).f''(x) + \left\lbrack f'(x) ightbrack^{2} = 0

    \Leftrightarrow f(x).f''(x) - \left\lbrack f'(x) ightbrack^{2} = 2\left\lbrack f(x) ightbrack^{2}

    \Leftrightarrow \frac{f(x).f''(x) - \left\lbrack f'(x) ightbrack^{2}}{\left\lbrack f(x) ightbrack^{2}} = 2

    \Leftrightarrow \left\lbrack \frac{f'(x)}{f(x)} ightbrack' = 2 \Leftrightarrow \int_{}^{}{\left\lbrack \frac{f'(x)}{f(x)} ightbrack'dx} = \int_{}^{}{2dx}

    \Leftrightarrow \frac{f'(x)}{f(x)} = 2x + C_{1} \Leftrightarrow \ln\left| f(x) ight| = x^{2} + C_{1}x + C_{2}

    Theo bài ra ta có:

    \left\{ \begin{matrix} f(0) = 1 \\ f(2) = e^{6} \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} ln1 = C_{2} \\ 4 + 2C_{1} = 6 \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} C_{2} = 0 \\ C_{1} = 1 \\ \end{matrix} ight.

    \Rightarrow \ln\left| f(x) ight| = x^{2} + x \Rightarrow f(x) = e^{x^{2} + x}

    \Rightarrow M = \int_{- 2}^{0}{(2x + 1)e^{x^{2} + x}dx} = \left. \ e^{x^{2} + x} ight|_{- 2}^{0} = 1 - e^{2}

  • Câu 13: Thông hiểu
    Tính giá trị biểu thức

    Cho \int_{0}^{1}{\frac{x}{(x + 2)^{2}}dx} = a + ln2 + cln3 với a;b;c là các số hữu tỉ. Giá trị của biểu thức K = 3a + b + c bằng:

    Hướng dẫn:

    Ta có: \int_{0}^{1}{\frac{x}{(x + 2)^{2}}dx} = \int_{0}^{1}{\frac{x + 2 - 2}{(x + 2)^{2}}dx}

    = \int_{0}^{1}{\frac{x + 2}{(x + 2)^{2}}dx} - \int_{0}^{1}{\frac{2}{(x + 2)^{2}}dx}

    = \int_{0}^{1}{\frac{1}{x + 2}dx} - \int_{0}^{1}{\frac{2}{(x + 2)^{2}}dx}

    = \left. \ \ln|x + 2| ight|_{0}^{1} -\left. \ \frac{2}{x + 2} ight|_{0}^{1} = \ln3 - \ln2 -\frac{1}{3}

    Suy ra a = - \frac{1}{3};b = - 1;c = 1 \Rightarrow K = - 1

  • Câu 14: Vận dụng
    Tính tổng các giá trị tham số m

    Tổng tất cả các giá trị của tham số m thỏa mãn \int_{0}^{1}{\frac{9^{x} + 3m}{9^{x} + 3}dx} = m^{2} - 1 bằng:

    Hướng dẫn:

    Ta có:

    \int_{0}^{1}{\frac{9^{x} + 3m}{9^{x} + 3}dx} = m^{2} - 1

    \Leftrightarrow \int_{0}^{1}{\frac{9^{x}}{9^{x} + 3}dx} + m\int_{0}^{1}{\frac{3}{9^{x} + 3}dx} = m^{2} - 1

    \Leftrightarrow m^{2} - m\int_{0}^{1}{\frac{3}{9^{x} + 3}dx} - \int_{0}^{1}{\frac{9^{x}}{9^{x} + 3}dx} - 1 = 0

    Phương trình trên là phương trình bậc hai đối với biến m, với các hệ số
    \left\{ \begin{matrix}a = 1 \\b = - \int_{0}^{1}{\dfrac{3}{9^{x} + 3}dx} \\c = - \int_{0}^{1}{\dfrac{9^{x}}{9^{x} + 3}dx} \\\end{matrix} ight..

    Áp dụng hệ thứ Vi- et \Rightarrow m_{1} + m_{2} = \frac{- b}{a} = \int_{0}^{1}{\frac{3}{9^{x} + 3}dx} = \frac{1}{2}

  • Câu 15: Thông hiểu
    Xác định tích phân

    Tính tích phân B = \int_{0}^{2}{2x\left( x^{2} + 1 ight)^{2018}dx}?

    Hướng dẫn:

    Ta có: B = \int_{0}^{2}{2x\left( x^{2} + 1 ight)^{2018}dx}

    = \int_{0}^{2}{\left( x^{2} + 1 ight)^{2018}d\left( x^{2} + 1 ight)}

    = \left. \ \frac{\left( x^{2} + 1 ight)^{2019}}{2019} ight|_{0}^{2} = \frac{5^{2019} - 1}{2019}

  • Câu 16: Vận dụng cao
    Tính tích phân I

    Cho hàm số f(x) liên tục trên đoạn \lbrack - 6;5brack có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ:

    Tính giá trị I = \int_{- 6}^{5}{\left\lbrack f(x) + 2 ightbrack dx}?

    Hướng dẫn:

    Hình vẽ minh họa

    Dựa vào đồ thị ta có: A( - 6; - 1),B( - 2;1) suy ra phương trình đường thẳng AB:y = \frac{1}{2}x + 2

    \Rightarrow I_{1} = \int_{0}^{- 2}{\left\lbrack \frac{1}{2}x + 2 + 2 ightbrack dx} = 8

    Phương trình đường tròn (C): x^{2} + (y - 1)^{2} = 4 \Rightarrow y = 1 + \sqrt{4 - x^{2}}

    \Rightarrow I_{2} = \int_{- 2}^{2}{\left\lbrack 1 + \sqrt{4 - x^{2}} + 2 ightbrack dx} = 12 + 2\pi

    Điểm C(2;1),D(5;3) nên phương trình đường thẳng CD là: y = \frac{2}{3}x - \frac{1}{3}

    \Rightarrow I_{3} = \int_{2}^{5}{\left\lbrack \frac{2}{3}x - \frac{1}{3} + 2 ightbrack dx} = 12

    Vậy I = I_{1} + I_{2} + I_{3} = 32 + 2\pi

  • Câu 17: Nhận biết
    Tính tích phân

    Tính tích phân I =\int_{0}^{\frac{\pi}{2}}{\left( \sin2x + \sin x ight)dx}?

    Hướng dẫn:

    Ta có:

    I = \int_{0}^{\frac{\pi}{2}}{\left(\sin2x + \sin x ight)dx} = \left. \ \left( - \frac{1}{2}\cos2x - \cos xight) ight|_{0}^{\frac{\pi}{2}} = 2

  • Câu 18: Nhận biết
    Tính tích phân

    Tích phân I = \int_{0}^{1}{3^{x}dx} bằng:

    Hướng dẫn:

    Ta có:

    I = \int_{0}^{1}{3^{x}dx} = \left. \frac{3^{x}}{\ln3} ight|_{0}^{1} = \frac{2}{\ln3}

  • Câu 19: Nhận biết
    Tính tích phân

    Cho \int_{- 1}^{2}{f(x)dx} = 2 và \int_{- 1}^{2}{g(x)dx} = - 1, khi đó \int_{- 1}^{2}{\left\lbrack x + 2f(x) + 3g(x) ightbrack dx} bằng:

    Hướng dẫn:

    Ta có:

    \int_{- 1}^{2}{\left\lbrack x + 2f(x) + 3g(x) ightbrack dx} = \int_{- 1}^{2}{xdx} + 2\int_{- 1}^{2}{f(x)dx} + 3\int_{- 1}^{2}{g(x)dx}

    = \left. \ \frac{1}{2}x^{2} ight|_{- 1}^{2} + 2.2 + 3.( - 1) = \frac{5}{2}

  • Câu 20: Thông hiểu
    Tính tích phân

    Giá trị của H = \int_{0}^{1}{\left( \frac{1}{2x + 1} + 3\sqrt{x} ight)dx}?

    Hướng dẫn:

    Ta có:

    H = \int_{0}^{1}{\left( \frac{1}{2x + 1} + 3\sqrt{x} ight)dx} = \left. \ \left( \frac{1}{2}\ln|2x + 1| + 2x^{\frac{3}{2}} ight) ight|_{0}^{1} = 2 + \ln\sqrt{3}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (35%):
    2/3
  • Thông hiểu (45%):
    2/3
  • Vận dụng (10%):
    2/3
  • Vận dụng cao (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 2 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12 CTST

Đăng nhập