Cho hình vẽ, khẳng định nào sau đây là đúng?
Ta có
Mà hai góc này ở vị trí so le trong nên AB // CD
Phát biểu nào dưới đây là đúng:
Phát biểu đúng: “Hai đường thẳng song song có cặp góc so le trong, đồng vị bằng nhau, trong cùng phía bù nhau”.
Cho hình vẽ:
Biết . Tính số đo góc ?
Ta có:
và
là hai góc đồng vị
Suy ra
Cho hình vẽ. Biết a // b. Khi đó kết luận nào sau đây là không đúng?
Vì a // b nên
(Hai góc đồng vị)
(Hai góc đối đỉnh) mà
(Hai góc đồng vị)
(Hai góc đồng vị)
(Hai góc kề bù)
Vậy đáp án sai là: .
Cho hình vẽ sau, biết . Số đo của bằng bao nhiêu?
Ta có: nên hai góc trong cùng phía bù nhau
Suy ra .
Cho hình vẽ sau:
Biết . là đường phân giác của . Tia phân giác của góc cắt tại . Qua kẻ đường thẳng song song với cắt và lần lượt tại và .
a) Số đo góc bằng 35
b) Số đó góc bằng: 70
Cho hình vẽ sau:
Biết .
là đường phân giác của
. Tia phân giác của góc
cắt
tại
. Qua
kẻ đường thẳng song song với
cắt
và
lần lượt tại
và
.
a) Số đo góc bằng 35
b) Số đó góc bằng: 70
a) Ta có là tia phân giác của
.
Mà nên
b) Ta có (hai góc trong cùng phía).
Mà (GT) nên
Ta có (hai góc đồng vị).
Mà nên
Cho hình vẽ, khẳng định nào sau đây là sai?
Ta có AM cắt BC tại C nên AM không song song với BC.
Cho hai đường thẳng và cắt đường thẳng tại và , số đo . Xác định số đo của góc để ?
Để thì hai góc đồng vị bằng nhau, suy ra
Trong các câu sau có bao nhiêu câu đúng? Nếu một đường thẳng cắt nhau hai đường thẳng song song thì
(1) Hai góc đồng vị bằng nhau.
(2) Hai góc so le ngoài bằng nhau.
(3) Hai góc trong cùng phía bằng nhau.
(4) Hai góc so le trong bằng nhau.
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong còn lại bằng nhau, hai góc so le ngoài bằng nhau.
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Nên cả (1), (2), (3), (4) đều đúng.
Cho hình vẽ:
Biết a // b và . Tia là tia phân giác của góc . Tính ?
Ta có: a // b suy ra (Hai góc so le trong)
Mà
Ta lại có (Tia BD là tia phân giác của
)
Ta lại có (Hai góc so le trong)
Cho hình vẽ, biết AD; MN lần lượt là các tia phân giác của và , , khẳng định nào sau đây sai?
Ta có (vì
là phân giác của
và
)
là phần giác của
Suy ra mà
và
ở vị trí đồng vị nên
Cho hình vẽ. Khẳng định nào sau đây sai?
Ta có Ax cắt AB tại A nên Ax không thể song song với AB.
Cho và Tính
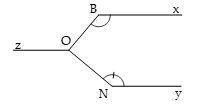
Đáp án: 90
Cho và
Tính
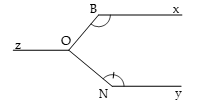
Đáp án: 90
Kẻ là tia đối của tia
.
Cho hình vẽ sau, biết . Số đo của bằng bao nhiêu?
Một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Ta có:
;
nằm ở vị trí so le trong.
Suy ra .
Cho hình vẽ bên với đôi một song song. Tính, số đo góc , biết và .
Ta có: Ax // By
= 45°
Lại có: Ct // By => = 45°.
Vậy .
Cho hình vẽ, kết luận nào sau đây là đúng?
Ta có:
MÀ là hai góc so le trong nên
Cho đường thẳng c cắt hai đường thẳng a b, và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì
Cho đường thẳng c cắt hai đường thẳng a b, và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Quan sát hình sau. Biết rằng . Khi đó vì là một cặp góc
Ta có:
Khi đó vì là một cặp góc đồng vị.
Cho hình vẽ, biết khẳng định nào sau đây là đúng?
Ta có:
Mà
Mà hai góc ở vị trí so le trong nên
.
Cho hình vẽ. Biết a // AO và a // b. Tính số đo góc ?
Ta có (GT) và
(GT).
Nên (cùng song song với
)
Ta có (GT)
(hai góc so le trong).
Mà nên
Ta có (hai góc so le trong).
Mà (GT) nên
Ta lại có (Tia
nằm giữa hai tia
)
