Lớp 9 Toán 9 - Cánh diều

Bài tập cuối chương 5 Đường tròn Cánh Diều

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tìm khẳng định chưa chính xác

    Cho tam giác MNP và hai đường cao MH;NK. Gọi (O) là đường tròn nhận MN là đường kính. Khẳng định nào sau đây không đúng?

    Hướng dẫn:

    Hình vẽ minh họa

    Ta suy ra khẳng định đúng là “Bốn điểm M,N,H,K không cùng nằm trên đường tròn (O).”

  • Câu 2: Nhận biết
    Chọn khẳng định sai

    Trong các khẳng định sau, khẳng định nào sai?

    Hướng dẫn:

    Khẳng định sai là: “Khi dây AB đi qua O thì dây AB là đường kính.”

  • Câu 3: Thông hiểu
    Tính độ dài cạnh AD

    Cho đường tròn (O;4cm). Vẽ dây cung AB = 5cm, điểm C trên dây cung AB sao cho AC = 2cm. Vẽ CD vuông góc với OA tại D. Tính độ dài đoạn AD?

    Hướng dẫn:

    Hình vẽ minh họa

    Vẽ đường kính AE có AE = 8cm

    Điểm B thuộc đường tròn đường kính AE

    \Rightarrow \widehat{ABE} = 90^{0}

    Xét tam giác ADC và tam giác ABE có:

    Góc A chung

    \widehat{ABE} = \widehat{ADC} = 90^{0}

    \Rightarrow \Delta ADC\sim\Delta ABE(g - g)

    \Rightarrow \frac{AD}{AB} = \frac{AC}{AE} \Rightarrow AD = \frac{AB.AC}{AE} = \frac{2.5}{8} = \frac{5}{4}(cm)

  • Câu 4: Thông hiểu
    Tìm độ dài OH

    Đường tròn (O;R) có hai bán kính OA;OB vuông góc với nhau. Gọi H là trung điểm của AB. Tính độ dài OH theo bán kính R?

    Hướng dẫn:

    Áp dụng định lí Pythagore cho tam giác vuông ta có:

    AB = \sqrt{OA^{2} + OB^{2}} = \sqrt{R^{2} + R^{2}} = R\sqrt{2}

    Vì H là trung điểm của AB nên OH = \frac{1}{2}AB = \frac{R\sqrt{2}}{2} (tính chất tam giác vuông)

  • Câu 5: Nhận biết
    Chọn đáp án đúng

    Cho đường tròn (O;7cm), đường thẳng d là tiếp tuyến của đường tròn (O;7cm). Khi đó:

    Hướng dẫn:

    Đường thẳng d là tiếp tuyến của đường tròn (O;7cm) do đó khoảng cách từ điểm O đến đường thẳng d bằng bán kính bằng 7cm.

  • Câu 6: Nhận biết
    Chọn khẳng định đúng

    Chọn khẳng định đúng trong các khẳng định dưới đây?

    Hướng dẫn:

    Theo định lí về dấu hiệu nhận biết tiếp tuyến của đường tròn ta có: “Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.”

  • Câu 7: Thông hiểu
    Chọn kết luận đúng

    Cho hình vuông ABCD, trên đường chéo BD lấy điểm I sao cho BI = BA. Đường thẳng I vuông góc với BD cắt AD tại E. Chọn kết luận đúng?

    Hướng dẫn:

    Hình vẽ minh họa:

    Ta có: \Delta AEB = \Delta IEB(ch - gn) \Rightarrow AE = EI

    \Rightarrow I \in (E;EA) \Rightarrow R = EI

    Mặt khác EI\bot BD \Rightarrow d = EI \Rightarrow d = R

    Suy ra đường thẳng BD tiếp xúc với (E;AE).

  • Câu 8: Thông hiểu
    Tính độ dài CD

    Cho nửa đường tròn (O;5cm) và đường thẳng d cắt đường tròn tại hai điểm CD và cách đường tròn một khoảng 3cm. Tính độ dài dây CD?

    Hướng dẫn:

    Hình vẽ minh họa

    Kẻ đường cao OH. Vì OH\bot CD và tam giác OCD cân tại O nên H là trung điểm của CD

    \Rightarrow HC = \sqrt{5^{2} - 3^{2}} = 4(cm)

    \Rightarrow CD = 2HC = 2.4 = 8cm

  • Câu 9: Vận dụng
    Tìm diện tích lớn nhất của ABCD

    Cho nửa đường tròn tâm O, đường kính AB = 10cm. Điểm M thuộc nửa đường tròn. Qua M kẻ tiếp tuyến xy với nửa đường tròn. Gọi D;C lần lượt là hình chiếu của A;B trên xy. Diện tích lớn nhất của tứ giác ABCD là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tứ giác ABCD là hình thang vuông, MO là đường trung bình của hình thang.

    \Rightarrow S_{ABCD} = \frac{CD.(AC + BD)}{2} = CD.OM

    \leq AB.OM = 2R^{2} = 50cm^{2}

    Suy ra diện tích ABCD đạt giá trị lớn nhất là 50cm^{2} khi CD//AB.

  • Câu 10: Vận dụng cao
    Tính diện tích tam giác OMN

    Cho đường tròn (O;R) và một dây cung AB = \frac{8R}{5} . Kẻ một tiếp tuyến song song với AB, cắt các tia OA;OB theo thứ tự tại M;N. Khi đó diện tích tam giác OMN bằng:

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có: (O;R) có MN là tiếp tuyến tại I \Rightarrow MN\bot OI tại I.

    Mà MN//AB nên OI\bot AB

    \Rightarrow BJ = AJ = \frac{AB}{2} = \frac{\frac{8R}{5}}{2} = \frac{4R}{5}

    Xét tam giác OBJ vuông tại J ta có:

    OB^{2} = BJ^{2} + OJ^{2}

    \Rightarrow OJ = \sqrt{OB^{2} - BJ^{2}} = \sqrt{R^{2} - \left( \frac{4R}{3} ight)^{2}} = \frac{3R}{5}

    \Rightarrow S_{OAB} = \frac{1}{2}OJ.AB = \frac{1}{2}.\frac{3}{5}R.\frac{8}{5}R = \frac{12}{25}R^{2}

    Tam giác OAB có MN // AB suy ra \Delta OAB\sim\Delta OMN

    \Rightarrow \left\{ \begin{matrix}\dfrac{AB}{MN} = \dfrac{OJ}{OI} = \dfrac{\dfrac{3R}{5}}{R} = \dfrac{3}{5} \\\dfrac{S_{OAB}}{S_{OMN}} = \left( \dfrac{AB}{MN} ight)^{2} \\\end{matrix} ight.

    \Rightarrow \frac{S_{OAB}}{S_{OMN}} = \left( \frac{3}{5} ight)^{2} = \frac{9}{25}

    \Rightarrow S_{OMN} = \frac{25}{9}.\frac{12}{25}R^{2} = \frac{4}{3}R^{2}

  • Câu 11: Nhận biết
    Hoàn thành khẳng định

    Chọn khẳng định đúng? Góc ở tâm là góc

    Hướng dẫn:

    Góc có đỉnh trùng với tâm của đường tròn gọi là góc ở tâm.

  • Câu 12: Nhận biết
    Chọn khẳng định đúng

    Chọn khẳng định đúng. Cho đường tròn (O) có cung MN < cung PQ, khi đó:

    Hướng dẫn:

    Cho đường tròn (O) có cung MN < cung PQ, khi đó MN < PQ.

  • Câu 13: Thông hiểu
    Tính số đo cung nhỏ AB

    Cho tam giác OAO' vuông cân tại A. Vẽ các đường tròn (O;OA) và (O';O'A) cắt nhau tại điểm B;(B eq A). Xác định số đo cung nhỏ AB?

    Hướng dẫn:

    Hình vẽ minh họa:

    Xét tam giác OAO’ và OBO’ có

    OB = OA

    O’B = O’A

    OO’ chung

    Suy ra \Delta OAO' = \Delta OBO'(c - c - c)

    \Rightarrow \widehat{BOO'} = \widehat{AOO'} = 45^{0} (vì tam giác OAO’ vuông cân tại A)

    Suy ra sd\widehat{AB} = \widehat{AOB} = 2\widehat{AOO'} = 2.45^{0} = 90^{0}

    Vậy số đo cung nhỏ AB bằng 90^{0}.

  • Câu 14: Thông hiểu
    Chọn đáp án đúng

    Quan sát hình vẽ:

    Biết rằng BC là đường kính và \widehat{AOD} = 45^{0};\widehat{COA} = 55^{0}. Tính số đo cung nhỏ BD và chọn kết luận đúng giữa hai cung nhỏ AB và CD?

    Hướng dẫn:

    Xét đường tròn (O) ta có:

    \widehat{COA} + \widehat{AOD} + \widehat{DOB} = 180^{0} (vì BC là đường kính)

    \Rightarrow \widehat{DOB} = 180^{0} - \left( \widehat{COA} + \widehat{AOD} ight) = 80^{0}

    Suy ra số đo cung nhỏ BD là: \widehat{DOB} = 80^{0}

    Số đo cung nhỏ AD là: \widehat{AOD} = 45^{0}

    Số đo cung nhỏ AC là \widehat{AOC} = 55^{0}

    sd\widehat{AB} nhỏ = sd\widehat{AD} nhỏ + sd\widehat{BD} nhỏ = 45^{0} + 80^{0} = 125^{0}

    sd\widehat{CD} nhỏ = sd\widehat{CA} nhỏ + sd\widehat{AD} nhỏ = 55^{0} + 45^{0} = 100^{0}

    Suy ra hai cung nhỏ cần tìm có mối quan hệ là sd\widehat{AB} > sd\widehat{CD}.

    Vậy đáp án chính xác nhất là: sd\widehat{BD} = 80^{0};sd\widehat{AB} > sd\widehat{CD}

  • Câu 15: Vận dụng
    Chọn khẳng định đúng

    Cho đường tròn (O;R) và điểm P sao cho OP = 2R. Đường tròn tâm I đường kính OP cắt đường tròn (O) tại A;B. Chọn khẳng định đúng trong các khẳng định dưới đây?

    Hướng dẫn:

    Hình vẽ minh họa:

    Vì I là tâm đường tròn đường kính OP = 2R

    \Rightarrow OI = IP = \frac{OP}{2} = R

    Vậy I là điểm thuộc đường tròn (O; R)

    Theo tính chất của hai tiếp tuyến cắt nhau ta có:

    \widehat{O_{1}} = \widehat{O_{2}} = \frac{1}{2}\widehat{AOB}

    Mà \cos\widehat{O_{1}} = \frac{OA}{OP} = \frac{R}{2R} = \frac{1}{2} \Rightarrow \widehat{O_{1}} = 60^{0}

    \Rightarrow \widehat{AOB} = 2.60^{0} = 120^{0}

    \Rightarrow sd\widehat{AB} = \widehat{AOB} = 120^{0}

    Tam giác PAO vuông tại A ta có:

    \widehat{O_{1}} = 60^{0} \Rightarrow \widehat{OPA} = 30^{0}

    \Rightarrow \widehat{APB} = 2.30^{0} = 60^{0}

    Vậy khẳng định đúng là: “Điểm I thuộc đường tròn (O).”

  • Câu 16: Nhận biết
    Chọn đẳng thức sai

    Cho hình vẽ:

    Đẳng thức nào sau đây sai?

    Hướng dẫn:

    Ta có:

    \widehat{BEC} = \frac{1}{2}\widehat{BOC} sai vì \widehat{BEC} không phải góc nội tiếp chắn cung BnC.

  • Câu 17: Nhận biết
    Xác định khẳng định sai

    Cho các khẳng định sau, xác định khẳng định sai?

    Hướng dẫn:

    Góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.

    Vậy khẳng định sai là: “Góc có đỉnh nằm trong đường tròn được gọi là góc ở tâm”

  • Câu 18: Thông hiểu
    Tính đường kính của đường tròn (O)

    Cho tam giác ABC nội tiếp đường tròn (O; R), đường cao AH, biết AB = 12cm, AC = 15cm, AH = 6cm. Tính đường kính của đường tròn (O).

    Hướng dẫn:

    Hình vẽ minh họa

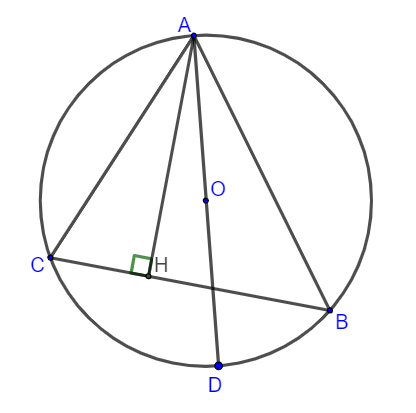
    Tính đường kính của đường tròn (O)

    Kẻ đường kính AD.

    \widehat {ACB} = \widehat {ADB} (hai góc nội tiếp cùng chắn cung AB)

    \widehat {ABD} =90^0 (góc nội tiếp chắn nửa đường tròn)

    Xét tam giác ACH và tam giác ADB có:

     \widehat {ACB} = \widehat {ADB}

    \widehat {AHC}=\widehat {ABD} =90^0

    =>∆ACH \sim ∆ADB (g - g)

    \begin{matrix} =>\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} \hfill \\ \Rightarrow AH.AD = AC.AB \hfill \\ \Rightarrow AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{12.15}}{6} = 30\left( {cm} ight) \hfill \\ \end{matrix}

    Vậy đường kính của đường tròn là 30cm.

  • Câu 19: Thông hiểu
    Tính diện tích phần hình theo yêu cầu

    Cho đường tròn (O;8cm) và dây AB căng cung có số đo 120^{0}. Diện tích phần hình giới hạn bởi hình quạt tròn AOB với dây AB bằng bao nhiêu? (với \pi = 3,14;\sqrt{3} = 1,73 và kết quả làm tròn đến chữ số hàng đơn vị).

    Hướng dẫn:

    Hình vẽ minh họa

    Diện tích hình quạt tròn AOB là:

    S_{AOB} = \frac{\pi nR^{2}}{360} = \frac{3,14.120.8^{2}}{360} = 67cm^{2}

    Diện tích tam giác OAB là:

    S_{AOB} = \frac{1}{2}OA.AB = \frac{1}{2}.\frac{R}{2}.R\sqrt{3}

    = \frac{R^{2}\sqrt{3}}{4} = \frac{8^{2}.1,73}{4} \approx 28\left( cm^{2} ight)

    Diện tích phần hình giới hạn bởi hình quạt tròn AOB và dây cung AB là:

    \Rightarrow S = 67 - 28 = 39\left( cm^{2} ight)

  • Câu 20: Thông hiểu
    Tính diện tích phần hình vẽ số 1

    Cho hình vẽ sau:

    Tính diện tích phần đánh số 1?

    Hướng dẫn:

    Diện tích hình vuông là (2.1,5)^{2} = 9cm^{2}

    Tổng diện tích các phần 2, 3, 4, 5 là:

    4.\frac{1}{4}\pi.1,5^{2} = 2,25\pi\left( cm^{2} ight)

    Khi đó diện tích phần 1 là: S_{1} = 9 - 2,25\pi \approx 1,93cm^{2}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (45%):
    2/3
  • Vận dụng (10%):
    2/3
  • Vận dụng cao (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 2 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 9 CD

Đăng nhập