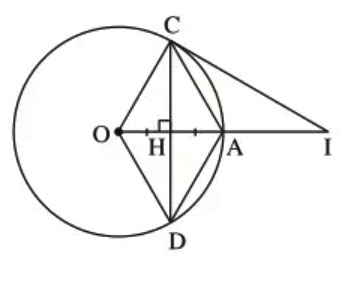
Cho đường tròn ![]() và một dây
và một dây ![]() không đi qua tâm. Vẽ đường thẳng
không đi qua tâm. Vẽ đường thẳng ![]() tiếp xúc với
tiếp xúc với ![]() tại
tại ![]() . Qua
. Qua ![]() vẽ đường thẳng vuông góc với
vẽ đường thẳng vuông góc với ![]() cắt đường thẳng
cắt đường thẳng ![]() tại
tại ![]() và cắt
và cắt ![]() tại
tại ![]() . Biết rằng
. Biết rằng ![]() . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng ![]() ?
?
Vì đường thẳng tiếp xúc với đường tròn
tại
nên
Mặt khác nên
Xét tam giác AOD vuông tại D và đường cao AD ta có:
Chứng minh được
Vậy