Lớp 10 Toán 10 - Kết nối tri thức

Hệ thức lượng trong tam giác

1. Định lý côsin trong tam giác 

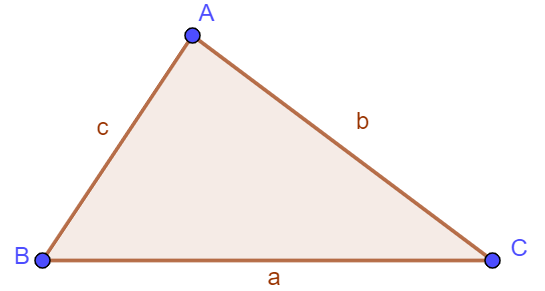
Cho tam giác ABC có AB=c,BC=a,CA=b, ta có:

  • a^2=b^2+c^2-2bc\cos A;
  • b^2=a^2+c^2-2ac\cos B;
  • c^2=a^2+b^2-2ab\cos C.

Hệ quả

  • \cos A=\frac{b^2+c^2-a^2}{2bc};
  • \cos B=\frac{a^2+c^2-b^2}{2ac};
  • \cos C=\frac{a^2+b^2-c^2}{2ab}.

Ví dụ 1: Cho tam giác ABC có \hat{A} =120^{\circ} và AB=3,AC=4. Tinh độ dài cạnh BC.

Hướng dẫn giải

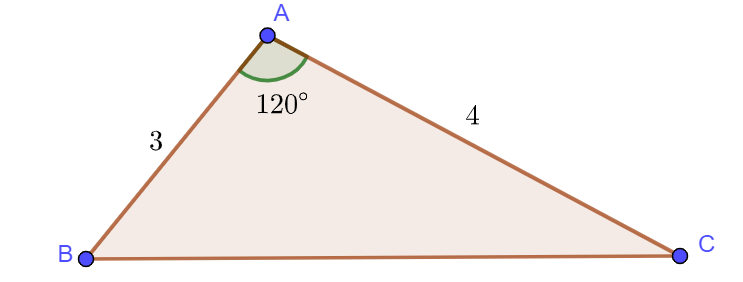
Áp dụng định lý côsin cho tam giác ABC, ta có:

BC^2=AB^2+AC^2-2AB.AC.\cos A=3^2+4^2-2.3.4.\cos 60^{\circ} =13.

Suy ra BC=\sqrt{13}.

Ví dụ 2: Cho tam giác ABC có a=19,b=6,c=15. Tính giá trị góc \hat A. (kết quả làm tròn đến hàng phần trăm)

Hướng dẫn giải

Áp dụng hệ quả của định lý côsin cho tam giác ABC, ta có:

\cos A= \frac{b^2+c^2-a^2}{2bc}=\frac{6^2+15^2-19^2}{2.6.15}=-\frac59.

Suy ra \hat A\approx 123,75^{\circ}.

2. Định lý sin trong tam giác

Cho tam giác ABC có AB=c,BC=a,CA=b và R là bán kính đường tròn ngoại tiếp tam giác ABC, ta có:

\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R

Ví dụ: Cho tam giác ABC có \hat A=120^{\circ} ,\hat C=45^{\circ} ,b=6. Tính số đo góc \hat B, độ dài a,c,R. (kết quả làm tròn đến hàng phần trăm)

Hướng dẫn giải

Ta có: \hat B=180^{\circ} -(\hat A+\hat C)=180^{\circ}-(120^{\circ} +45^{\circ} )=15^{\circ}.

Áp dụng định lý sin trong tam giác ABC: \frac{a}{\sin 120^{\circ} }=\frac 6{\sin 15^{\circ}}=\frac c{\sin45^{\circ}}=2R.

Suy ra: a=\sin 120^{\circ} .\frac 6{\sin 15^{\circ} } \approx 20,08, c=\sin 45^{\circ} .\frac 6{\sin 15^{\circ} } \approx 16,39,R=\frac 6{2\sin 15^{\circ} }\approx 11,59.

3. Các công thức tính diện tam giác

Cho tam giác ABC, ta kí hiệu:

  • AB=c,BC=a,CA=b;
  • h_a,h_b,h_c lần lượt là độ dài các đường cao kẻ từ A,B,C;
  • R là bán kính đường tròn ngoại tiếp;
  • r là bán kính đường tròn nội tiếp;
  • p= \frac{a+b+c}2 là nửa chu vi;
  • S là diện tích tam giác ABC.

Ta có các công thức tính diện tích tam giác sau:

  1. S_{ABC}=\frac12 a.h_a=\frac12 b.h_b =\frac12 c.h_c;
  2. S_{ABC}=\frac12bc\sin A=\frac12ac\sin B=\frac12ab\sin C;
  3. S_{ABC}=\frac {abc}{4R};
  4. S_{ABC}=p.r;
  5. S_{ABC}=\sqrt{p(p-a)(p-b))p-c)} (Công thức Heron).

Ví dụ 1: Cho tam giác ABC có a=5,b=6,c=7. Tính diện tích tam giác ABC.

Hướng dẫn giải

(Khi biết 3 cạnh của tam giác, ta sử dụng công thức Heron)

Ta có: p=\frac{a+b+c}2=\frac{5+6+7}2=9.

Áp dụng công thức Heron:

S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}=\sqrt{9(9-5)(9-6)(9-7)} = 6\sqrt6.

Ví dụ 2: Cho tam giác ABC có c=3,b=4,\hat A=120^{\circ}. Tính diện tích tam giác này.

Hướng dẫn giải

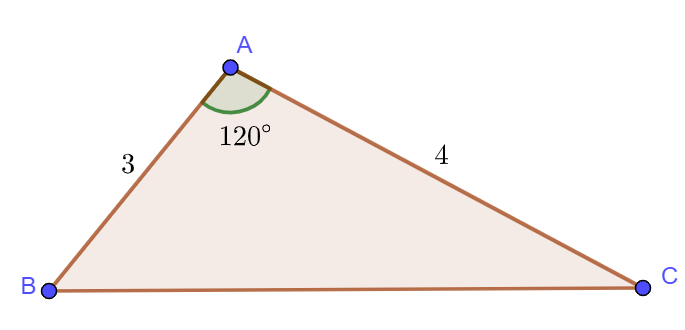
(Khi biết 2 cạnh và 1 góc xen giữa, ta sử dụng công thức số 2)

Ta có: S_{ABC}=\frac12bc\sin A=\frac12.3.4\sin 120^{\circ} =3\sqrt3.

4. Giải tam giác

Giải tam giác là đi tìm số đo tất cả các cạnh và tất cả các góc của tam giác.

Ví dụ: Giải tam giác ABC biết a=4,\hat B=60^{\circ} ,\hat C=45^{\circ}.

Hướng dẫn giải

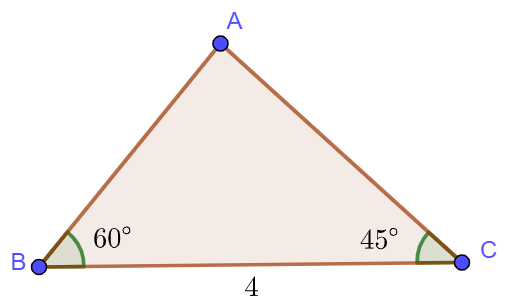
Ta có: \hat A=180^{\circ} -(\hat B+\hat C)=180^{\circ} -(60^{\circ} +45^{\circ} )=75^{\circ}.

Áp dụng định lý sin, ta có: \frac{4}{\sin 75^{\circ} }=\frac b{\sin 60^{\circ}}=\frac c{\sin45^{\circ}}=2R.

Suy ra: b=\sin 60^{\circ} .\frac 4{\sin 75^{\circ} } \approx 3,59, x=\sin 45^{\circ} .\frac 4{\sin 75^{\circ} } \approx =2,93, R=\frac 4{2\sin 75^{\circ} } \approx 2,07.

  • 16 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 KNTT