Tìm m để hàm số y = (2m−1)x + 7 đồng biến trên ℝ.
Hàm số y = (2m−1)x + 7 đồng biến trên ℝ khi 2m − 1 > 0 hay .
Tập xác định của hàm số 
là
Hàm số ⇒ Điều kiện: B(x) ≠ 0.
Hàm số Điều kiện: A(x) ≥ 0.
Ta có 9 − x2 ≥ 0 ⇔ (3−x)(3+x) ≥ 0 ⇔ − 3 ≤ x ≤ 3.
Hàm số xác định khi và chỉ khi
. Vậy x ∈ [ − 3; 3] ∖ {2}.
Tìm tập xác định D của hàm số
Hàm số xác định khi .
Vậy xác định của hàm số là D = ℝ ∖ {2}.
Xét sự biến thiên của hàm số trên khoảng (0;+∞). Khẳng định nào sau đây đúng?
Vậy hàm số nghịch biến trên khoảng (0;+∞).
Cho hàm số Khẳng định nào sau đây đúng?
TXĐ : nên ta loại đáp án C và D.
Xét
Với mọi và x1 < x2, ta có
Vậy hàm số đồng biến trên .
Hàm số f(x) có tập xác định ℝ và có đồ thị như hình vẽ
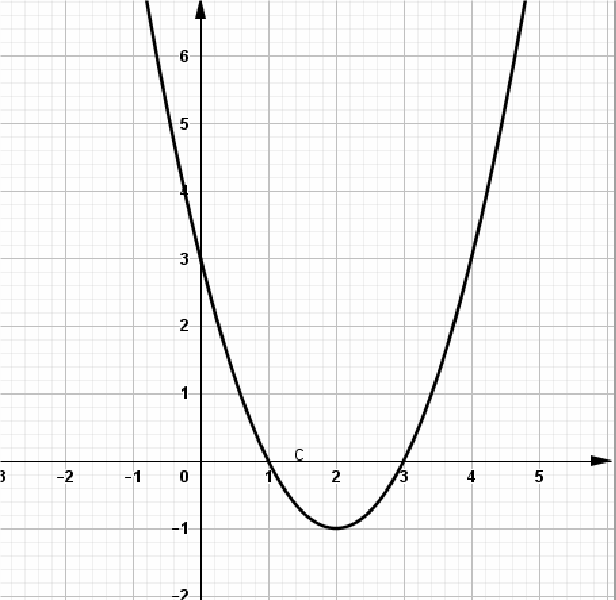
Mệnh đề nào sau đây đúng ?
Nhìn vào đồ thị hàm số ta có:
Đồ thị hàm số cắt trục hoành tại hai điểm M(1; 0), N(3; 0) ⇒ MN = 2 . Suy ra Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng 2là đúng.
Khẳng định nào về hàm số y = 3x + 5 là sai?
Hàm số y = 3x + 5 có hệ số a = 3 > 0 nên đồng biến trên ℝ, suy ra chọn đáp án Hàm số nghịch biến trên ℝ.
Tập xác định của hàm số là
Hàm số ⇒ Điều kiện: B(x) ≠ 0.
Hàm số Điều kiện: A(x) ≥ 0.
Hàm số có nghĩa khi
⇔ x ∈ [ − 1; 3) ∖ {2}.
Xét sự biến thiên của hàm số trên khoảng (1;+∞). Khẳng định nào sau đây đúng?
Ta có :
Với mọi x1, x2 ∈ (1;+∞) và x1 < x2. Ta có
Suy ra đồng biến trên (1;+∞).
Cho hàm số có đồ thị như hình vẽ
Khẳng định nào sau đây đúng:
Hàm số đồng biến trên khoảng (1;3).
Cho hai đường thẳng và . Mệnh đề nào sau đây đúng?
Cách 1: Gọi k1, k2 lần lượt là hệ số gốc của (d1)và (d2). Khi đó nên (d1)và (d2) không vuông góc nhau.
Xét hệ:
Vậy (d1)và (d2) cắt nhau.
Cách 2: Ta thấy nên (d1)và (d2) cắt nhau.
Xét tính đồng biến, nghịch biến của hàm số trên khoảng (−∞;−5) và trên khoảng (−5;+∞). Khẳng định nào sau đây đúng?
Ta có :
.
● Với mọi x1, x2 ∈ (−∞;−5) và x1 < x2. Ta có .
Suy ra đồng biến trên (−∞;−5).
● Với mọi x1, x2 ∈ (−5;+∞) và x1 < x2. Ta có .
Suy ra đồng biến trên (−5;+∞).
Tìm tập xác định của hàm số .
Điều kiện xác định: 4x2 − 4x + 1 ≥ 0 ⇔ (2x−1)2 ≥ 0 (luôn đúng với mọi x ∈ ℝ).
Do đó tập xác định D = ℝ.
Tìm tập xác định D của hàm số .
Hàm số xác định khi
⇔ x2 − 3x + 2 ≠ x2 − 7 ⇔ 9 ≠ 3x ⇔ x ≠ 3.
Vậy tập xác định của hàm số là D = ℝ ∖ {3}.
Xét sự biến thiên của hàm số trên khoảng (1;+∞). Khẳng định nào sau đây đúng?
Ta có :
Với mọi x1, x2 ∈ (1;+∞) và x1 < x2. Ta có
Suy ra đồng biến trên (1;+∞).
Tập xác định của hàm số là:
Điều kiện: 8 − 2x ≥ 0 ⇔ x ≤ 4. Vậy D = ( − ∞; 4].
Bằng phép tịnh tiến, từ đồ thị hàm số y = − 2x2suy ra đồ thị hàm số y = − 2x2 − 6x + 3 như thế nào?
Xét
Do đó tịnh tiến đồ thị hàm số y = − 2x2 để được đồ thị hàm số y = − 2x2 − 6x + 3 ta làm như sau:
Tịnh tiến liên tiếp đồ thị hàm số y = − 2x2 đi sang bên trái đơn vị và lên trên đi
đơn vị.
Tập xác định của hàm số là
Ta lấy hợp của tất cả các khoảng mà hàm số xác định.
Ta có :
• Khi x < 2: xác định khi
.
Suy ra D1 = (−∞;2).
• Khi x ≥ 2: xác định khi x + 7 ≥ 0 ⇔ x ≥ − 7.
Suy ra D1 = [2; + ∞).
Vậy TXĐ của hàm số là D = D1 ∪ D2 = (−∞;+∞) = ℝ.
Bằng phép tịnh tiến, đồ thị hàm số được suy ra từ đồ thị như thế nào?
Xét , ta có
.
Vậy đồ thị hàm số được suy ra từ đồ thị hàm số
bằng cách tịnh tiến sang phải 1 đơn vị.
Tập xác định của hàm số là:
Hàm số xác định ⇔ x − 1 ≥ 0 ⇔ x ≥ 1.
