Lớp 10 Toán 10 - Kết nối tri thức

Luyện tập Hàm số (Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Chọn khẳng định đúng

    Xét sự biến thiên của hàm số f(x) = x + \frac{1}{x} trên khoảng (1;+∞). Khẳng định nào sau đây đúng?

    Hướng dẫn:

    Ta có : f\left( x_{1} ight) - f\left( x_{2} ight) = \left( x_{1} + \frac{1}{x_{1}} ight) - \left( x_{2} + \frac{1}{x_{2}} ight) = \left( x_{1} - x_{2} ight) + \left( \frac{1}{x_{1}} - \frac{1}{x_{2}} ight) = \left( x_{1} - x_{2} ight)\left( 1 - \frac{1}{x_{1}x_{2}} ight).

    Với mọi x1, x2 ∈ (1;+∞) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} > 1 \\ x_{2} > 1 \\ \end{matrix} ight.\ \Rightarrow x_{1}.x_{1} > 1 \Rightarrow \frac{1}{x_{1}.x_{1}} < 1.

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = 1 - \frac{1}{x_{1}x_{2}} > 0\overset{}{ightarrow}f(x) đồng biến trên (1;+∞).

  • Câu 2: Thông hiểu
    Tìm tọa độ điểm

    Cho hàm số y = \frac{x + 1}{x - 1}. Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng − 2.

    Gợi ý:

    Thay giá trị tung độ  − 2 vào công thức hàm số để tìm ra hoành độ.

    Hướng dẫn:

    Gọi M0(x0;−2) là điểm thuộc đồ thị hàm số có tung độ bằng  − 2.

    Khi đó: \frac{x_{0} + 1}{x_{0} - 1} = - 2 \Leftrightarrow x_{0} + 1 = 2\left( 1 - x_{0} ight) \Leftrightarrow 3x_{0} = 1 \Leftrightarrow x_{0} = \frac{1}{3} \Rightarrow M\left( \frac{1}{3}; - 2 ight).

  • Câu 3: Vận dụng
    Chọn khẳng định đúng

    Xét sự biến thiên của hàm số f(x) = \frac{3}{x} trên khoảng (0;+∞). Khẳng định nào sau đây đúng?

    Hướng dẫn:

    Ta có f\left( x_{1} ight) - f\left( x_{2} ight) = \frac{3}{x_{1}} - \frac{3}{x_{2}} = \frac{3\left( x_{2} - x_{1} ight)}{x_{1}x_{2}} = - \frac{3\left( x_{1} - x_{2} ight)}{x_{1}x_{2}}.

    Với mọi x1, x2 ∈ (0;+∞) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} > 0 \\ x_{2} > 0 \\ \end{matrix} ight.\ \Rightarrow x_{1}.x > 0.

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = - \frac{3}{x_{1}x_{2}} < 0\overset{}{ightarrow}f(x) nghịch biến trên (0;+∞).

  • Câu 4: Nhận biết
    Chọn khẳng định đúng

    Chọn khẳng định đúng?

    Hướng dẫn:

    Lí thuyết định nghĩa hàm số đồng biến, nghịch biến: Hàm số y = f(x) được gọi là đồng biến trên K nếu ∀x1; x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).

  • Câu 5: Nhận biết
    Chọn khẳng định sai

    Cho hàm số y = f(x) xác định trên ℝ và đồ thị của nó được biểu diễn bởi hình bên. Khẳng định nào sau đây là sai?

    Hướng dẫn:

    Trên khoảng (2;+∞) đồ thị hàm số đi lên từ trái sang phải

    \overset{}{ightarrow} Hàm số đồng biến trên khoảng (2;+∞).

    Chọn đáp án Hàm số nghịch biến trên khoảng (2;+∞).

  • Câu 6: Nhận biết
    Tìm điểm thuộc đồ thị

    Điểm nào sau đây thuộc đồ thị của hàm số y = \frac{x - 2}{x(x - 1)}?

    Hướng dẫn:

    Thử trực tiếp thấy tọa độ của M(2;0) thỏa mãn phương trình hàm số.

  • Câu 7: Vận dụng
    Chọn khẳng định đúng

    Cho hàm số f(x) = \sqrt{2x - 7}. Khẳng định nào sau đây đúng?

    Hướng dẫn:

    TXĐ : D = \left\lbrack \frac{7}{2}; + \infty ight) nên ta loại đáp án C và D.

    Xét f\left( x_{1} ight) - f\left( x_{2} ight) = \sqrt{2x_{1} - 7} - \sqrt{2x_{2} - 7} = \frac{2\left( x_{1} - x_{2} ight)}{\sqrt{2x_{1} - 7} + \sqrt{2x_{2} - 7}}.

    Với mọi x_{1},\ x_{2} \in \left( \frac{7}{2}; + \infty ight) và x1 < x2, ta có \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = \frac{2}{\sqrt{2x_{1} - 7} + \sqrt{2x_{2} - 7}} > 0.

    Vậy hàm số đồng biến trên \left( \frac{7}{2}; + \infty ight).

  • Câu 8: Thông hiểu
    Tìm hoành độ của điểm

    Cho hàm số y = \left\{ \begin{matrix} - 2x + 1 & khi & x \leq - 3 \\ \frac{x + 7}{2} & khi & x > - 3 \\ \end{matrix} ight.. Biết f(x0) = 5 thì x0 là

    Gợi ý:

    Thay giá trị tung độ 5 vào công thức hàm số để tìm ra hoành độ.

    Hướng dẫn:

    TH1. x0 ≤  − 3: Với f(x0) = 5 ⇔  − 2x0 + 1 = 5 ⇔ x0 =  − 2 (Loại).

    TH2. x0 >  − 3: Với f\left( x_{0} ight) = 5 \Leftrightarrow \frac{x_{0} + 7}{2} = 5 \Leftrightarrow x_{0} = 3 (thỏa mãn).

  • Câu 9: Nhận biết
    Tìm hàm số đồng biến

    Hàm số nào sau đây đồng biến trên tập xác định của nó?

    Hướng dẫn:

    y = 3x + 1 có a = 3 > 0 nên hàm số đồng biến trên TXĐ.

  • Câu 10: Vận dụng
    Tìm hàm số thỏa mãn đồ thị

    Đường gấp khúc trong hình vẽ là dạng đồ thị của một trong bốn hàm số được liệt kê trong các phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

    Hướng dẫn:

    Đồ thị hàm số đi qua các điểm (0;1) và (1;0) nên chỉ có hàm số y = 1 − |x| thỏa mãn.

    Chọn y = 1 − |x|.

  • Câu 11: Thông hiểu
    Tính giá trị hàm số tại điểm

    Cho hàm số f(x) = \left\{ \begin{matrix} \frac{2x + 3}{x + 1} & khi & x \geq 0 \\ \frac{\sqrt[3]{2 + 3x}}{x - 2} & khi & - 2 \leq x < 0 \\ \end{matrix} ight.. Ta có kết quả nào sau đây đúng?

    Hướng dẫn:

    f( - 1) = \frac{\sqrt[3]{2 - 3}}{- 1 - 2} = \frac{1}{3}; f(2) = \frac{2.2 + 3}{2 + 1} = \frac{7}{3}.

  • Câu 12: Nhận biết
    Tìm hàm số nghịch biến

    Trong các hàm số sau, hàm số nào nghịch biến trên ℝ?

    Hướng dẫn:

    Hàm số y = ax + b với a ≠ 0 nghịch biến trên ℝ khi và chỉ khi a < 0.

  • Câu 13: Vận dụng
    Chọn khẳng định đúng

    Xét tính đồng biến, nghịch biến của hàm số f(x) = \frac{x - 3}{x + 5} trên khoảng (−∞;−5) và trên khoảng (−5;+∞). Khẳng định nào sau đây đúng?

    Hướng dẫn:

    Ta có : f\left( x_{1} ight) - f\left( x_{2} ight) = \left( \frac{x_{1} - 3}{x_{1} + 5} ight) - \left( \frac{x_{2} - 3}{x_{2} + 5} ight) = \frac{\left( x_{1} - 3 ight)\left( x_{2} + 5 ight) - \left( x_{2} - 3 ight)\left( x_{1} + 5 ight)}{\left( x_{1} + 5 ight)\left( x_{2} + 5 ight)} = \frac{8\left( x_{1} - x_{2} ight)}{\left( x_{1} + 5 ight)\left( x_{2} + 5 ight)}.

    ● Với mọi x1, x2 ∈ (−∞;−5) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} < - 5 \\ x_{2} < - 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x_{1} + 5 < 0 \\ x_{2} + 5 < 0 \\ \end{matrix} ight..

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = \frac{8}{\left( x_{1} + 5 ight)\left( x_{2} + 5 ight)} > 0\overset{}{ightarrow}f(x) đồng biến trên (−∞;−5).

    ● Với mọi x1, x2 ∈ (−5;+∞) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} > - 5 \\ x_{2} > - 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x_{1} + 5 > 0 \\ x_{2} + 5 > 0 \\ \end{matrix} ight..

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = \frac{8}{\left( x_{1} + 5 ight)\left( x_{2} + 5 ight)} > 0\overset{}{ightarrow}f(x) đồng biến trên (−5;+∞).

    Chọn Hàm số đồng biến trên các khoảng (−∞;−5) và (−5;+∞).

  • Câu 14: Nhận biết
    Tìm tập xác định

    Tìm tập xác định của hàm số y = \sqrt{2x^{2} - 5x + 2}.

    Hướng dẫn:

    Hàm số xác định \Leftrightarrow 2x^{2} - 5x + 2 \geq 0 \Leftrightarrow \left\lbrack \begin{matrix} x \leq \frac{1}{2} \\ x \geq 2 \\ \end{matrix} ight..

    Vậy tập xác định: D = \left( - \infty;\ \frac{1}{2} ightbrack \cup \lbrack 2;\ + \infty).

  • Câu 15: Vận dụng
    Tìm m để hàm số xác định

    Tìm m để hàm số y = \frac{\sqrt{x - 2m + 3}}{x - m} + \frac{3x - 1}{\sqrt{- x + m + 5}} xác định trên khoảng (0;1).

    Gợi ý:

    Hàm số y = \frac{A(x)}{B(x)} ⇒ Điều kiện: B(x) ≠ 0.

    Hàm số y = \sqrt[{2k}]{A(x)}\ \left( k\mathbb{\in N}* ight) \Rightarrow Điều kiện: A(x) ≥ 0.

    Hàm số y = \frac{A(x)}{\sqrt[{2k}]{B(x)}}\ \left( k\mathbb{\in N}* ight) \Rightarrow Điều kiện: B(x) ≥ 0.

    Hướng dẫn:

    *Gọi D là tập xác định của hàm số y = \frac{\sqrt{x - 2m + 3}}{x - m} + \frac{3x - 1}{\sqrt{- x + m + 5}}.

    *x \in D \Leftrightarrow \left\{ \begin{matrix} x - 2m + 3 \geq 0 \\ x - m\boxed{=}0 \\ - x + m + 5 > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 2m - 3 \\ x\boxed{=}m \\ x < m + 5 \\ \end{matrix} ight..

    *Hàm số y = \frac{\sqrt{x - 2m + 3}}{x - m} + \frac{3x - 1}{\sqrt{- x + m + 5}} xác định trên khoảng (0;1)

    \Leftrightarrow (0;1) \subset D \Leftrightarrow \left\{ \begin{matrix} 2m - 3 \leq 0 \\ m + 5 \geq 1 \\ m otin (0;1) \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m \leq \frac{3}{2} \\ m \geq - 4 \\ \left\lbrack \begin{matrix} m \geq 1 \\ m \leq 0 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow m \in \lbrack - 4;0brack \cup \left\lbrack 1;\frac{3}{2} ightbrack.

  • Câu 16: Thông hiểu
    Tính giá trị hàm số tại điểm

    Cho hàm số f(x) = \left\{ \begin{matrix} \frac{2\sqrt{x - 2} - 3}{x - 1} & khi & x \geq 2 \\ x^{2} + 2 & khi & x < 2 \\ \end{matrix} ight.. Tính P = f(2) + f(−2).

    Gợi ý:

    Tính giá trị hàm số tại điểm có hoành độ 2 và  − 2 rồi cộng lại.

    Hướng dẫn:

    Ta có: f(2) + f( - 2) = \frac{2\sqrt{2 - 2} - 3}{2 - 1} + ( - 2)^{2} + 2 \Rightarrow P = 3.

  • Câu 17: Vận dụng
    Chọn khẳng định đúng

    Xét tính đồng biến, nghịch biến của hàm số f(x) = x2 − 4x + 5 trên khoảng (−∞;2) và trên khoảng (2;+∞). Khẳng định nào sau đây đúng?

    Hướng dẫn:

    Ta có : f(x1) − f(x2) = (x12−4x1+5) − (x22−4x2+5) = (x12−x22) − 4(x1−x2) = (x1−x2)(x1+x2−4).

    ● Với mọi x1, x2 ∈ (−∞;2) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} < 2 \\ x_{2} < 2 \\ \end{matrix} ight.\ \Rightarrow x_{1} + x_{2} < 4.

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = \frac{\left( x_{1} - x_{2} ight)\left( x_{1} + x_{2} - 4 ight)}{x_{1} - x_{2}} = x_{1} + x_{2} - 4 < 0.

    Vậy hàm số nghịch biến trên (−∞;2).

    ● Với mọi x1, x2 ∈ (2;+∞) và x1 < x2. Ta có \left\{ \begin{matrix} x_{1} > 2 \\ x_{2} > 2 \\ \end{matrix} ight.\ \Rightarrow x_{1} + x_{2} > 4.

    Suy ra \frac{f\left( x_{1} ight) - f\left( x_{2} ight)}{x_{1} - x_{2}} = \frac{\left( x_{1} - x_{2} ight)\left( x_{1} + x_{2} - 4 ight)}{x_{1} - x_{2}} = x_{1} + x_{2} - 4 > 0.

    Vậy hàm số đồng biến trên (2;+∞).

  • Câu 18: Vận dụng
    Chọn khẳng định đúng

    Hàm số f(x) có tập xác định ℝ và có đồ thị như hình vẽ

     

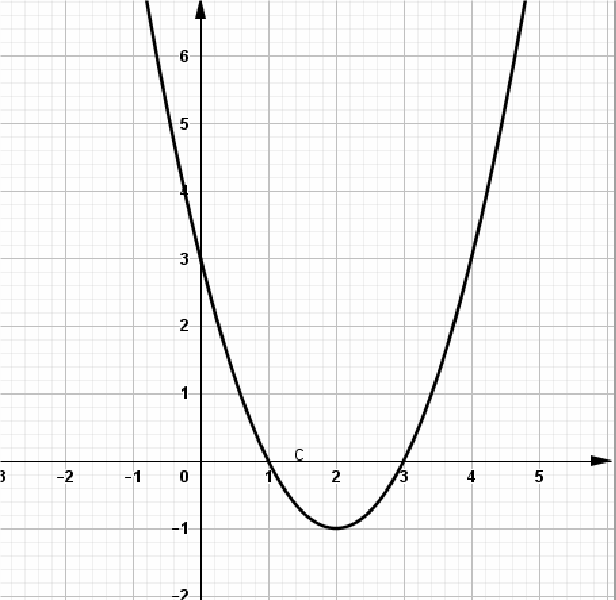
    Mệnh đề nào sau đây đúng ?

    Hướng dẫn:

    Nhìn vào đồ thị hàm số ta có:

    Đồ thị hàm số cắt trục hoành tại hai điểm M(1; 0), N(3; 0) ⇒ MN = 2 . Suy ra Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng 2là đúng.

  • Câu 19: Nhận biết
    Chọn khẳng định sai

    Cho hàm số y = f(x) có tập xác định là [ − 1; 3] và đồ thị của nó được biểu diễn bởi hình bên.

    Khẳng định nào sau đây là sai?

    Hướng dẫn:

    Trên khoảng (0;2) đồ thị hàm số đi ngang từ trái sang phải

    \overset{}{ightarrow} Hàm số không đổi trên khoảng (0;2).

    Trên khoảng (2;3) đồ thị hàm số đi lên từ trái sang phải

    \overset{}{ightarrow} Hàm số đồng biến trên khoảng (2;3).

    Chọn đáp án Hàm số đồng biến trên khoảng (2;3).

  • Câu 20: Nhận biết
    Tìm tập xác định

    Tập xác định của hàm số y = \frac{2 - x}{x^{2} - 4x} là:

    Hướng dẫn:

    Hàm số xác định \Leftrightarrow x^{2} - 4x eq 0 \Leftrightarrow \left\{ \begin{matrix} x eq 0 \\ x eq 4 \\ \end{matrix} ight.. Vậy D = ℝ ∖ {0;4}.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (20%):
    2/3
  • Vận dụng (40%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 46 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 KNTT

Đăng nhập