Lớp 8 Toán 8 - Chân trời sáng tạo

Luyện tập Các trường hợp đồng dạng của hai tam giác vuông

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Chọn đáp án đúng

    Cho hình chữ nhật ABCD có E là trung điểm của AB. Tia DE cắt AC ở F, cắt CB ở G. Chọn câu đúng.

    Hướng dẫn:

    Hình vẽ minh họa

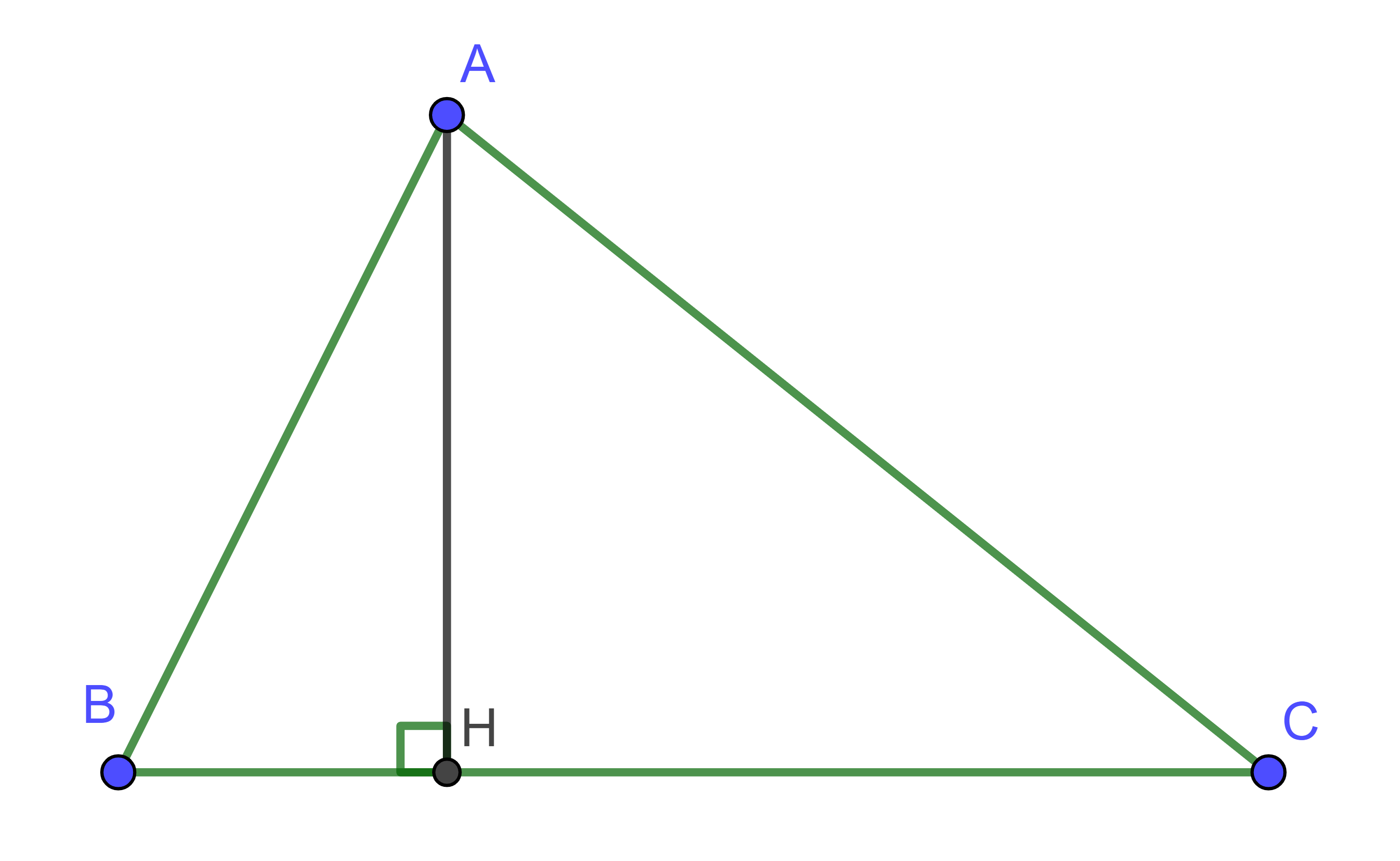
    Các trường hợp đồng dạng của tam giác

    Ta có AB // CD (vì ABCD là hình chữ nhật)

    Theo định lí Thales ta có: \frac{{EF}}{{FD}} = \frac{{EA}}{{DC}}

    Vì E là trung điểm của AB nên 

    \begin{array}{l}EA = EB = \dfrac{1}{2}AB = \dfrac{1}{2}CD\\ \Rightarrow \dfrac{{EF}}{{FD}} = \dfrac{{AE}}{{CD}} = \dfrac{1}{2}\left( * ight)\\ \Rightarrow FD = 2EF\end{array}

    Xét hai tam giác vuông ΔAED và ΔBEG ta có:

    % MathType!MTEF!2!1!+-% feaahCart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9\begin{array}{l}\widehat {DAE} = \widehat {GBE} = {90^0}\\\widehat {AED} = \widehat {BEG}\left( {dd} ight)\\AE = EB\left( {gt} ight)\\ \Rightarrow \Delta AED = \Delta BEG\left( {g - c - g} ight)\\ \Rightarrow ED = EG\end{array}

    Ta có: 

    \begin{array}{l}\dfrac{{FD}}{{FG}} = \dfrac{{2EF}}{{FE + EG}} = \dfrac{{2EF}}{{FE + EF + FD}}\\ = \dfrac{{2EF}}{{FE + EF + 2EF}} = \dfrac{{2EF}}{{4EF}} = \dfrac{1}{2}\left( {**} ight)\end{array}

    Từ (*) và (**) suy ra \frac{{EF}}{{FD}} = \frac{{FD}}{{FG}} \Rightarrow D{F^2} = EF.FG

  • Câu 2: Vận dụng
    Điền đáp án vào ô trống

    Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?

    {S_{ABC}} =39 cm^2

    Đáp án là:

    Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?

    {S_{ABC}} =39 cm^2

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Xét hai tam giác vuông AHB và tam giác CAB ta có:

    Góc B chung

    \begin{array}{l} \Rightarrow \Delta AHB \sim \Delta CAB\left( {g - g} ight)\\ \Rightarrow \dfrac{{AB}}{{CB}} = \dfrac{{HB}}{{AB}}\\ \Rightarrow A{B^2} = HB.BC = 4.13 = 52 \end{array}

    Xét hai tam giác vuông AHC và tam giác BAC ta có:

    Góc B chung

    \begin{array}{l} \Rightarrow \Delta AHC \sim \Delta BAC\left( {g - g} ight)\\ \Rightarrow \dfrac{{AC}}{{BC}} = \dfrac{{HC}}{{AC}}\\ \Rightarrow A{C^2} = HC.BC = 9.13 = 117 \end{array}

    % MathType!MTEF!2!1!+- \begin{array}{l} \Rightarrow \left\{ \begin{array}{l} AB = \sqrt {52} \\ AC = \sqrt {117} \end{array} ight.\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = 39\left( {c{m^2}} ight) \end{array}

  • Câu 3: Nhận biết
    Chọn đáp án đúng

    Cho hai tam giác vuông. Điều kiện để hai tam giác vuông đó đồng dạng là:

    Hướng dẫn:

    Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn kết luận đúng.

    Hướng dẫn:

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Áp dụng định lí Pythagore cho tam giác vuông ABC ta tính được BC = 10cm

    Có BD là phân giác của góc B

    Áp dụng tính chất đường phân giác trong tam giác suy ra

    \frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\left( * ight)

    Mặt khác 

    \begin{matrix} \Rightarrow \dfrac{{AD}}{{DC + AD}} = \dfrac{{AB}}{{BC + AB}} \hfill \\ \Rightarrow \dfrac{{AD}}{{DC + AD}} = \dfrac{6}{{6 + 10}} \hfill \\ \Rightarrow \dfrac{{AD}}{{DC + AD}} = \dfrac{3}{8}\left( {**} ight) \hfill \\ \end{matrix}

    Từ (*) và (**) suy ra \left\{ {\begin{array}{*{20}{c}} {AD = 3cm} \\ {DC = 5cm} \end{array}} ight.

  • Câu 5: Thông hiểu
    Tính độ dài các đoạn thẳng

    Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.

    Tính độ dài các đoạn AD, DC lần lượt là

    Hướng dẫn:

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Áp dụng định lí Pythagore cho tam giác vuông ABC ta tính được BC = 10cm

    Có BD là phân giác của góc B

    Áp dụng tính chất đường phân giác trong tam giác suy ra

    \frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\left( * ight)

    Mặt khác:

    \begin{matrix} \dfrac{{AD}}{{DC + AD}} = \dfrac{{AB}}{{BC + AB}} \hfill \\ \Rightarrow \dfrac{{AD}}{{DC + AD}} = \dfrac{6}{{6 + 10}} \hfill \\ \Rightarrow \dfrac{{AD}}{{DC + AD}} = \dfrac{3}{8}\left( {**} ight) \hfill \\ \end{matrix}

    Từ (*) và (**) suy ra \left\{ {\begin{array}{*{20}{c}} {AD = 3cm} \\ {DC = 5cm} \end{array}} ight.

  • Câu 6: Thông hiểu
    Chọn khẳng định đúng

    Đáp án nào không thích hợp để điền vào chỗ trống trong phát biểu dưới đây?

    "Nếu hai tam giác đồng dạng với nhau thì: ..."

    Hướng dẫn:

    Nếu hai tam giác đồng dạng với nhau thì:

    - Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

    - Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

    - Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

    - Tỉ số các chu vi bằng tỉ số đồng dạng.

    Vậy đáp án không thích hợp điền vào chỗ trống là: "Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng."

  • Câu 7: Nhận biết
    Chọn đáp án đúng

    Cho Δ ABC và Δ MNP có \widehat A = \widehat M = {90^0};\frac{{AB}}{{MN}} = \frac{{CB}}{{NP}}. Chọn kết luận đúng?

    Hướng dẫn:

    Ta có:

    \left\{ \begin{array}{l}\widehat A = \widehat M = {90^0}\\\dfrac{{AB}}{{MN}} = \dfrac{{CB}}{{NP}}\end{array} ight. \Rightarrow \Delta ABC \sim \Delta MPN\left( {c - g - c} ight)

  • Câu 8: Thông hiểu
    Xét tính đúng sai của các đáp án

    Cho tam giác MNP vuông ở M và có đường cao MK.

    a) ΔKNM ~\simΔMNP \sim ΔKMP Đúng || Sai

    b) MK^2 = NK.PKĐúng || Sai

    Đáp án là:

    Cho tam giác MNP vuông ở M và có đường cao MK.

    a) ΔKNM ~\simΔMNP \sim ΔKMP Đúng || Sai

    b) MK^2 = NK.PKĐúng || Sai

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Xét hai tam giác vuông KNM và tam giác MNP có:

    Góc N chung

    \Rightarrow \Delta KNM \sim \Delta MNP\left( {g - g} ight)\left( 1 ight)

    Xét hai tam giác vuông KMP và tam giác MNP có:

    Góc P chung

    \Rightarrow \Delta KMP \sim \Delta MNP\left( {g - g} ight)\left( 2 ight)

    Từ (1) và (2) \Rightarrow \Delta KNM \sim \Delta KMP 

    Vậy ΔKNM ~\simΔMNP \sim ΔKMP đúng

    Theo chứng minh trên ta có:

    \begin{array}{l}\Delta KNM \sim \Delta KMP\\ \Rightarrow \dfrac{{MK}}{{PK}} = \dfrac{{NK}}{{MK}}\\ \Rightarrow M{K^2} = NK.PK\end{array}

    Vậy MK^2 = NK.PK đúng

  • Câu 9: Nhận biết
    Xác định tính đúng sai của các mệnh đề

    Cho các mệnh đề sau:

    (I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

    (II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

    Hãy xác định tính đúng sai của mệnh đề.

    Hướng dẫn:

    Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

    Vậy (I) đúng, (II) sai

  • Câu 10: Vận dụng
    Tính độ dài CE

    Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

    Hướng dẫn:

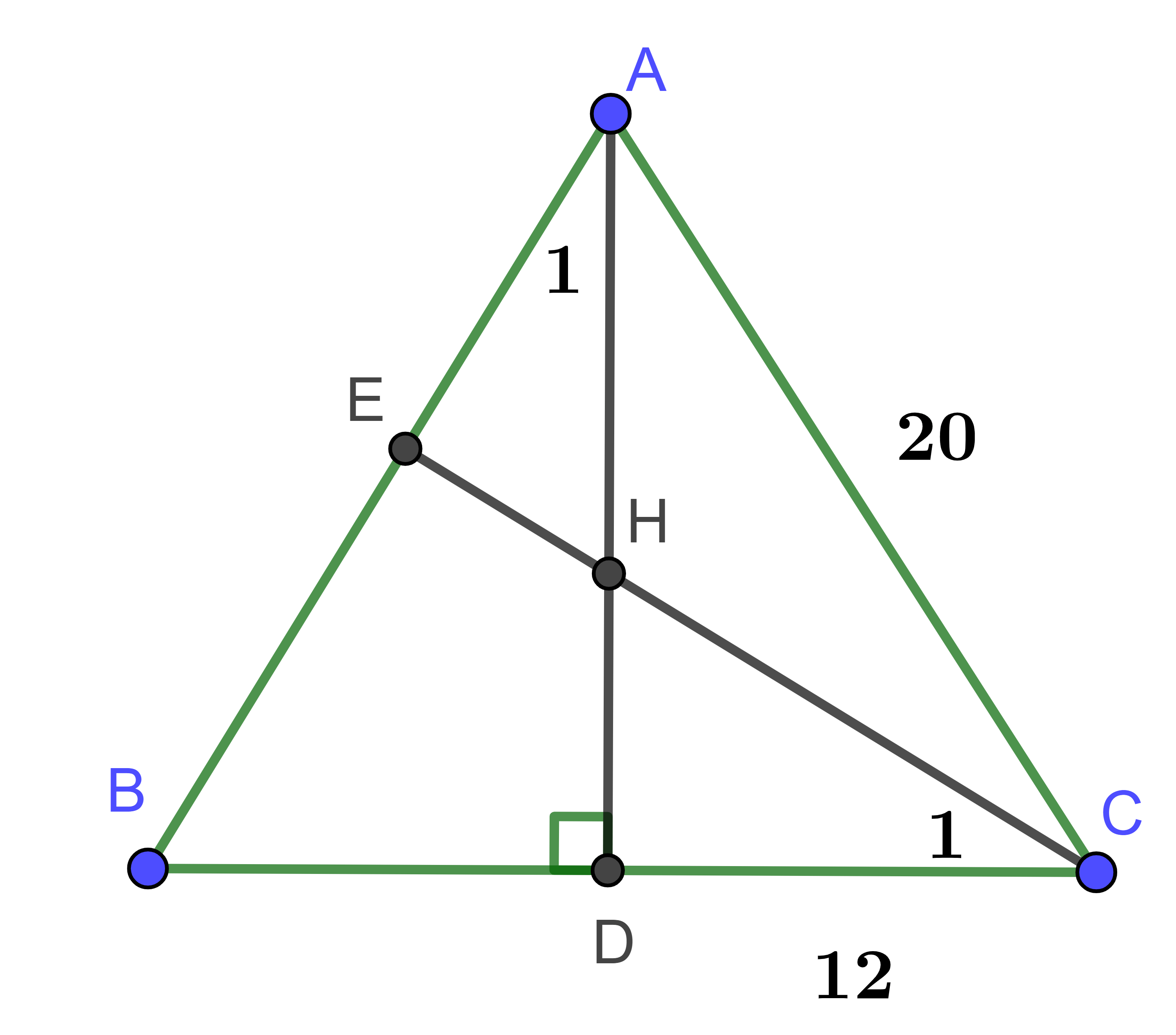
    Hình vẽ minh họa

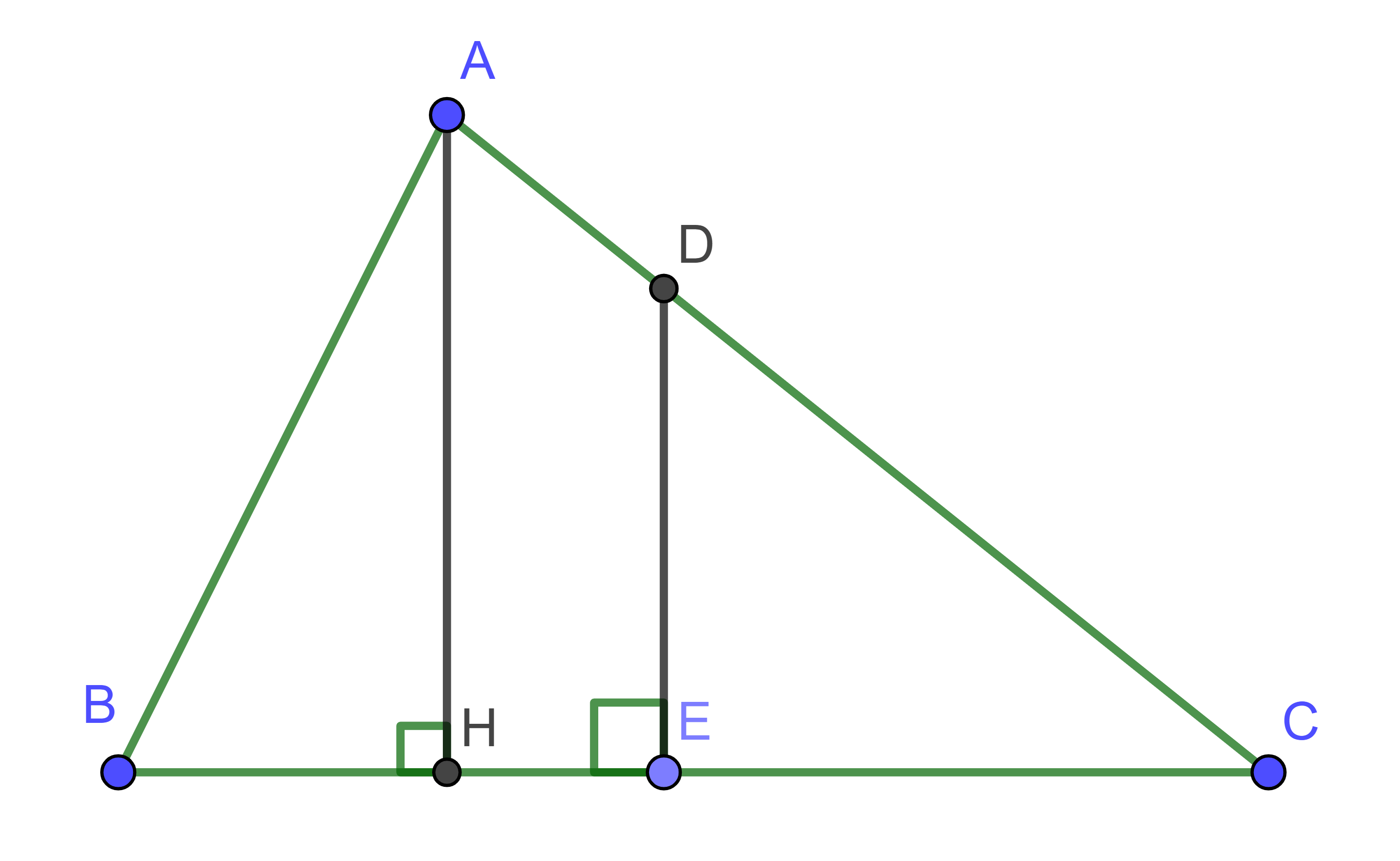
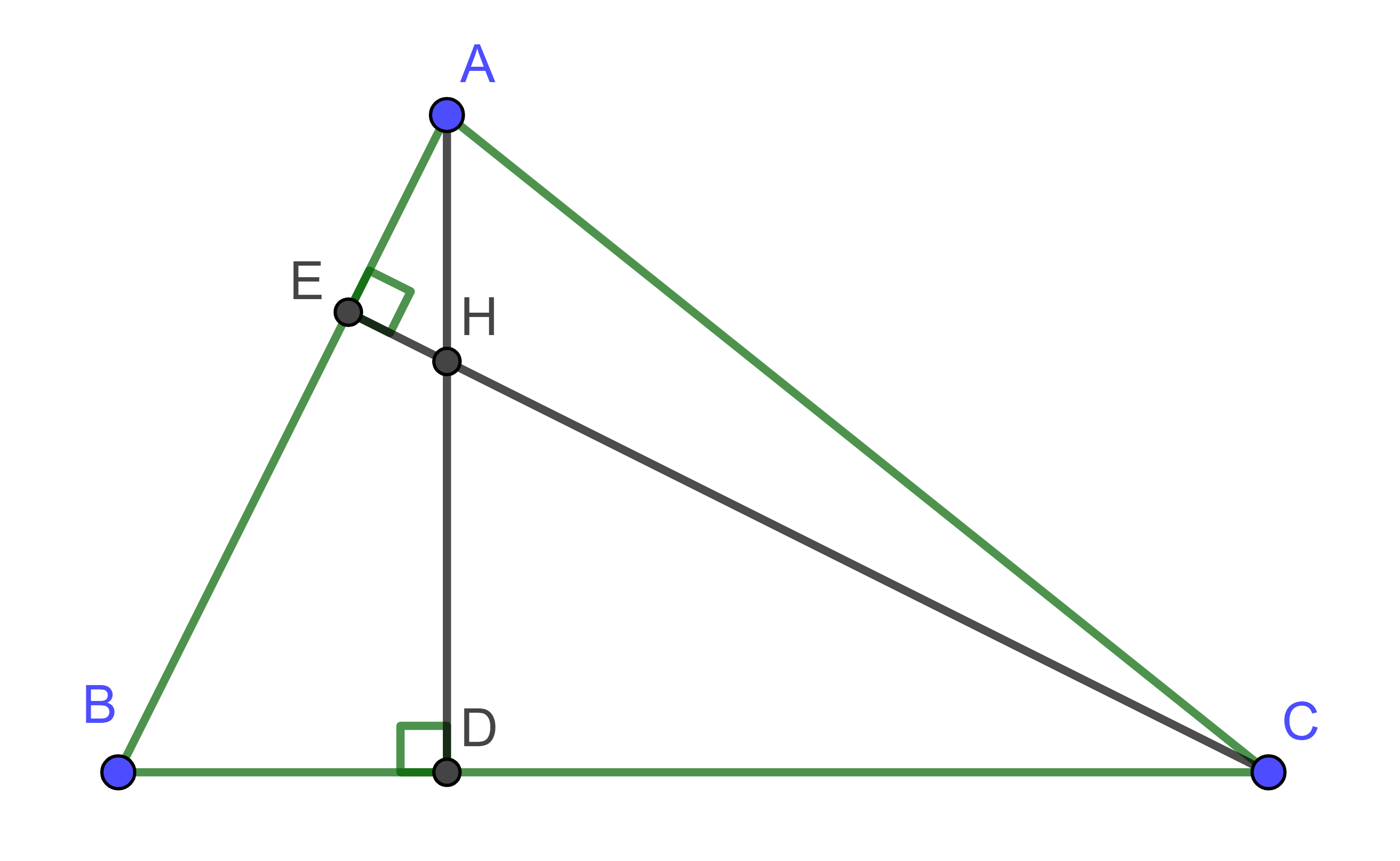
    Các trường hợp đồng dạng của tam giác vuông

    Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

    Xét ΔAHC và ΔABC có

    Góc C chung 

    \begin{array}{l}\widehat {AHC} = \widehat {BAC} = {90^0}\\ \Rightarrow \Delta AHC\; \sim \Delta BAC(g - g)\end{array}

    Ta có: \left\{ \begin{array}{l}{S_{DEC}} = \dfrac{1}{2}{S_{ABC}}\\\dfrac{{{S_{AHC}}}}{{{S_{ABC}}}} = \dfrac{{18}}{{25}}\end{array} ight. \Rightarrow \dfrac{{{S_{DEC}}}}{{{S_{AHC}}}} = \dfrac{{25}}{{36}} = {\left( {\frac{5}{6}} ight)^2}\left( * ight)

    Vì DE // AH (cùng vuông góc với BC) nên 

    \begin{array}{l} \Rightarrow \Delta DEC\; \sim \Delta AHC(g - g)\\ \Rightarrow \dfrac{{{S_{DEC}}}}{{{S_{AHC}}}} = {\left( {\dfrac{{EC}}{{HC}}} ight)^2}\left( {**} ight)\end{array}

    Từ (*) và (**) suy ra \frac{{EC}}{{HC}} = \frac{5}{6} \Rightarrow EC = 15\left( {cm} ight)

  • Câu 11: Thông hiểu
    Chọn đáp án sai

    Tam giác ABC vuông tại A có đường cao AH. Cho biết AB = 3cm; AC = 4cm. Chọn kết luận không đúng.

    Hướng dẫn:

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác

    Áp dụng định lý Pythagore vào tam giác vuông ABC ta có:

    A{B^2} + A{C^2} = B{C^2} \Rightarrow BC = 5cm

    Xét hai tam giác vuông ABC và HBA có:

    Góc B chung

    \widehat {BAC} = \widehat {AHB} = {90^0}

    => ΔABC \sim ΔHBA (g - g)

    \begin{array}{l} \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} = \dfrac{{AC}}{{HA}}\\ \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{9}{5} = 1,8\left( {cm} ight)\\ \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\left( {cm} ight)\end{array}

    =>HA = 2,4cm; HB = 1,8cm; HC = 3,2cm; BC = 5cm

    Vậy kết luận sai là BC = 6cm

  • Câu 12: Vận dụng
    Tính chiều cao của cây

    Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36m. Sau khi người ấy lùi ra xa cách cọc 0,64m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng, Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65m.

    Hướng dẫn:

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Xét ΔBFE và ΔBNM ta có:

    B chung

    \widehat {BEF} = \widehat {BMN} (vì EF // MN, cặp góc đồng vị bằng nhau)

    => ΔBFE ~ ΔBNM (g - g)

    \begin{array}{l} \Rightarrow \dfrac{{BF}}{{BN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + FN}} = \dfrac{{FE}}{{NM}}\\ \Leftrightarrow \dfrac{{BF}}{{BF + 0,64}} = \dfrac{{1,65}}{{2,45}}{m{ }}\\\begin{array}{*{20}{l}}{ \Leftrightarrow {m{ }}1,65\left( {BF + 0,64} ight) = 2,45.BF}\\{ \Leftrightarrow {m{ }}BF = 1,32m}\end{array}\end{array}

    Xét ΔBFE và ΔBCA có:

    B chung

    \widehat {BEF} = \widehat {BAC} (vì EF // AC, cặp góc đồng vị bằng nhau)

    \begin{array}{*{20}{l}}{ = > \Delta BFE\sim\Delta BCA\left( {g - g} ight)}\\\begin{array}{l} \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{BF}}{{BF + FN + NC}} = \dfrac{{FE}}{{CA}}{m{ }}\\ \Leftrightarrow \dfrac{{1,32}}{{1,32 + 0,64 + 1,36}} = \dfrac{{1,65}}{{CA}}\end{array}\\{ = > CA = 4,15m}\end{array}

    Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15m.

  • Câu 13: Thông hiểu
    Tính độ dài cạnh AB

    Cho tam giác ABC cân tại A. Đường thẳng qua C và vuông góc AB tại E. Tính AB, biết BC = 24cm, BD = 12cm và BE = 9cm.

    Hướng dẫn:

     Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Kẻ đường cao AD

    Xét tam giác CBE và tam giác ABD có:

    Góc B chung

    \begin{array}{l}\widehat {BEC} = \widehat {ADB} = {90^0}\\ \Rightarrow \Delta CBE \sim \Delta ABD\left( {g - g} ight)\\ \Rightarrow \dfrac{{BC}}{{AB}} = \dfrac{{BE}}{{BD}} \Rightarrow \dfrac{{24}}{{AB}} = \dfrac{9}{{12}} \Rightarrow AB = 32\left( {cm} ight)\end{array}

  • Câu 14: Thông hiểu
    Tính độ dài AH

    Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là:

    Hướng dẫn:

    Hình vẽ minh họa

    Các trường hợp đồng dạng của tam giác vuông

    Xét tam giác ABC cân tại A ta có:

    BD = DC = \frac{{BC}}{2} = \frac{{24}}{2} = 12\left( {cm} ight)

    Áp dụng định lí Pythagore cho tam giác ACD vuông tại D ta có:

    \begin{array}{l}A{D^2} = A{C^2} - D{C^2} = {20^2} - {12^2} = {16^2}\\ \Rightarrow AD = 16\left( {cm} ight)\end{array}

    Xét tam giác CDH và tam giác ADB ta có:

    \begin{array}{l}\widehat {CDH} = \widehat {ADB} = {90^0}\\\widehat {{C_1}} = \widehat {{A_1}}\\ \Rightarrow \Delta CDH \sim \Delta ADB\left( {g - g} ight)\\ \Rightarrow \dfrac{{HD}}{{BD}} = \dfrac{{HC}}{{AB}} = \dfrac{{CD}}{{AD}} \Rightarrow \dfrac{{HD}}{{12}} = \dfrac{{HC}}{{20}} = \dfrac{3}{4}\\ \Rightarrow HD = \dfrac{{12.3}}{4} = 9 \Rightarrow AH = AD - HD = 7\left( {cm} ight)\end{array}

  • Câu 15: Nhận biết
    Chọn kết luận đúng nhất

    Cho hai tam giác ABC và DEF có \widehat A = \widehat D = {90^0}, AB = 3cm, BC = 5cm,EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?

    Hướng dẫn:

     Ta có:

    \begin{array}{l}\left\{ \begin{array}{l}\widehat A = \widehat D = {90^0}\\\dfrac{{AB}}{{DF}} = \dfrac{{CB}}{{EF}} = \dfrac{1}{2}\end{array} ight.\\ \Rightarrow \Delta ABC \sim \Delta DFE\left( {c - g - c} ight)\end{array}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (27%):
    2/3
  • Thông hiểu (47%):
    2/3
  • Vận dụng (27%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 24 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 8 CTST

Đăng nhập