Tìm hai đường thẳng song song trong hình vẽ dưới đây
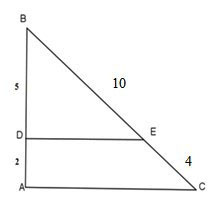
Ta có:
Theo định lý đảo của định lý Talet, ta suy ra .
Tìm hai đường thẳng song song trong hình vẽ dưới đây

Ta có:
Theo định lý đảo của định lý Talet, ta suy ra .
Cho hình vẽ:
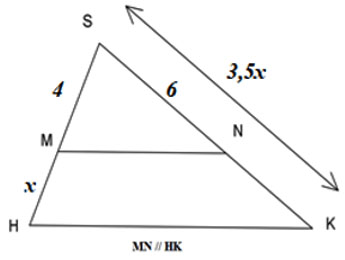
Tìm giá trị của 2x.
Ta có: , áp dụng định lí Thales ta có:
Cho tam giác ABC có AB = 8cm, điểm D thuộc cạnh AB sao cho AD = 4cm. Kẻ DE song song với BC (E ∈ AC), kẻ EF song song với CD (F ∈ AB). Tính độ dài AF.
Hình vẽ minh họa
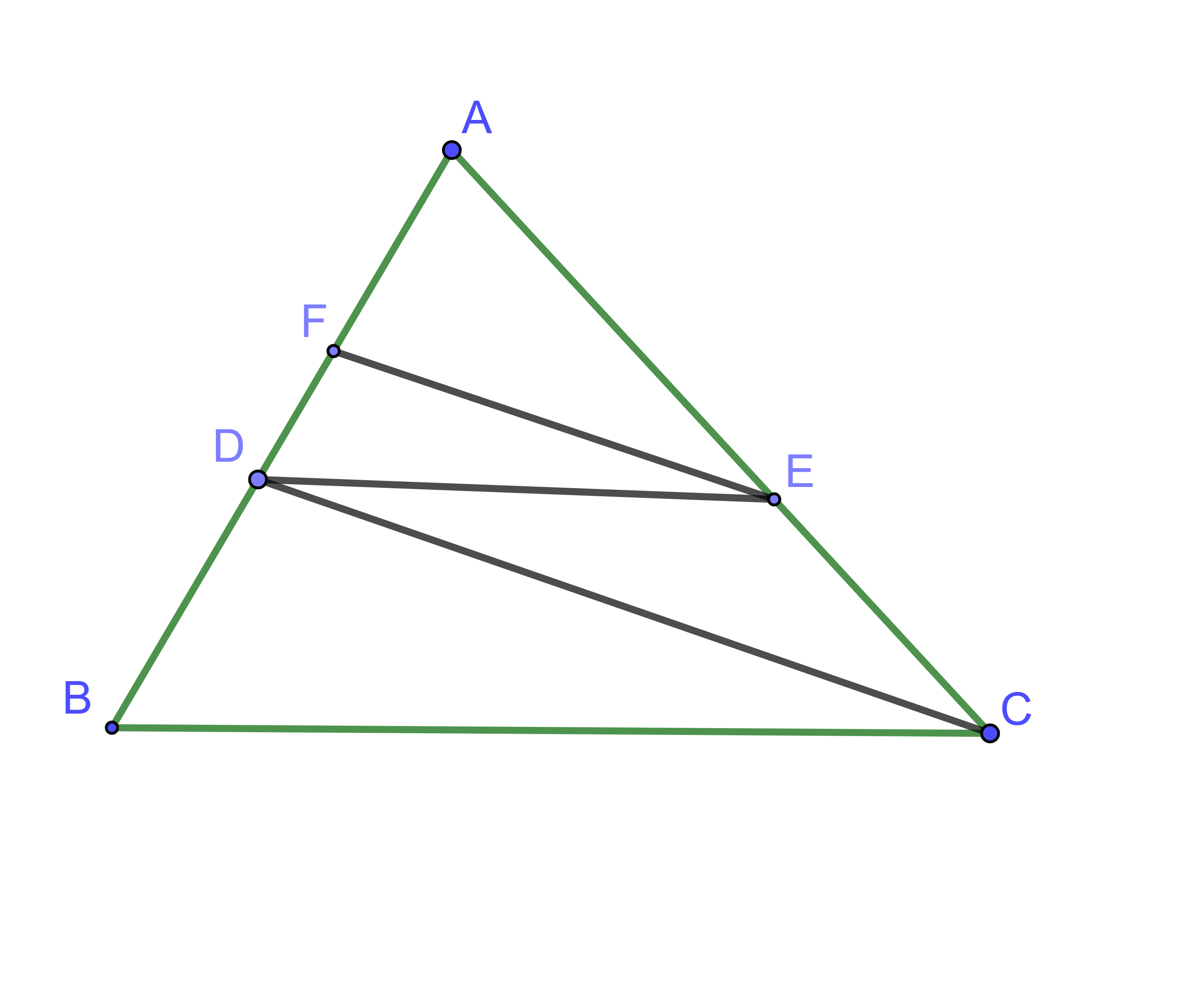
Với EF // CD, áp dụng định lý Thales ta có:
Với DE // BC, áp dụng định lý Thales ta có:
Cho tam giác ABC có trọng tâm G. Kẻ một đường thẳng bất kì qua G cắt cạnh AB, AC lần lượt tại M; N. Tính giá trị biểu thức ![]() .
.
Hình vẽ minh họa
Gọi AI là trung tuyến của tam giác ABC, vẽ
Ta có
Xét tam giác IBD và tam giác ICE có:
(đối đỉnh)
(AI là trung tuyến)
Trong tam giác AMG có nên
(theo định lí Thales)
Trong tam giác ANG có nên
(theo định lí Thales)
Khi đó:
Vì (cmt);
(G là trong tâm)
Vậy
Cho hình vẽ:
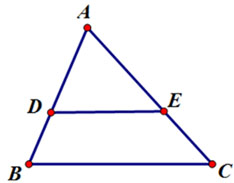
Điều kiện nào sau đây không suy ra được DE // BC?
Theo định lý đảo của định lý Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Dễ thấy, từ các điều kiện
Vậy đáp án cần tìm là .
Cho hình vẽ. Tìm x (làm tròn kết quả đến chữ thập phân thứ hai)
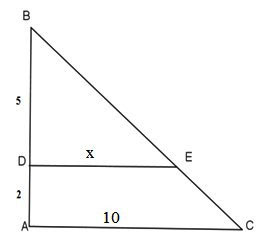
Ta có:
Vì , áp dụng hệ quả của định lý Thales, ta có:
Cho hình vẽ:
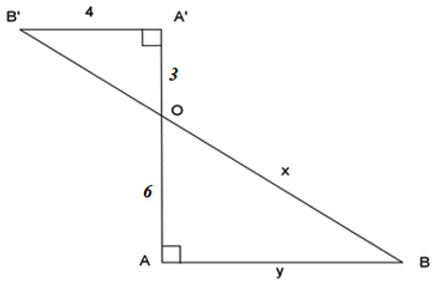
Giá trị biểu thức ![]() là:
là:
Áp dụng định lý Pythagore cho tam giác vuông , ta có:
Lại có:
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Thales, ta có:
Vậy
Cho tam giác ABC, lấy các điểm D, E lần lượt nằm trên cạnh BC và AD sao cho ![]() ,
, ![]() . Gọi K là giao điểm của BE với AC. Tính tỉ số
. Gọi K là giao điểm của BE với AC. Tính tỉ số ![]()
Hình vẽ minh họa
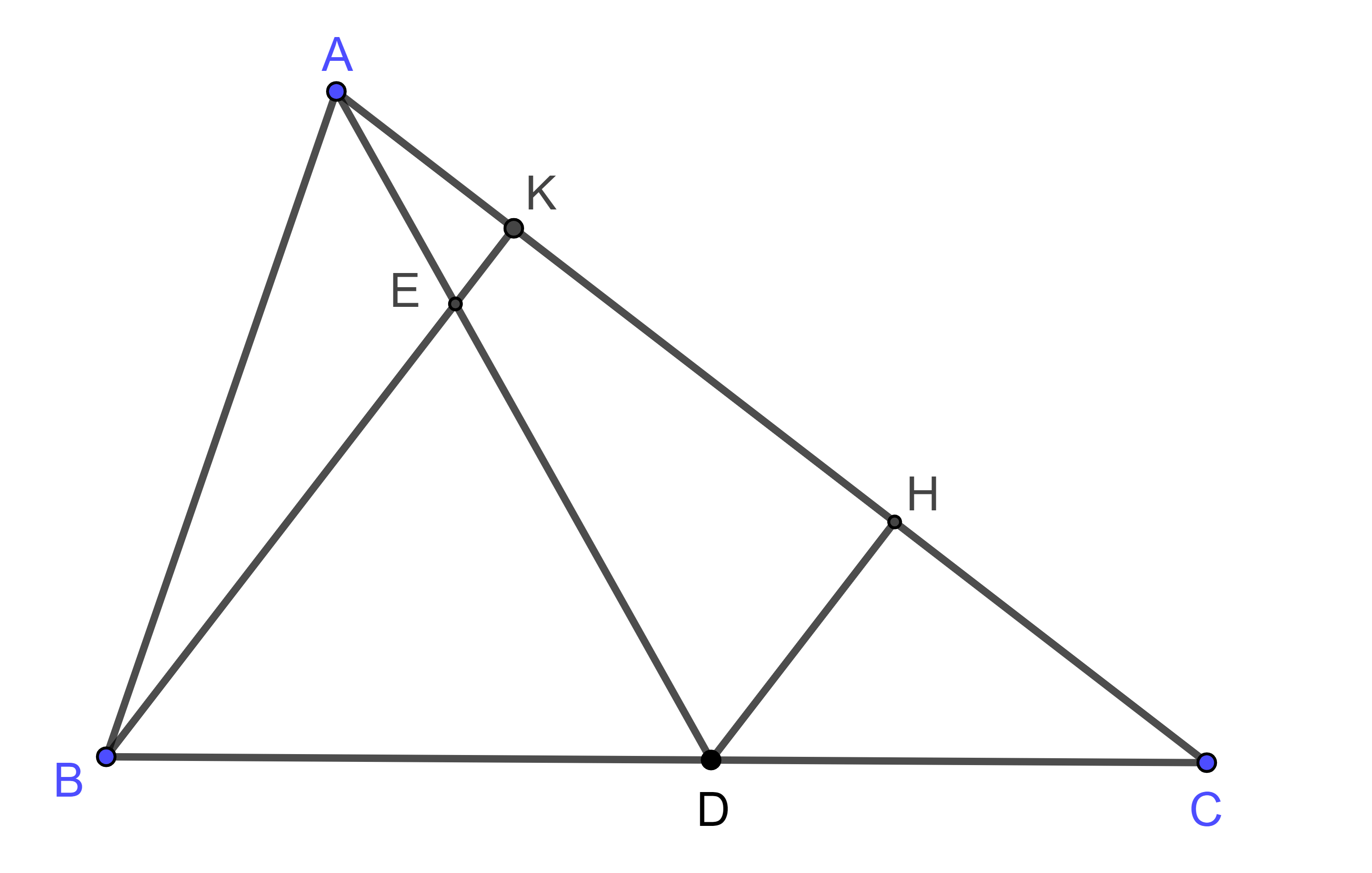
Qua D kẻ đường thẳng song song với BK cắt AC ở H.
Theo định lý Thales:
Do =>
Do =>
Từ (1) và (2) suy ra:
Vậy
Cho hình bình hành ABCD. Lấy điểm F là trung điểm của BC, điểm E thuộc cạnh AB sao cho ![]() . Gọi giao điểm của AC với các đường thẳng DE và DF lần lượt là I, K. Tính độ dài cạnh IK, biết độ dài cạnh AC là
. Gọi giao điểm của AC với các đường thẳng DE và DF lần lượt là I, K. Tính độ dài cạnh IK, biết độ dài cạnh AC là ![]() .
.
Hình vẽ minh họa
Ta có:
Ta có:
(Theo định lí Thales)
Do đó:
Ta lại có:
Do đó:
Cho tam giác ABC, AB < AC như hình vẽ:

Chọn khẳng định đúng.
Theo định lý đảo của định lý Thales:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ![]() có diện tích là
có diện tích là ![]() , kẻ AH vuông góc với BC. Trên cạnh AH lấy các điểm K và I sao cho
, kẻ AH vuông góc với BC. Trên cạnh AH lấy các điểm K và I sao cho ![]() . Từ điểm I, K lần lượt kẻ các đường thẳng
. Từ điểm I, K lần lượt kẻ các đường thẳng ![]() với
với ![]() . Khi đó diện tích tứ giác
. Khi đó diện tích tứ giác ![]() bằng bao nhiêu?
bằng bao nhiêu?
Kết quả: 30 ![]()
Cho tam giác có diện tích là
, kẻ AH vuông góc với BC. Trên cạnh AH lấy các điểm K và I sao cho
. Từ điểm I, K lần lượt kẻ các đường thẳng
với
. Khi đó diện tích tứ giác
bằng bao nhiêu?
Kết quả: 30
Hình vẽ minh họa
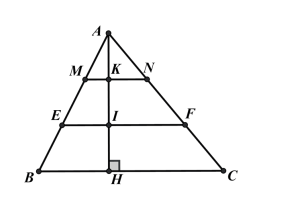
Ta có:
Xét tứ giác có
và
.
Do đó là hình thang có 2 đáy MN, FE, chiều cao KI.
Trong hình vẽ dưới đây có bao nhiêu cặp đường thẳng song song?
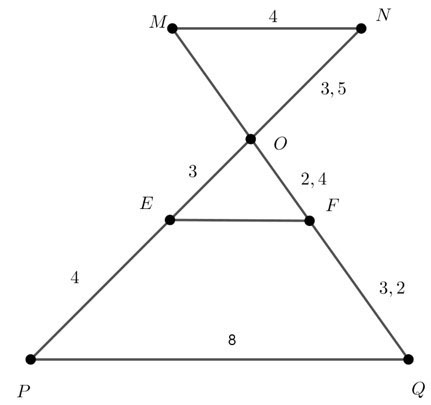
Ta có:
(theo định lí Thales đảo) (1)
Ta có:
(theo định lí Thales đảo) (2)
Từ (1) và (2) =>
Vậy có ba đường thẳng song song với nhau
Cho tam giác ![]() . Kẻ một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua điểm C kẻ đường thằng Cx song song với AB, cắt DE tại G. Khẳng định nào dưới đây đúng?
. Kẻ một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua điểm C kẻ đường thằng Cx song song với AB, cắt DE tại G. Khẳng định nào dưới đây đúng?
Hình vẽ minh họa
Tứ giác có
nên tứ giác
là hình bình hành
Trong tam giác nên
Từ (1) và (2) suy ra
Cho tam giác ABC, trọng tâm G. Qua G kẻ đường thẳng song song với AB và AC lần lượt cắt các cạnh BC và AC tại D và E.
Khi đó giá trị biểu thức ![]() 0
0
Cho tam giác ABC, trọng tâm G. Qua G kẻ đường thẳng song song với AB và AC lần lượt cắt các cạnh BC và AC tại D và E.
Khi đó giá trị biểu thức 0
Hình vẽ minh họa
Vì G là trong tâm tam giác ABC nên ta có:
Áp dụng định lí Thales vào tam giác MAB với DG//BA ta có:
Áp dụng định lí Talet vào tam giác MAC với GE//AC ta có:
Từ (*) và (**) suy ra:
Cho hình thang ![]() có diện tích 36cm2,
có diện tích 36cm2, ![]() . Gọi O là giao điểm của hai đường chéo. Kẻ
. Gọi O là giao điểm của hai đường chéo. Kẻ ![]() tại
tại ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Hình vẽ minh họa
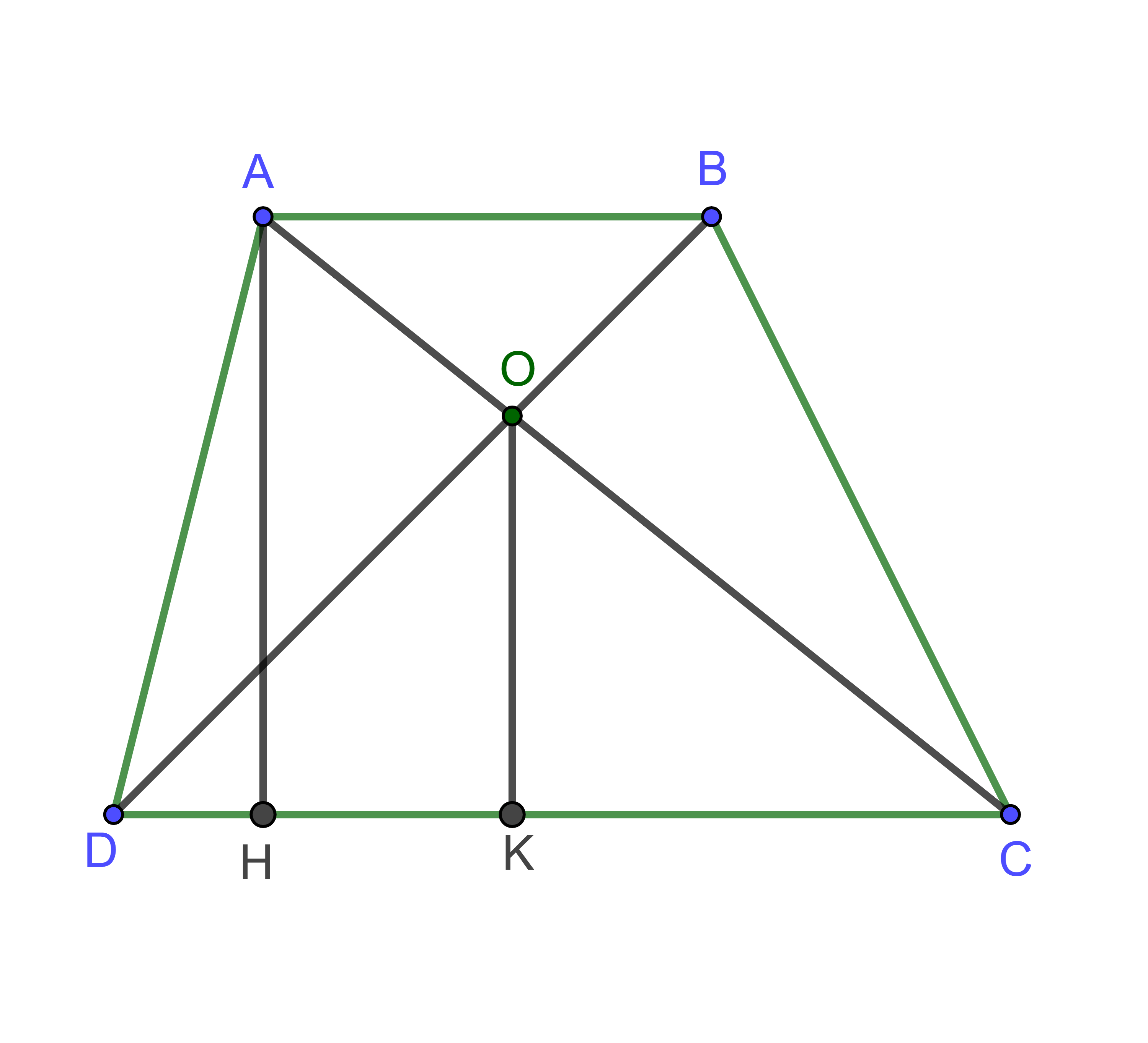
Ta có: tại
Chiều cao của hình thang:
Vì (do ABCD là hình thang) nên theo định lý Thales ta có
Vì (chứng minh trên) nên theo định lý Thales cho tam giác AHC ta có:
