Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Chọn câu đúng nhất.
Vì (giả thiết)
=> (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên
=> ABCD là hình thang (dấu hiệu nhận biết)
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Chọn câu đúng nhất.
Vì (giả thiết)
=> (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên
=> ABCD là hình thang (dấu hiệu nhận biết)
Nếu tam giác ABC có ![]() (với
(với ![]() ) thì
) thì
Vì MN // BC,
=> Tam giác AMN đồng dạng với tam giác ABC
Hay
Cho tứ giác ABCD có AB = 2cm, AD = 3cm, CD = 8cm và đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Khi đó các độ dài BD, BC bằng bao nhiêu?
Ta có:
Biết ![]() theo tỉ số m. Chọn kết luận sai dưới đây.
theo tỉ số m. Chọn kết luận sai dưới đây.
Ta có:
Tam giác ABC đồng dạng với tam giác MNP theo tỉ số ![]() , biết chu vi của tam giác ABC bằng 30 cm. Chu vi của tam giác MNP là:
, biết chu vi của tam giác ABC bằng 30 cm. Chu vi của tam giác MNP là:
Tam giác ABC có chu vi 30cm đồng dạng với tam giác MNP khi đó ta có:
Ta có ![]() thì
thì
Ta có:
=>
Cho ![]() như hình vẽ.
như hình vẽ.
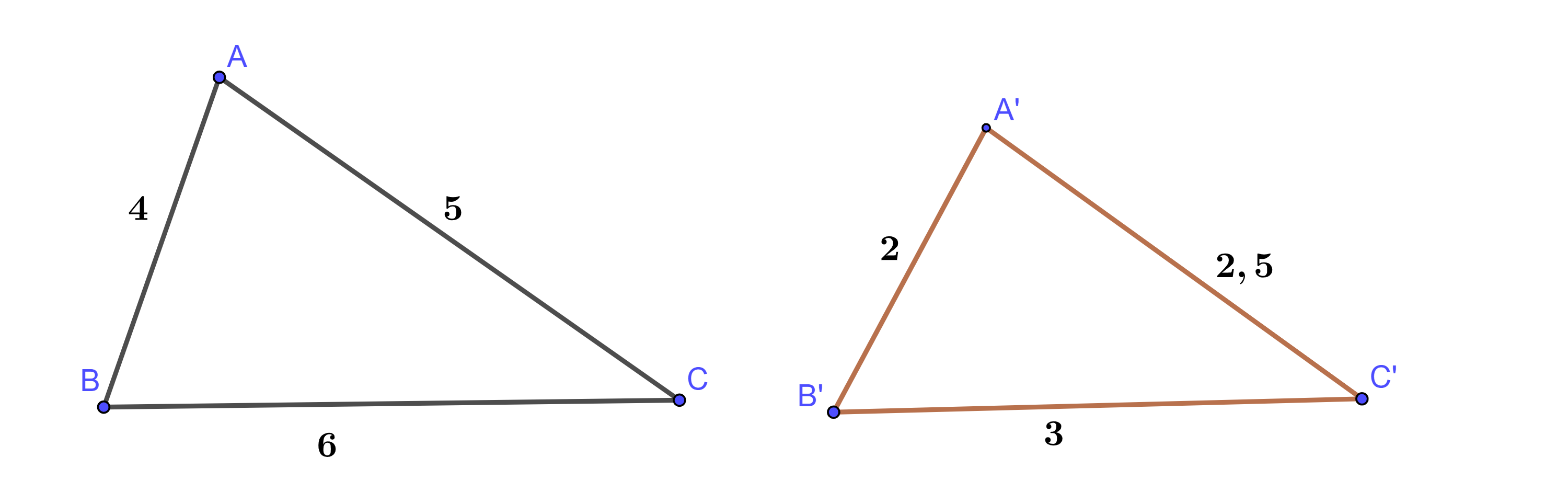
Tính tỉ số đồng dạng?
Kết quả: 1/2
(Kết quả ghi dưới dạng phân số tối giản a/b)
Cho như hình vẽ.

Tính tỉ số đồng dạng?
Kết quả: 1/2
(Kết quả ghi dưới dạng phân số tối giản a/b)
Ta có .
Khi đó tỉ số đồng dạng là
Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số ![]() . Biết
. Biết ![]() . Tính chu vi của tam giác
. Tính chu vi của tam giác ![]() .
.
Ta có:
Tam giác ABC đồng dạng với tam giác MNP theo tỉ số nên
Hãy chọn câu sai
Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1.
Hai tam giác đều có các góc đều bằng 600 và các cạnh tương ứng tỉ lệ nên chúng đồng dạng.
Hai tam giác vuông chưa chắc đồng dạng (chưa đủ dữ liệu về cạnh và góc tương ứng)
=> Đáp án sai là: "Hai tam giác vuông luôn đồng dạng với nhau".
Biết ![]() có
có ![]() . Chọn đáp án chính xác.
. Chọn đáp án chính xác.
Ta có:
Cho ![]() có
có ![]() . Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?
. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?
Ta có: Δ ABC ∼ Δ A'B'C'
(*)
Mặt khác (**)
Từ (*) và (**) ta có hệ phương trình:
Biết tam giác ABC có chu vi 40cm đồng dạng với tam giác MNP theo tỉ số ![]() . Tính chu vi tam giác MNP.
. Tính chu vi tam giác MNP.
Tam giác ABC có chu vi 40cm đồng dạng với tam giác MNP khi đó ta có:
Cho tam giác ABC và hai điểm M, N lần lượt thuộc các cạnh BC, AC sao cho ![]() . Chọn kết luận đúng.
. Chọn kết luận đúng.
Vì MN // AB và M, N lần lượt thuộc các cạnh BC, AC
=>Tam giác CMN đồng dạng với tam giác CBA hay
