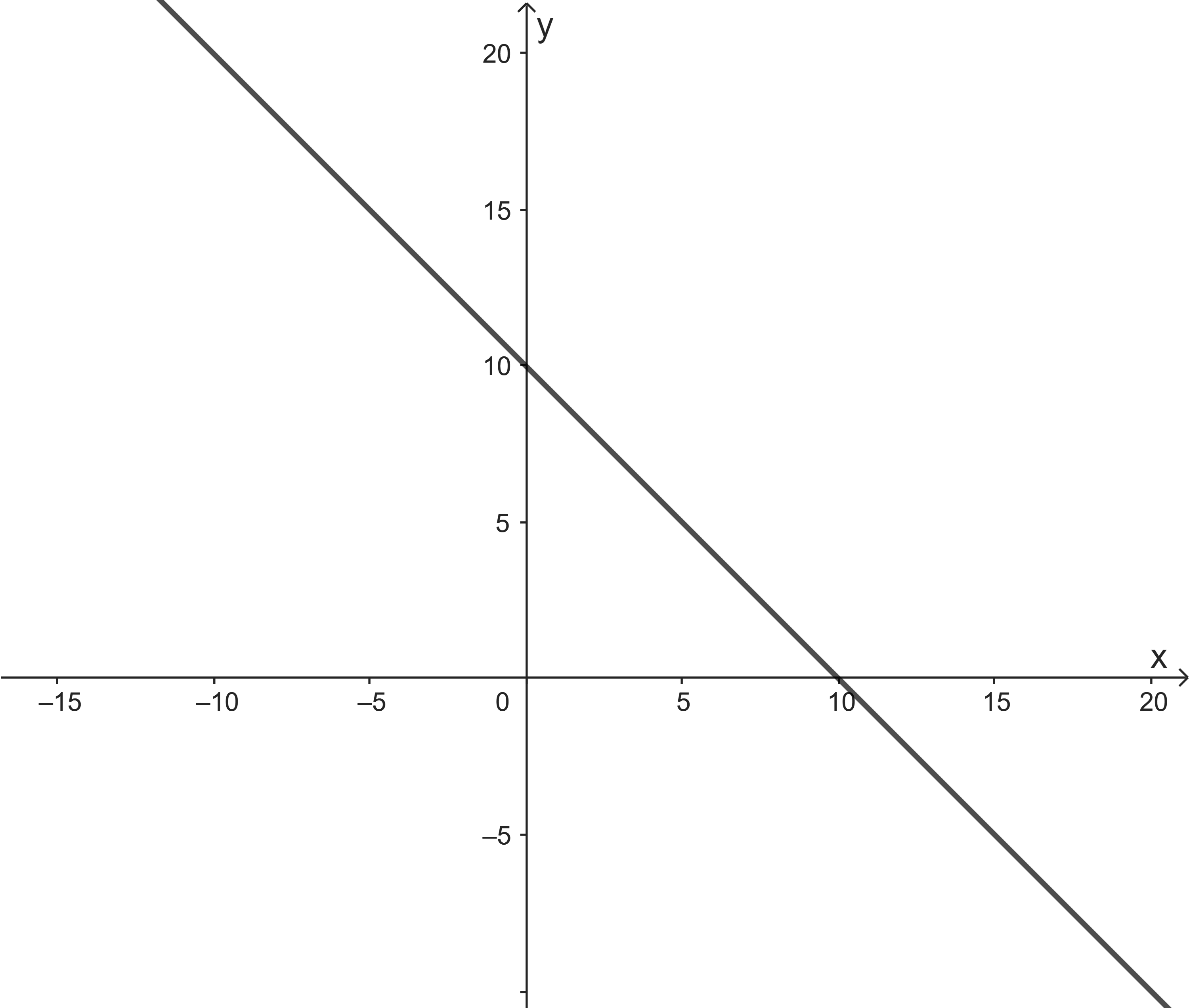Cho hàm số ![]() . Xác định a và b để hàm số đã cho là hàm số bậc nhất?
. Xác định a và b để hàm số đã cho là hàm số bậc nhất?
Để hàm số đã cho là hàm bậc nhất thì:
Từ (*) suy ra
Với thay (**) ta được
Với thay (**) ta được
Vậy để hàm số đã cho là hàm số bậc nhất thì hoặc
.
Cho hàm số ![]() . Xác định a và b để hàm số đã cho là hàm số bậc nhất?
. Xác định a và b để hàm số đã cho là hàm số bậc nhất?
Để hàm số đã cho là hàm bậc nhất thì:
Từ (*) suy ra
Với thay (**) ta được
Với thay (**) ta được
Vậy để hàm số đã cho là hàm số bậc nhất thì hoặc
.
Một người đi xe đạp từ A đến B xuất phát từ 6h với vận tốc không đổi 40km/h. Lúc 9 giờ một người đi xe máy đi từ A đến B với vận tốc không đổi 80km/h. Hỏi lúc x giờ (x > 9) trước khi hai xe gặp nhau thì khoảng cách y giữa hai xe là bao nhiêu km?
Thời gian xe đạp đi được là (giờ)
=> Quãng đường xe đạp đi được là (km)
Thời gian xe máy đi được là (giờ)
=> Quãng đường xe máy đi được là: (km)
Vậy khoảng cách giữa hai xe là:
Trong các điểm ![]() , điểm nào thuộc đồ thị hàm số
, điểm nào thuộc đồ thị hàm số ![]() ?
?
Thay toạ độ các điểm đã cho vào hàm số ta thấy điểm thuộc đồ thị hàm số vì
.
Tìm điểm ![]() cố định mà đường thẳng
cố định mà đường thẳng ![]() luôn đi qua với mọi giá trị của tham số m?
luôn đi qua với mọi giá trị của tham số m?
Ta có: là điểm cố định thuộc đồ thị hàm số, khi đó:
Vậy điểm cố định cần tìm là .
Tìm điều kiện để hàm số ![]() là hàm số bậc nhất?
là hàm số bậc nhất?
Để hàm số đã cho là hàm số bậc nhất thì
Cho hàm số bậc nhất ![]() . Tính giá trị của y khi
. Tính giá trị của y khi ![]() ?
?
Thay vào hàm số
ta được:
Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
Hàm số bậc nhất có dạng .
Cho hàm số ![]() . Tìm điều kiện để hàm số đã cho là hàm số bậc nhất?
. Tìm điều kiện để hàm số đã cho là hàm số bậc nhất?
Điều kiện để hàm số đã cho là hàm số bậc nhất là:
Điểm nào sau đây không thuộc đồ thị hàm số ![]() ?
?
Thay tọa độ các điểm vào hàm số ta thấy điểm không thuộc đồ thị hàm số đã cho vì
.
Hoàn thành bảng sau:
x | -2 | -1 | 0 | 3 | -4 |
-5 | -3 | -1 | 5 | -9 | |
8 | 5 | 2 | -7 | 14 |
Hoàn thành bảng sau:
x | -2 | -1 | 0 | 3 | -4 |
-5 | -3 | -1 | 5 | -9 | |
8 | 5 | 2 | -7 | 14 |
Hoàn thành bảng như sau:
x | -2 | -1 | 0 | 3 | -4 |
-5 | -3 | -1 | 5 | -9 | |
8 | 5 | 2 | -7 | 14 |
Cho hàm số ![]() . Xác định giá trị m để đồ thị hàm số đi qua điểm
. Xác định giá trị m để đồ thị hàm số đi qua điểm ![]() ?
?
Do đồ thị hàm số đi qua điểm nên thay
vào hàm số ta được:
Vậy m = 0.
Điểm ![]() nằm trên đường thẳng nào?
nằm trên đường thẳng nào?
Vì nên điểm M nằm trên đường thẳng
.
Cho hàm số ![]() . Xác định a và b biết rằng đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -4 và cắt trục hoành tại điểm có hoành độ bằng 1?
. Xác định a và b biết rằng đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -4 và cắt trục hoành tại điểm có hoành độ bằng 1?
Giao điểm của đồ thị với trục tung là A(0,−4), với trục hoành là B(1,0).
Ta có:
Hàm số nào sau đây không phải là hàm số bậc nhất với mọi giá trị của tham số m?
Xét ta có:
nên hàm số luôn là hàm số bậc nhất.
Xét ta có:
nên hàm số luôn là hàm số bậc nhất.
Xét ta có:
nên hàm số luôn là hàm số bậc nhất.
Xét là hàm phân thức nên không phải là hàm số bậc nhất.
Xác định đồ thị hàm số ![]() ?
?
Đồ thị hàm số được biểu diễn như sau: